Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika IPA
Vektor
MATERI
Perkalian Skalar Dua Vektor dan Proyeksi Vektor
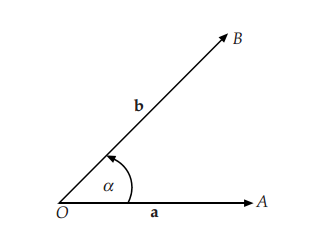
Jika a dan b vektor-vektor tak nol dan 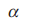 sudut di antara vektor a dan b, maka perkalian skalar vektor a dan b didefinisikan oleh a . b = |a | |b| cos
sudut di antara vektor a dan b, maka perkalian skalar vektor a dan b didefinisikan oleh a . b = |a | |b| cos  .
.
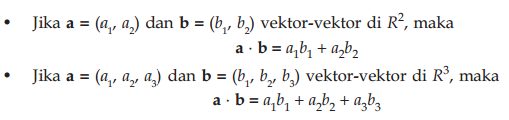
Misalkan a1, a2 dan a3 adalah bilangan-bilangan positip dan diketahui persamaan vektor a = a1i+ a2j + a3k, maka panjang vektor a secara geometris dapat digambarkan :
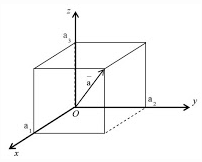
Dengan bantuan teorema Pythagoras dapat ditentukan panjang vektor a , yaitu:
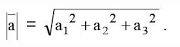
Sedangkan untuk A(Ax, Ay, Az) dan B(Bx, By, Bz) maka panjang vektor AB dirumuskan :
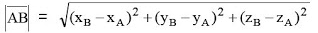
Sebagai contoh, misalkan vector a = 4 i – 5 j + 3 k , maka panjang vector a adalah :
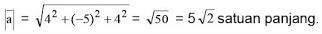
Sedangkan untuk titik A(-2, 4, -1) dan B(-5, 2, 5), maka panjang vektor AB didapat:
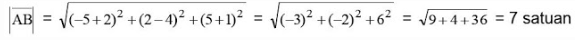
Jika a = a1i+ a2j + a3k dan b = b1i+ b2j + b3k maka perkalian skalar a dan b secara geometris didefinisikan:

Sebagai contoh diketahui dua vector a dan b seperti gambar berikut.
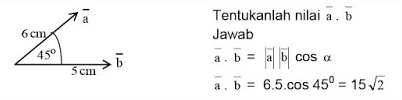
Sedangkan secara analitis perkalian skalar dua vektor a dan b didapat dengan cara:
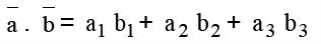
1.
Diketahui dua vektor a dan b seperti berikut
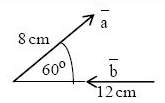
Tentukanlah nilai a . b
A. -48
B. 48
C. -84
D. 84
E. -88
JAWABAN BENAR
A.
-48
PEMBAHASAN
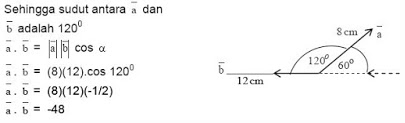
2. Diketahui P(2, 2x, 0), Q(–1, 1, –7) dan R(3x, 3, x). Jika PQ . PR = –23 maka tentukanlah nilai x
A. x = 2 atau x= 4
B. x=2 atau x= 8
C. x=-2 atau x=8
D. x=-2 atau x=-8
E. x=-4 atau x=2
JAWABAN BENAR
A.
x = 2 atau x= 4
PEMBAHASAN
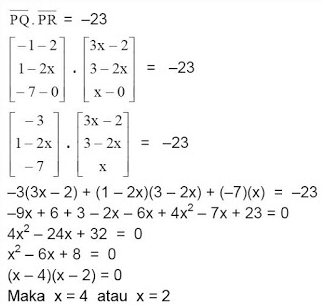

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

