Belajar Pintar Materi SMP, SMA, SMK
BelajarPintarV3
Matematika
Himpunan
MATERI
Irisan (Intersection)

Irisan adalah dua himpunan yang bagian-bagiannya menjadi anggota dari keduanya. Gabungan adalah dua himpunan yang anggotanya hanya bilangan itu saja misalnya anggota bilangan A saja, anggota bilangan B saja dan anggota A, B keduanya.
Untuk lebih memahami apa itu irisan dan gabungan dari dua himpunan, coba amati hubungan dua himpunan dalam tabel berikut ini. Fokuskan pengamatan kalian pada irisan dari dua himpunan.
Tabel Irisan dan Gabungan dari Dua Himpunan
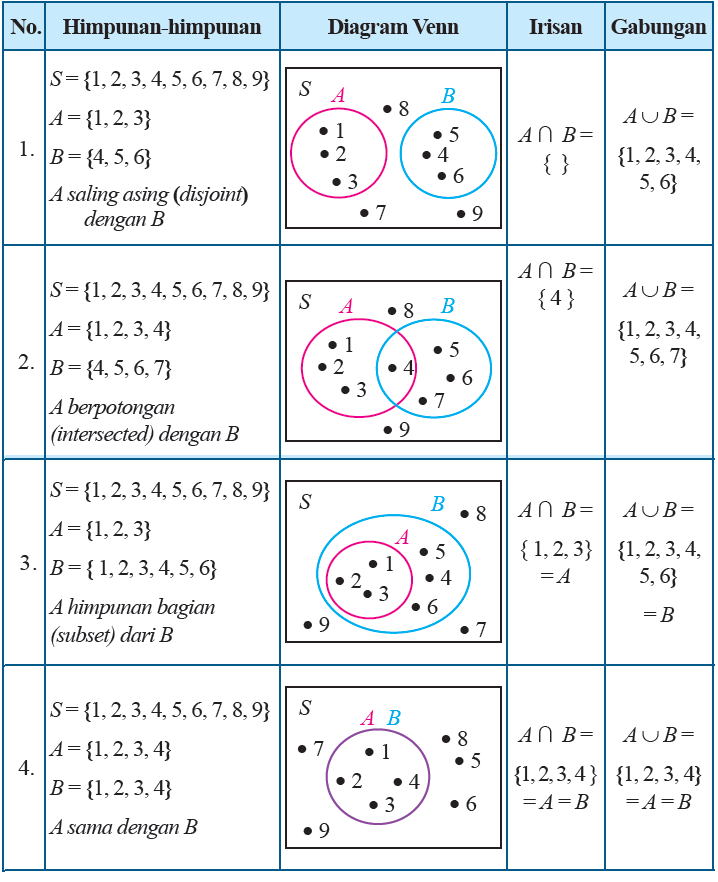
1. Misalkan S adalah himpunan semesta, irisan himpunan A dan B adalah himpunan yang anggotanya semua anggota S yang merupakan anggota himpunan A dan anggota himpunan B, dilambangkan dengan Irisan dua himpunan dinotasikan
2. Misalkan S adalah himpunan semesta, gabungan himpunan A dan B adalah himpunan yang anggotanya semua anggota S yang merupakan anggota himpunan A atau anggota himpunan B, dilambangkan denganGabungan dua himpunan ditulis
Gabungan (Union)

Gabungan dalam teori himpunan merupakan operasi penggabungan dua himpunan, sehingga menghasilkan himpunan baru yang berisi anggota-anggota kedua himpunan awal. Operasi penggabungan himpunan (union dalam bahasa Inggris) dilambangkan dengan tanda .
Untuk lebih memahami tentang gabungan, mari Sobat Pintar simak contoh soal dibawah ini:
Contoh Soal :
Diketahui himpunan A = {1, 3, 5, 7) dan B = {5, 7, 8, 9, 10}.
a. Gambarlah diagram Venn dari kedua himpunan tersebut
b. Tentukan
Penyelesaian :
a. Kedua himpunan itu adalah:
A = {1, 3, 5, 7)
B = {5, 7, 8, 9, 10}
Diagram Venn dari kedua himpunan tersebut adalah
b. = {1, 3, 5, 7, 8, 9, 10}
Komplemen (Complement)

Gabungan, Irisan, dan Selisih adalah contoh dari operasi biner, yaitu operasi yang memerlukan dua unsur untuk dioperasikan. Selain operasi biner ada operasi uner yang hanya memerlukan satu unsur, yaitu operasi komplemen. Berbeda dengan operasi biner yang semestanya tidak perlu ditetapkan, maka operasi komplemen memerlukan ditetapkannya himpunan semesta. Tanpa himpunan semesta, operasi komplemen ini tidak bisa dilakukan. Sebenarnya operasi komplemen ini mirip dengan operasi selisih, hanya saja yang dicari adalah selisih dari semesta dari himpunan tertentu.
Misalkan S adalah himpunan semesta dan A adalah suatu himpunan.
1. Komplemen himpunan A adalah suatu himpunan semua anggota himpunan S yang bukan anggota himpunan A, dinotasikan dengan Ac.
Notasi pembentuk himpunan 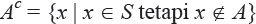
2. Selisih himpunan B terhadap himpunan A adalah himpunan semua anggota himpunan A yang bukan anggota himpunan B, dinotasikan dengan A - B.
Notasi pembentuk himpunan 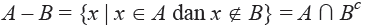
Tabel Komplemen dan Selisih Himpunan
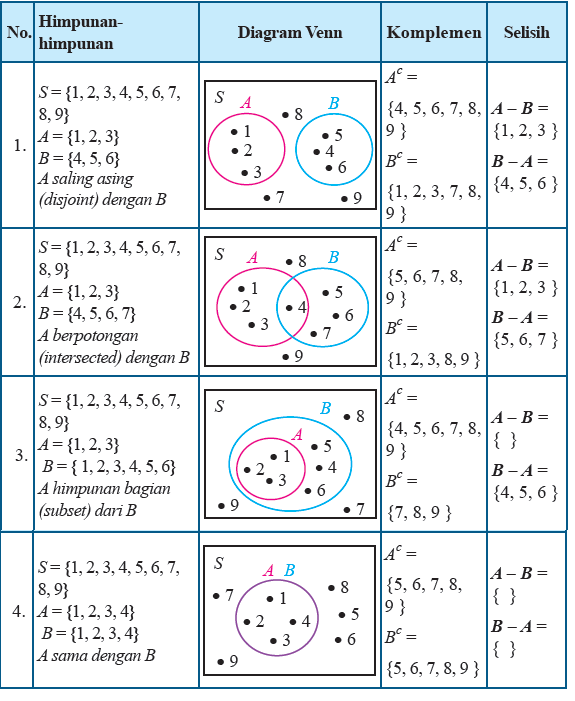
Selisih (Difference)

Selisih (difference) himpunan A dan B adalah himpunan yang anggotanya semua anggota dari A tetapi bukan anggota dari B.
Sobat Pintar, untuk lebih memahami apa itu selisih, mari kita simak contoh soal dibawah ini
Contoh Soal :
Dalam suatu kelas terdapat 30 orang siswa yang senang dengan pelajaran matematika, 25 orang siswa senang dengan pelajaran fisika, dan 10 orang siswa senang pelajaran matematika dan fisika.
a. Gambarlah diagram Venn dari keterangan di atas.
b. Berapa orang siswa yang hanya senang pelajaran matematika?
c. Berapa orang siswa yang hanya senang pelajaran fisika?
d. Berapa banyak siswa dalam kelas itu?
Penyelesaian :
Pada masalah ini, tidak disajikan anggota-anggota setiap himpunan, cukup kita fokus pada banyak anggota setiap himpunan. Perlu kalian ketahui bahwa siswa yang senang dengan pelajaran matematika tidak menutup kemungkinan bahwa siswa tersebut juga senang dengan pelajaran fisika, sebaliknya juga demikian. Misalkan A adalah himpunan semua siswa yang senang belajar matematika, maka n(A) = 30. Misalkan B adalah himpunan semua siswa yang senang belajar fisika, maka n(B) = 25.
Misalkan M adalah himpunan semua siswa yang hanya senang belajar matematika. Misalkan F adalah himpunan semua siswa yang hanya senang belajar fisika. Misalkan S adalah himpunan semua siswa dalam satu kelas. A irisan B adalah himpunan siswa senang pelajaran matematika dan fisika, maka n(A irisan B) = 10.
a. Diagram Venn
b. Siswa yang hanya senang pelajaran matematika
Banyak siswa yang senang pelajaran matematika adalah banyak siswa yang hanya senang belajar matematika ditambah dengan banyak siswa yang senang belajar kedua-duanya.
n(A) = n(M) + n(A irisan B)
30 = n(M) + 10
n(M) = 30 - 10
= 20
Maka banyak siswa yang hanya senang belajar matematika adalah 20 orang.
c. Siswa yang hanya senang pelajaran fisika.
Banyak siswa yang senang pelajaran fisika adalah banyak siswa yang hanya senang belajar fisika ditambah dengan banyak siswa yang senang belajar kedua-duanya.
n(B) = n(F) + n(A irisan B)
25 = n(F) + 10
n(F) = 25 - 10 = 15
Maka banyak siswa yang hanya senang belajar matematika adalah 15 orang.
d. Banyak siswa dalam kelas
Banyak siswa dalam satu kelas yaitu banyak siswa yang hanya senang belajar matematika ditambah dengan banyak siswa yang hanya senang belajar fisika ditambah dengan banyak siswa yang senang belajar keduaduanya.
n(S) = n(M) + n(F) + n(A irisan B)
= 20 + 15 + 10
= 45
Jadi, banyak siswa kelas itu adalah 45 orang.
Sifat-sifat Operasi Himpunan

a. Sifat Idempoten
Sifat idempoten adalah sifat dalam pengoperasian dua buah objek yg hasilnya objek itu sendiri.
Untuk lebih memahami sifat idempoten Sobat Pintar dapat menyimak contoh soal dibawah ini
Contoh Soal :
Anto memiliki olahraga kesukaan yaitu: sepak bola, bola voli, dan catur. Misalkan himpunan semua olahraga kesukaan Anto adalah himpunan K.
1. Hal apa yang kalian temukan jika himpunan olahraga kesukaan Anto digabung dengan himpunan olahraga kesukaannya sendiri?
2. Hal apa yang kalian temukan jika himpunan olahraga kesukaan Anto diiriskan dengan himpunan olahraga kesukaannya sendiri?
Penyelesaian :

b. Sifat Identitas
Sifat identitas merupakan sifat operasi suatu bilangan yang hasilnya bilangan itu sendiri
Untuk lebih memahami sifat identitas Sobat Pintar dapat menyimak contoh soal dibawah ini
Contoh Soal :
Budi dan Badu adalah siswa kelas VII SMP. Budi senang dengan pelajaran matematika, bahasa Indonesia, dan kimia. Sedangkan Badu tidak senang dengan pelajaran apa pun.
1. Jika pelajaran yang disenangi Budi dan Badu merupakan himpunan, tentukanlah anggota kedua himpunan itu.
2. Jika pelajaran yang disenangi Budi digabung dengan pelajaran yang disenangi Badu, apa yang kalian simpulkan?
3. Pelajaran apa yang sama-sama disenangi Budi dan Badu?
Misal: A adalah himpunan semua pelajaran yang disenangi Budi.
B adalah himpunan semua pelajaran yang disenangi Badu.
1. Kedua himpunan tersebut adalah
A = {matematika, bahasa Indonesia, kimia}
B adalah himpunan pelajaran yang disenangi Badu
B = { }
2. Himpunan semua pelajaran yang disenangi Budi digabung dengan
himpunan semua pelajaran yang disenangi Badu, dilambangkan dengan A ![]() B
B
A ![]() B = {matematika, bahasa Indonesia, kimia}
B = {matematika, bahasa Indonesia, kimia} ![]() { }
{ }
= {matematika, bahasa Indonesia, kimia}
ternyata A ![]() B = A
B = A
3. Himpunan semua pelajaran pelajaran yang sama-sama disenangi Budi
dan Badu, dilambangkan dengan A ![]() B.
B.
A ![]() B = {matematika, bahasa Indonesia, kimia}
B = {matematika, bahasa Indonesia, kimia} ![]() { }
{ }
= { }
Maka pelajaran yang sama-sama disenangi Budi dan Badu adalah tidak ada.
Berdasarkan penyelesaian masalah di atas, dapat disimpulkan bahwa
Untuk sebarang himpunan A, berlaku:
A ![]()
![]() = A
= A
A ![]()
![]() =
= ![]()
c. Sifat Komutatif
Sifat komutatif pada operasi himpunan hanya berlaku pada operasi irisan dan gabungan, yaitu A![]() B = B
B = B![]() A danA
A danA![]() B = B
B = B![]() A
A
Amati diagram Venn I dan II berikut ini
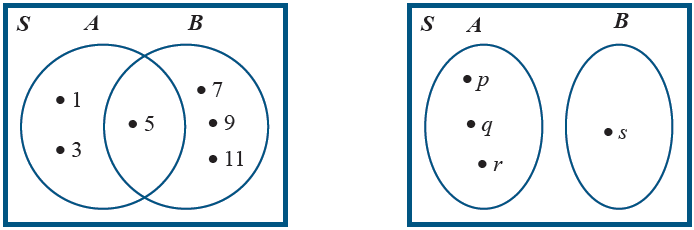
Diagram Venn I dan II
Dari diagram Venn I dan II tersebut diperoleh hal berikut
Diagram Venn I: Diagram Venn II:
A = {1, 3, 5} A = {p, q, r}
B = {5, 7, 9, 11} B = {s}
A ![]() B = {1, 3, 5, 7, 9, 11} A
B = {1, 3, 5, 7, 9, 11} A ![]() B = (p, q, r, s)
B = (p, q, r, s)
B ![]() A = {1, 3, 5, 7, 9, 11} B
A = {1, 3, 5, 7, 9, 11} B ![]() A = (p, q, r, s)
A = (p, q, r, s)
A ![]() B = {5} A
B = {5} A ![]() B =
B = ![]()
B ![]() A = {5} B
A = {5} B ![]() A =
A = ![]()
ternyata: ternyata:
A ![]() B = B
B = B ![]() A A
A A ![]() B = B
B = B ![]() A
A
A ![]() B = B
B = B ![]() A A
A A ![]() B = B
B = B ![]() A
A
Berdasarkan diagram Venn I dan II tersebut, maka dapat disimpulkan sebagai berikut
Misalkan A dan B adalah himpuan:
A ![]() B = B
B = B ![]() A
A
A ![]() B = B
B = B ![]() A
A
d. Sifat Asosiatif
Sifat asosiatif pada operasi himpunan hanya berlaku pada operasi irisan dan gabungan, yaitu (A![]() B)
B)![]() C = A
C = A![]() (B
(B![]() C) dan (A
C) dan (A![]() B)
B)![]() C = A
C = A![]() (B
(B![]() C)
C)
Perhatikan diagram Venn berikut.
Diagram Venn
Diperoleh:
P = {a, b, c, d, e}
Q = {d, e, f, g, h, i}
R = {c, e, i, j, k, l, m}
P ![]() Q = {a, b, c, d, e, f, g, h, i}
Q = {a, b, c, d, e, f, g, h, i}
Q ![]() R = {c, d, e, f, g, h, i, j, k, l, m}
R = {c, d, e, f, g, h, i, j, k, l, m}
(P ![]() Q)
Q) ![]() R = {a, b, c, d, e, f, g, h, i, j, k, l, m}
R = {a, b, c, d, e, f, g, h, i, j, k, l, m}
P ![]() (Q
(Q ![]() R) = {a, b, c, d, e, f, g, h, i, j, k, l, m}
R) = {a, b, c, d, e, f, g, h, i, j, k, l, m}
(P ![]() Q)
Q) ![]() R = {e}
R = {e}
P ![]() (Q
(Q ![]() R) = {e}
R) = {e}
Ternyata
(P ![]() Q)
Q) ![]() R = P
R = P ![]() (Q
(Q ![]() R)
R)
(P ![]() Q)
Q) ![]() R = P
R = P ![]() (Q
(Q ![]() R)
R)
e. Sifat Distributif
Sifat distributif pada operasi himpunan hanya berlaku pada operasi irisan dan gabungan, yaitu A![]() (B
(B![]() C) = (A
C) = (A![]() B)
B)![]() (A
(A![]() C) dan A
C) dan A![]() (B
(B![]() C)=(A
C)=(A![]() B)
B)![]() (A
(A![]() C).
C).
Dari diagram Venn diatas ditemukan juga :
P ![]() (Q
(Q ![]() R) = {a, b, c, d, e, i}
R) = {a, b, c, d, e, i}
(P ![]() Q)
Q) ![]() (P
(P ![]() R) = {a, b, c, d, e, i}
R) = {a, b, c, d, e, i}
P ![]() (Q
(Q ![]() R) = {c, d, e}
R) = {c, d, e}
(P ![]() Q)
Q) ![]() (P
(P ![]() R) = {c, d, e}
R) = {c, d, e}
Ternyata:
P ![]() (Q
(Q ![]() R) = (P
R) = (P ![]() Q)
Q) ![]() (P
(P ![]() R)
R)
P ![]() (Q
(Q ![]() R)= (P
R)= (P ![]() Q)
Q) ![]() (P
(P ![]() R)
R)
1.
Kerjakanlah Soal berikut ini dengan benar!
Diketahui himpunan A, B dan C masing-masing anggotanya sebagai berikut:
A = {2, 3, 5, 7, 11, 13}
B = {0, 2, 4, 6, 8, 10, 12}
C = {1, 2, 3, 4, 6, 12}
Tentukanlah (A irisan B) irisan C !
A. { }
B. { 0 }
C. {2}
D. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}
JAWABAN BENAR
C.
{2}
PEMBAHASAN
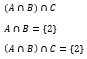
2.
Kerjakanlah Soal berikut ini dengan benar!
Diketahui :
P = {1, 3, 4, 5, 6, 7, 8, 9}
Q = {1, 3, 5, 7, 9}
P – Q = …
A. {1, 3, 5, 7, 9}
B. {4, 6, 8}
C. {1, 3, 4, 5, 6, 7, 8, 9}
D. {3, 4, 6, 9}
JAWABAN BENAR
B.
{4, 6, 8}
PEMBAHASAN
Selisih dari himpunan P dan himpunan Q adalah jumlah seluruh anggota P yang bukan anggota Q.
sehingga P – Q = {4, 6, 8}
3.
Kerjakanlah Soal berikut ini dengan benar!
Diketahui himpunan A dan C masing-masing anggotanya sebagai berikut:
A = {Bilangan Prima Kurang dari 10}
C = {Bilangan Ganjil Kurang dari 15}
Tentukanlah A gabungan C !
A. A gabungan C ={1,2,3,5,7,9,11,13,15,}
B. A gabungan C ={1,2,3,5,6,7,9,11,13}
C. A gabungan C ={1,2,3,4,5,6,7,8,9,11,13}
D. A gabungan C ={1,2,3,5,7,9,11,13}
JAWABAN BENAR
C.
A gabungan C ={1,2,3,4,5,6,7,8,9,11,13}
PEMBAHASAN
A = {Bilangan Prima Kurang dari 10}
C = {Bilangan Ganjil Kurang dari 15}
A={2,3,5,7}
C={1,3,5,7,9,11,13}
Maka A gabungan C adalah :
A gabungan C ={1,2,3,5,7,9,11,13}
4.
Kerjakanlah Soal berikut ini dengan benar!
Diketahui Himpunan A={x|0 < x <12, x elemen bilangan ganjil} dan B={x|x < 20 , x elemen bilangan prima}.Tentukan A irisan B?
A. { 1,3,5,7,11}
B. {3,5,7,11}
C. {1,3,5,7,9,11}
D. {0,1,2,3,4,5,6,7,8,9,10,11,12,13}
JAWABAN BENAR
B.
{3,5,7,11}
PEMBAHASAN
A={x|0 < x <12, x elemen bilangan ganjil}
B={x|x < 20 , x elemen bilangan prima}
A={1,3,5,7,9,11}
B={2,3,5,7,11,13,17,19}
A irisan B= {3,5,7,11}

Oops!!!
Yah, jawaban kamu meleset nih. Ingin melihat pembahasan soal ini?

BENAR!!!
Selamat!
Jawaban kamu benar. Ingin lihat pembahasan soal ini?
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved

