Materi Matematika - Transformasi Geometri Kelas Persiapan SBMPTN - Belajar Pintar
BelajarPintarV3
Translasi
Perpindahan suatu semua titik sejauh jarak yang sama dalam satu arah. Bentuk Umumnya adalah :
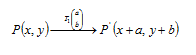
Jika digambarkan, maka translasi adalah sebagai berikut :
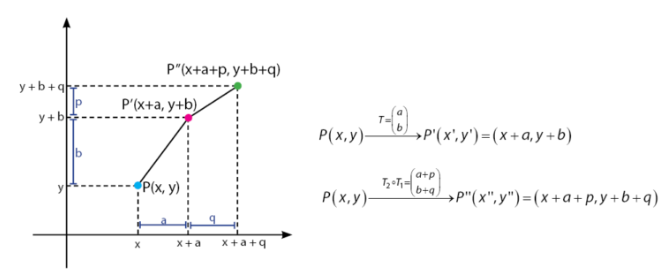
Bagaimana nih sobat pintar, sudah faham belum dengan materi yang telah di sampaikan ? yuk kita diskusikan bersama sobat pintar lainnya
B(3,5). Tentukan koordinat bayangan segitiga OAB tersebut bila ditranslasi oleh 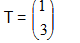
penyelesaian :
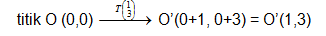
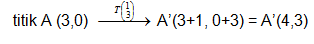
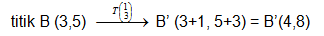
mudah kan sobat pintar?
Refleksi
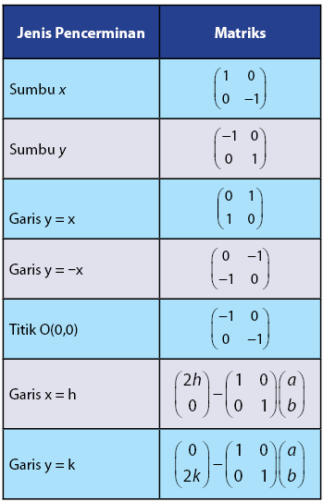
Pembahasan berikutnya adalah pencerminan atau yang lebih sering disebut dengan refleksi. Seperti halnya bayangan benda yang terbentuk dari sebuah cermin. Sebuah objek yang mengalami refleksi akan memiliki bayangan benda yang dihasilkan oleh sebuah cermin. Hasil dari refleksi dalam bidang kartesius tergantung sumbu yang menjadi cerminnya. Pembahasan materi refleksi yang akan diberikan ada tujuh jenis. Jenis-jenis tersebut antara lain adalah refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k. Berikut ini adalah ringkasan daftar matriks transformasi pada refleksi/pencerminan.
Rotasi
Rotasi atau perputaran merupakan perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu. Besarnya rotasi dalam transformasi geometri sebesar 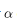 disepakati untuk arah yang berlawanan dengan arah jalan jarum jam. Jika arah perputaran rotasi suatu benda searah dengan jarum jam, maka sudut yang dibentuk adalah -
disepakati untuk arah yang berlawanan dengan arah jalan jarum jam. Jika arah perputaran rotasi suatu benda searah dengan jarum jam, maka sudut yang dibentuk adalah -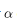 . Hasil rotasi suatu objek tergantung dari pusat dan besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar
. Hasil rotasi suatu objek tergantung dari pusat dan besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar 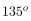 dengan pusat O (0,0) pada gambar di bawah
dengan pusat O (0,0) pada gambar di bawah
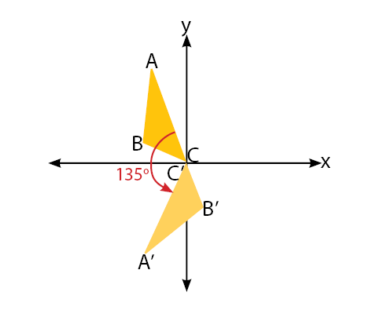
Mendapatkan hasil rotasi dengan cara menggambarnya terlebih dahulu akan sangat tidak efektif. Ada cara lain yang dapat digunakan untuk menentukakn hasil objek hasil rotasi, yaitu dengan menggunakan rumus transformasi geometri untuk rotasi. Untuk lebih lanjut kita akan bahas satu per satu rumus rumus yang ada di rotasi
Dilatasi
Dilatasi disebut juga dengan perbesaran atau pengecilan suatu objek. Jika transformasi pada translasi, refleksi, dan rotasi hanya mengubah posisi benda, maka dilatasi melakukan transformasi geometri dengan merubah ukuran benda. Ukuran benda dapat menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi faktor pengalinya. Rumus dalam dilatasi ada dua, yang dibedakan berdasarkan pusatnya.
Materi Matematika SMA - Persiapan SBMPTN Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








