Materi Matematika Minat - Fungsi Eksponen dan Logaritma Kelas 10 MIA

APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Peta Belajar Bersama

Hai, Sobat Pintar!
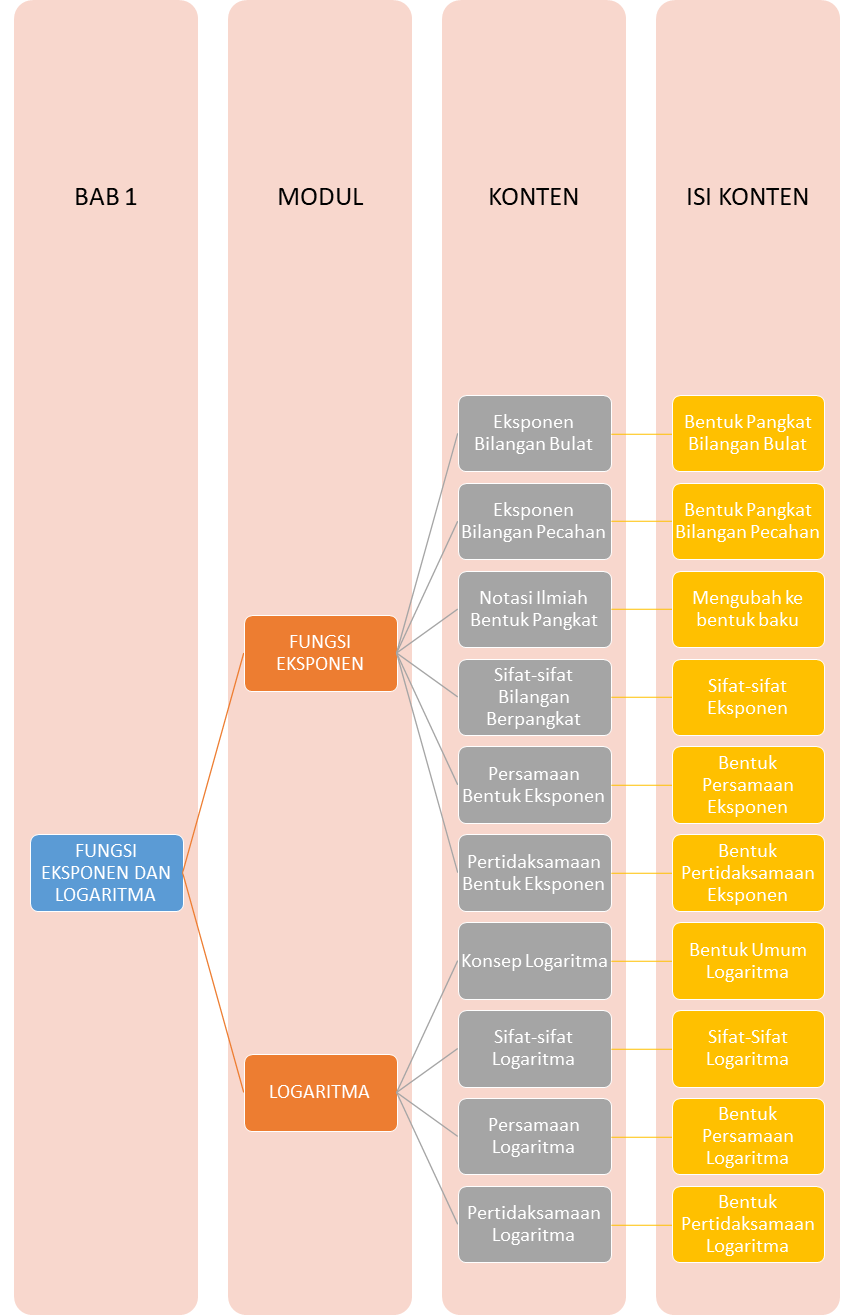
Sebelum sobat belajar tentang materi Eksponen dan Logaritma, yuk disimak peta belajar bersama berikut ini dulu, ya!

Eksponen Bilangan Bulat

Halo, Sobat Pintar! Kalian pasti sudah tahu mengenai bilangan berpangkat, bukan?

Nah! Materi kali ini adalah materi lanjutan dari materi pangkat sebelumnya, Sobat!

Simak penjelasannya baik-baik, ya!

Pangkat yang disebut juga sebagai Eksponen merupakan perkalian berulang dari sebuah bilangan real. Bilangan yang berpangkat bulat meliputi bilangan dengan pangkat bulat positif, pangkat bulat negatif dan pangkat nol. Yuk simak penjelasan setiap kelompoknya di bawah ini!

PANGKAT BILANGAN BULAT POSITIF

Secara matematis, bilangan berpangkat bilangan bulat positif dapat didefinisikan sebagai berikut:

PANGKAT BILANGAN BULAT NEGATIF DAN NOL

Secara umum, bilangan berpangkat bilangan bulat negatif dapat didefinisikan sebagai berikut:

Sedangkan bilangan dengan pangkat 0 dapat ditentukan:

Catatan:

Jika a=0, maka pangkat 0 tidak memiliki arti, karena:

Eksponen Bilangan Pecahan

Bilangan dengan pangkat bilangan pecahan seringkali dikaitkan dengan bentuk akar bilangan positif.

Pengubahan bentuk pangkat pecahan ke bentuk akar maupun sebaliknya menggunakan aturan berikut:

Bagaimana Sobat? Mudah sekali, bukan? Lanjut yuk!

Notasi Ilmiah Bentuk Pangkat

Notasi ilmiah sangat bermanfaat untuk menuliskan secara singkat bilangan-bilangan yang sangat besar maupun sangat kecil.

Misalkan, kalian ingin menuliskan jumlah uang Rp 5.000.000,- akan lebih mudah kalau dituliskan menjadi 5×10⁶ bukan?

Notasi ilmiah atau yang bisa disebut juga dengan bentuk baku dari suatu bilangan dapat dituliskan secara singkat dalam bentuk:

Catatan:

10^-n berarti terdapat n angka di belakang koma, misal 10^-3 = 0,001.

Sifat-Sifat Bilangan Berpangkat

Ketika melakukan operasi aljabar pada bilangan berpangkat bilangan bulat, kita dapat menggunakan sifat-sifat berikut:

Pssttt.. Kalian wajib hafal semua sifatnya ya! Kalau kalian hafal akan sangat mudah mengerjakan soal eksponennya, lho!

Persamaan Bentuk Eksponen

Tau nggak sih Sobat?

Persamaan Eksponen yaitu persamaan yang melibatkan bentuk eksponen seperti sifat-sifat eksponen dan bentuk akar yang
dihubungkan dengan tanda sama dengan sobat.

Persamaan bentuk eksponen secara sederhana, yaitu:

Untuk macam-macam persamaan eksponen bisa disimak di bawah ini ya!

Gambar di atas jangan lupa di catat di buku catatan kalian ya, Sobat pintar!

Pertidaksamaan Bentuk Eksponen

Biasanya kalau ada persamaan, ada juga pertidaksamaan kan Sobat?

Nah, sekarang yang akan kita bahas disini yaitu Pertidaksamaan Eksponen

Perlu kalian ingat bahwa apapun jenis pertidaksamaannya (termasuk pertidaksamaan eksponen), penyelesaiannya langkah-langkahnya sama antara lain :

Menentukan akar-akarnya
Menentukan garis bilangan dan tandanya
Arsir daerah yang diminta
Tentukan Himpunan Penyelesaiannya.

Persamaan bentuk eksponen secara sederhana, yaitu:

Nah! Itu semua materi dari Fungsi Eksponen, Sobat Pintar.

Sekarang kita tes pemahamanmu di latihan fungsi eksponen, yuk!

Latihan 1

Jawablah soal berikut!

A. 25/2

B. 125/2

C. 25/4

D. 125/4

E. 100

Latihan 2

Jawablah soal berikut!

Sebuah bakteri memiliki ukuran 0,000000015 mm. Bentuk baku dari ukuran bakteri tersebut adalah ....

A. 0,15 x 10^-9

B. 1,5 x 10^-8

C. 15 x 10^-7

D. 15 x 10⁹

E. 1,5 x 10⁸

Latihan 3

Jawablah soal berikut!

A. 243/64

B. 243/8

C. 243/4

D. 9/8

E. 9/4

Latihan 4

Jawablah soal berikut!

A. x = 4

B. x = 3

C. x = 2

D. x = 1

E. x = 0

Latihan 5

Jawablah soal berikut!

A.

B.

C.

D.

E.

Latihan 6

Kerjakan soal berikut ini dengan benar!

A. 2/9

B. 9/4

C. 5/9

D. 7/9

E. 4/5

Latihan 7

Kerjakan soal berikut ini dengan tepat!

A.

B.

C.

D.

E.

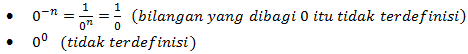
Konsep Logaritma

Sobat udah pada tau dong, kalau gempa itu adalah gelombang atau getaran yang merambat dan aktivitasnya bisa direkam pakai seismograf?

Tapi, kamu tau nggak sih gimana caranya seseorang menentukan intensitas gempa?

Jadi, intensitas gempa itu bisa diukur dengan skala ritcher. Skala ini menggunakan prinsip dari logaritma dengan basis 10.

Nah, pas banget nih kan, setelah membahas mengenai berbagai macam bentuk eksponen, kita akan belajar tentang kebalikan dari eksponen (perpangkatan), yaitu logaritma.

Kenapa bisa disebut kebalikannya?

Karena kalau eksponen kita harus mencari hasil dari bilangan yang dipangkatkan, sedangkan pada logaritma kita harus mencari besar pangkatnya.

Yuk kita pelajari bersama materi logaritma!

Logaritma merupakan suatu operasi yang berkebalikan dengan eksponen (perpangkatan). Logaritma dapat didefinisikan sebagai berikut:

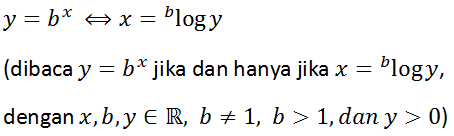
Catatan:

b disebut bilangan pokok
Jika bilangan pokoknya bernilai 10, biasanya tidak ditulis, misal ¹⁰log y = log y
Jika bilangan pokoknya e (bilangan euler, e = 2,718281828...), maka bentuk logaritmanya ditulis dengan ln (dibaca: lon, merupakan logaritma natural), misal ^elog y = ln y

Sifat-Sifat Logaritma

Oleh karena bentuk logaritma masih berhubungan dengan pangkat, maka sifat-sifat logaritma dapat diturunkan dari sifat bilangan berpangkat, yaitu:

PERKALIAN LOGARITMA

PEMBAGIAN LOGARITMA

LOGARITMA DENGAN PANGKAT

Sifat perpangkatan logaritma dapat diturunkan menjadi beberapa sifat berikut:

MENGUBAH BASIS LOGARITMA

Berdasarkan sifat di atas, dapat diturunkan sifat berikut:

PERPANGKATAN LOGARITMA

Persamaan Logaritma

Sebelum ke pembahasan persamaan logaritma, make sure sobat harus sudah paham konsep awal logaritma ya!

Yuk langsung aja kita mulai pembahasan persamaan logaritma!

Persamaan logaritma yaitu persamaan yang memuat bentuk logaritma dengan basis atau numerus, atau keduanya memuat variabel. Bentuknya sama seperti bentuk umum logaritma, tapi pada persamaan logaritma, bentuk logaritmanya ada dua di ruas kiri dan kanan lalu dihubungkan menggunakan tanda sama dengan.

Nggak jauh beda dari materi eksponen, persamaan logaritma juga punya beberapa bentuk yang bikin Sobat pintar lebih gampang untuk mengidentifikasi nilai peubahnya.

Nah, ini nih sobat bentuk-bentuk persamaan logaritma

Gambar di atas ini bisa kalian tulis di buku catatan ya! Yuk lanjut materi selanjutnya

Pertidaksamaan Logaritma

Seperti biasa ya, Sobat, kalau ada persamaan pasti ada pertidaksamaan. Nah, sekarang akan kita bahas pertidaksamaan logaritma

Jangan lupa untuk paham dan hafal tentang sifat-sifat logaritma ya!

Secara khusus, pertidaksamaan logaritma memiliki sifat tersendiri dengan adanya syarat tertentu yang memenuhi. Sifat pertidaksamaan logaritma antara lain:

Nah! Itu semua materi dari pertidaksamaan logaritma Sobat Pintar!