Materi Matematika Minat - Vektor Kelas 11 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
Sebelum kamu belajar mengenai vektor, simak peta belajar bersama berikut ini dulu, ya!
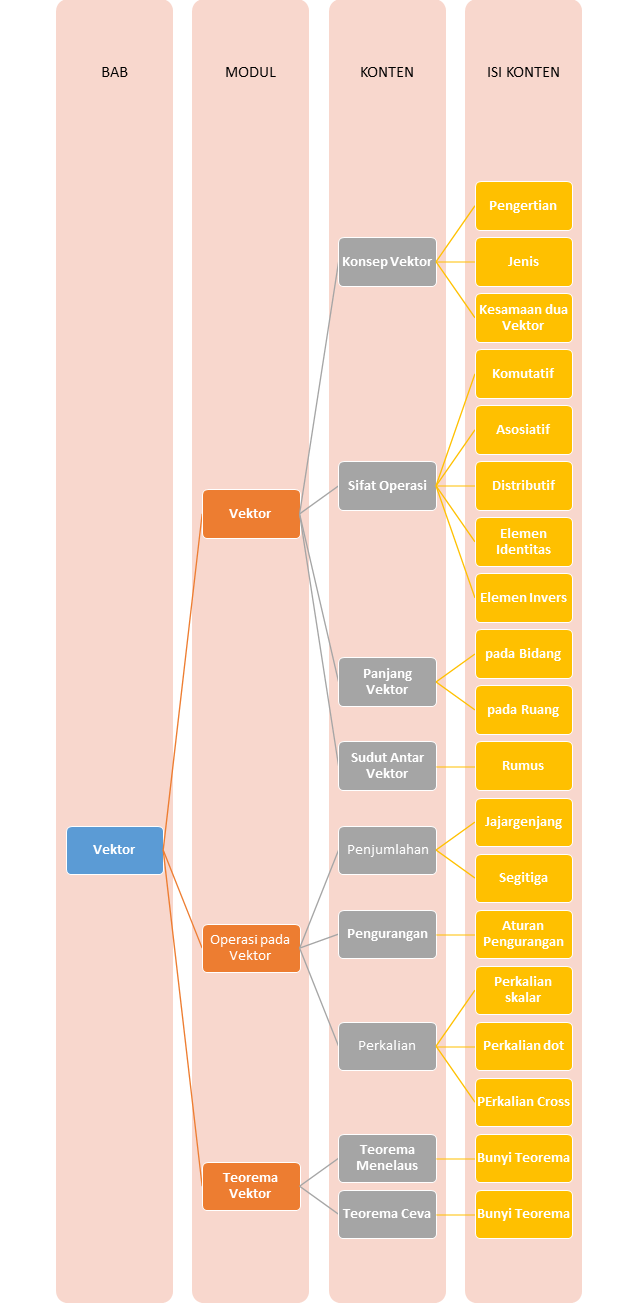
Konsep Vektor

Sebagai anak muda jaman sekarang, Sobat Pintar pasti familiar dengan gambar di atas, bukan?
Betul sekali! GPS pasti sering kita gunakan untuk mencari alamat rumah ya, Sobat.
Tahukah kalian bahwa GPS merupakan salah satu aplikasi dari materi matematika?
Yap! GPS memanfaatkan konsep vektor dalam menentukan sebuah lokasi.

Selain itu, vektor juga pernah kalian pelajari dalam materi fisika, bukan?
Nah! Vektor sendiri merupakan salah satu besaran yang ada di fisika selain besaran skalar.
Jika besaran skalar hanya memiliki nilai saja, vektor merupakan besaran yang memiliki nilai dan arah. Contoh dari besaran skalar adalah panjang, luas, volume, suhu, dll. Sedangkan contoh dari vektor yaitu kecepatan, percepatan, medan magnetik, dan lain sebagainya.
Vektor adalah ruas garis berarah yang memiliki besaran (nilai) dan arah tertentu. Secara geometris, suatu vektor dapat digambarkan sebagai ruas garis berarah dengan panjang ruas garis menyatakan besar vektor dan arah ruas garis menyatakan arah vektor.
Perhatikan contoh vektor berikut:

Seperti pada contoh vektor di atas, sebuah vektor dapat dinotasikan dengan beberapa ketentuan, diantaranya:

JENIS - JENIS VEKTOR
- Vektor nol : vektor yang besarnya nol satuan dan arahnya tak tentu
- Vektor posisi : posisi sebuah titik terhadap titik acuan tertentu yang dinyatakan dengan vektor posisi
- Vektor Basis : vektor yang panjangnya satu satuan dan arahnya searah sumbu koordinat
- Vektor Satuan : suatu vektor yang panjangnya satu satuan.
Secara aljabar, vektor dapat dinyatakan menjadi beberapa cara, yaitu :
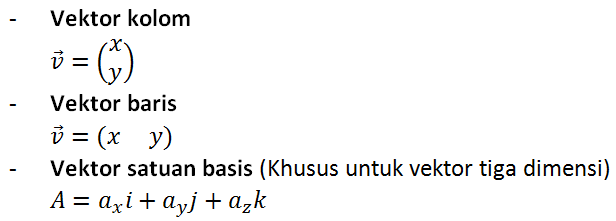
Keterangan:
- Komponen x pada cektor kolom dan baris akan bernilai positif jika arah vektor ke kanan serta bernilai negatif jika arah vektor ke kiri. Sedangkan komponen y akan bernilai positif jika arah vektor ke atas dan bernilai negatif jika arah vektor ke bawah.
- Pada vektor basis, i : vektor satuan yang searah sumbu-x (absis), j : vektor satuan yang searah sumbu-y (ordinat), dan k : vektor satuan yang searah sumbu-z (aplikat). Sedangkan ax : komponen arah sumbu-x, ay : komponen arah sumbu-y, dan az : komponen arah sumbu z.
KESAMAAN DUA VEKTOR
Dua vektor dikatakan sama apabila memiliki panjang dan arah vektornya sama.
Misalkan diketahui vektor v dan u sebagai berikut:
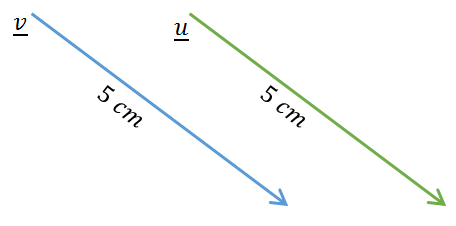
Maka dapat disimpulkan bahwa u = v
Jika diketahui m merupakan vektor dari A ke B, sedangkan n merupakan vektor dari B ke A, maka:
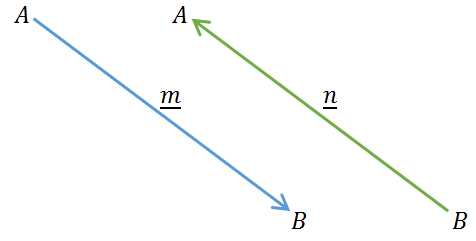
Dapat disimpulkan bahwa m tidak sama dengan n.
Penjumlahan Vektor

Kita dapat mengoperasikan vektor lho, Sobat!
Namun, operasi yang berlaku pada vektor hanya penjumlahan, pengurangan serta perkalian dengan bilangan skalar saja, Sobat.

Dalam penjumlahan dua vektor, terdapat 2 macam cara penjumlahan yang bisa sobat pintar gunakan, yaitu:
Cara Jajar Genjang
Perhatikan gambar berikut!
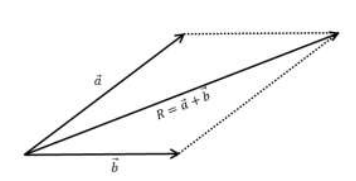
Cara Segitiga
Perhatikan gambar berikut ini!
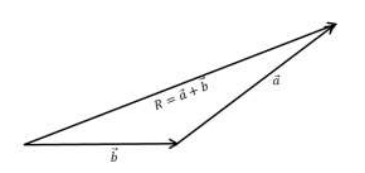
Dalam menghitung penjumlahan vektor jika diketahui koordinatnya, maka :
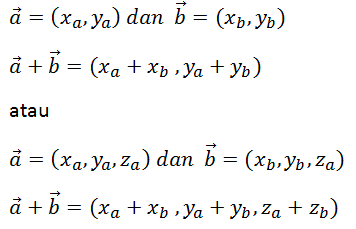
Jika diketahui panjang vektornya dan sudut yang terbentuk adalah ß, maka dapat digunakan rumus berikut:
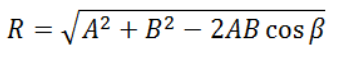
Materi Matematika Minat SMA - 11 Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








