Materi Matematika Minat - Persamaan Trigonometri Kelas 11 MIA

APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Peta Belajar Bersama

Sebelum Sobat Pintar Belajar Mengenai Persamaan Trigonometri, ada baiknya sobat pintar lihat dulu peta konsep berikut agar sobat pintar tahu apa saja yang akan dipelajari.

Materi Prasyarat

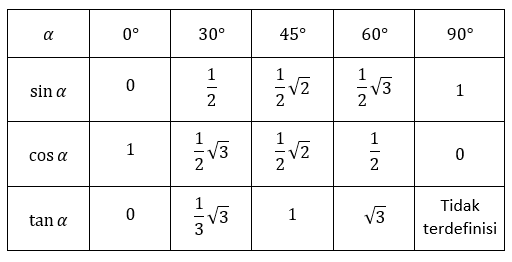
Sobat pintar tidak perlu khawatir jika lupa dengan nilai perbandingan trigonometri pada sudut istimewa, karena kakak sudah siapkan tabel nilainya sebagai berikut.

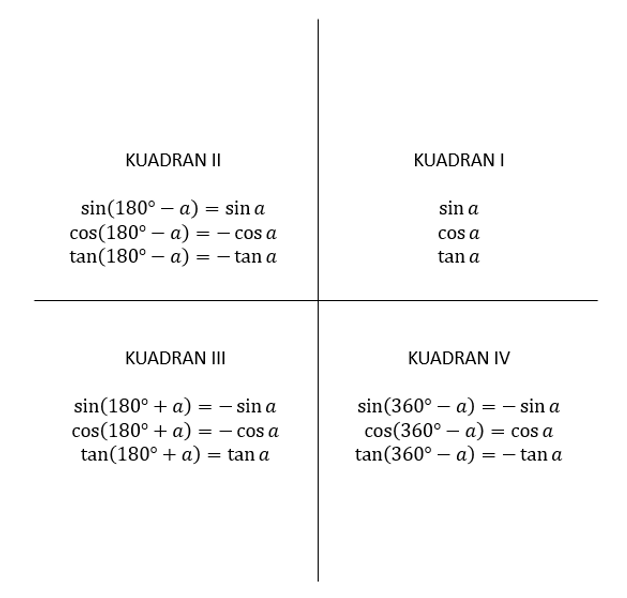
Selain nilai perbandingan trigonometri di atas, sobat pintar juga harus ingat perbandingan trigonometri di berbagai kuadran. Sekali lagi, sobat pintar tidak perlu risau karena kakak sudah siapkan.

Persamaan Trigonometri Dasar

Sobat Pintar pasti sudah mengetahui tentang trigonometri, bukan?

Nah kali ini kita akan belajar tentang PERSAMAAN TRIGONOMETRI.

Perbedaan antara persamaan trigonometri dengan persamaan yang lain adalah persamaan trigonometri mengandung fungsi trigonometri dari suatu sudut yang belum diketahui nilainya.

Dalam menyelesaikan persamaan trigonometri bervariabel x, kita akan mencari nilai dari sudut x sehingga persamaan tersebut bernilai benar untuk suatu daerah tertentu, biasanya daerahnya dibatasi untuk satu putaran

Tidak perlu lama-lama, bentuk persamaan trigonometri dasar ada 3, yaitu:

PERSAMAAN SINUS

Secara umum, bentuk persamaan trigonometri fungsi sinus, yaitu:

Dalam bentuk radian (pi) persamaan fungsi sinus adalah sebagai berikut.

PERSAMAAN COSINUS

Sedangkan, bentuk umum persamaan trigonometri fungsi cosinus adalah:

Dalam bentuk radian (pi) persamaan fungsi cosinus adalah sebagai berikut.

PERSAMAAN TANGEN

Terakhir, bentuk umum persamaan trigonometri fungsi tangen adalah:

Dalam bentuk radian (pi) persamaan fungsi tangen adalah sebagai berikut.

Sebagian sobat pintar mungkin ada yang bingung dengan maksud dari rumus-rumus persamaan trigonometri tadi, untuk memperjelas, sobat pintar bisa perhatikan contoh soal berikut.

Tentukan himpunan penyelesaian dari persamaan trigonometri berikut!

Pembahasan:

Persamaan Trigonometri Bentuk Lain

Persamaan trigonometri tidak selamanya akan berbentuk seperti bentuk umum yang telah sobat pintar pelajari. Untuk itu sobat pintar perlu rumus bantuan untuk bisa menyelesaikan persamaan tersebut.

Misal sobat pintar bertemu dengan persamaan m cos x + n sin x = c, maka sobat pintar bisa menggunakan rumus berikut untuk mengubahnya menjadi seperti bentuk umum, berikut rumusnya

Selain bentuk barusan, terdapat juga bentuk persamaan kuadrat trigonometri yang dapat diselesaikan dengan memfaktorkan persamaan tersebut untuk mencari penyelesaiannya. Misal persamaan kuadrat trigonometri yang mengandung sin x seperti berikut.

Latihan 1

Jawablah soal berikut!

A. {30°, 90°, 180°, 360°}

B. {45°, 90°, 180°, 270°}

C. {45°, 90°, 225°, 270°}

D. {30°, 45°, 60°, 90°}

E. {30°, 180°, 225°, 270°}

Latihan 2

Jawablah soal berikut!

A. {30°, 110°, 150°, 230°, 270°}

B. {10°, 30°, 110°, 150°, 230°, 270°}

C. {10°, 30°, 150°, 225°, 270°}

D. {30°, 120°, 160°, 200°, 240°}

E. {30°, 60°, 90°, 180°, 270°}

Latihan 3

Jawablah soal berikut!

A. 0°

B. 10°

C. 15°

D. 30°

E. 45°

Latihan 4

Jawablah soal berikut!

A.

B.

C.

D.

E.

Latihan 5

Jawablah soal berikut!

A.

B.

C.

D.

E.

Latihan 6

Kerjakan soal berikut dengan tepat!

A.

B.

C.

D.

E.

Latihan 7

Kerjakan soal berikut dengan tepat!

A. {50°, 307°}

B. {106°, 254°}

C. {113°, 353°}

D. {148°, 219°}

E. {166°, 201°}

Rumus Jumlah dan Selisih Dua Sudut

Sobat Pintar pasti sudah mengetahui nilai-nilai sudut istimewa. Bagaimana kita bisa menentukan nilai sudut yang tidak termasuk dalam sudut istimewa?

Tenang saja, Sobat! Nilai suatu sudut yang bukan merupakan sudut istimewa dapat kita tentukan dengan menggunakan jumlah dan selisih dua sudut sinus, cosinus, dan tangen, lho!

Yuk langsung kita pelajari bersama!

RUMUS SINUS JUMLAH DAN SELISIH DUA SUDUT

RUMUS COSINUS JUMLAH DAN SELISIH DUA SUDUT

Sobat pintar ingin tahu darimana rumus di atas ini berasal?

Rumus ini berasal dari rumus sebelumnya, yaitu rumus jumlah dan selisih dua sudut sinus, berikut caranya

RUMUS TANGEN JUMLAH DAN SELISIH DUA SUDUT

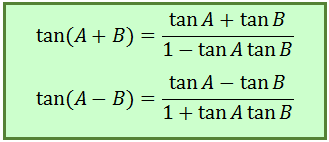
Rumus tangen di atas didapatkan dengan menggunakan rumus jumlah dan selisih dua sudut sinus dan cosinus. Bagaimana bisa?

Rumus Sudut Rangkap

Rumus trigonometri untuk sudut rangkap dapat dicari dengan memanfaatkan rumus jumlah dan selisih dua sudut pada pembahasan sebelumnya.

RUMUS SINUS SUDUT RANGKAP

RUMUS COSINUS SUDUT RANGKAP

RUMUS TANGEN SUDUT RANGKAP

Rumus Setengah Sudut

Sebelumnya ada rumus sudut rangkap alias dua kali lipat, kenapa tidak dibahas juga rumus setengah sudut, lawannya dari sudut rangkap. Berikut rumus-rumusnya yaa sobat

RUMUS SINUS SETENGAH SUDUT

RUMUS COSINUS SETENGAH SUDUT

RUMUS TANGEN SETENGAH SUDUT

Rumus Perkalian, Penjumlahan, dan Pengurangan

RUMUS PERKALIAN SINUS DAN COSINUS

Bagaimana jadinya yaa kalau sinus dan cosinus dikalikan satu sama lain? Apakah ada rumusnya untuk mempermudah kita menyelesaikan soal?

Jawabannya adalah ada, sobat pintar hanya tinggal lihat rumus di bawah ini

Sekarang, apakah sobat pintar penasaran tentang dari mana sih rumus ini berasal? Rumus ini berasal dengan mengeliminasi rumus-rumus yang ada sebelumnya loh sobat, simak penjelasan berikut yaa

Kita eliminasi rumus jumlah dan selisih sinus, dan akan diperoleh

Tadi eliminasi dengan penjumlahan, sekarang eliminasi dengan pengurangan, dan didapatkan

Selanjutnya, untuk mendapatkan rumus perkalian sinus dan cosinus, kita eliminasi rumus jumlah dan selisih cosinus.

Kita ulang lagi tetapi eliminasi kali ini dengan dikurang

RUMUS PENJUMLAHAN DAN PENGURANGAN SINUS DAN COSINUS

Sepanjang pembelajaran kali ini kita merubah dari rumus yang satu, ke rumus lain yang merupakan rumus baru, dan kali ini yang akan kita lakukan masih sama, yaitu mencari rumus pernjumlahan dan pengurangan sinus dan cosinus. Untuk mencari rumus ini, kita akan menggunakan rumus perkalian sinus dan cosinus dengan cara berikut.