Materi Matematika Minat - Polinomial Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
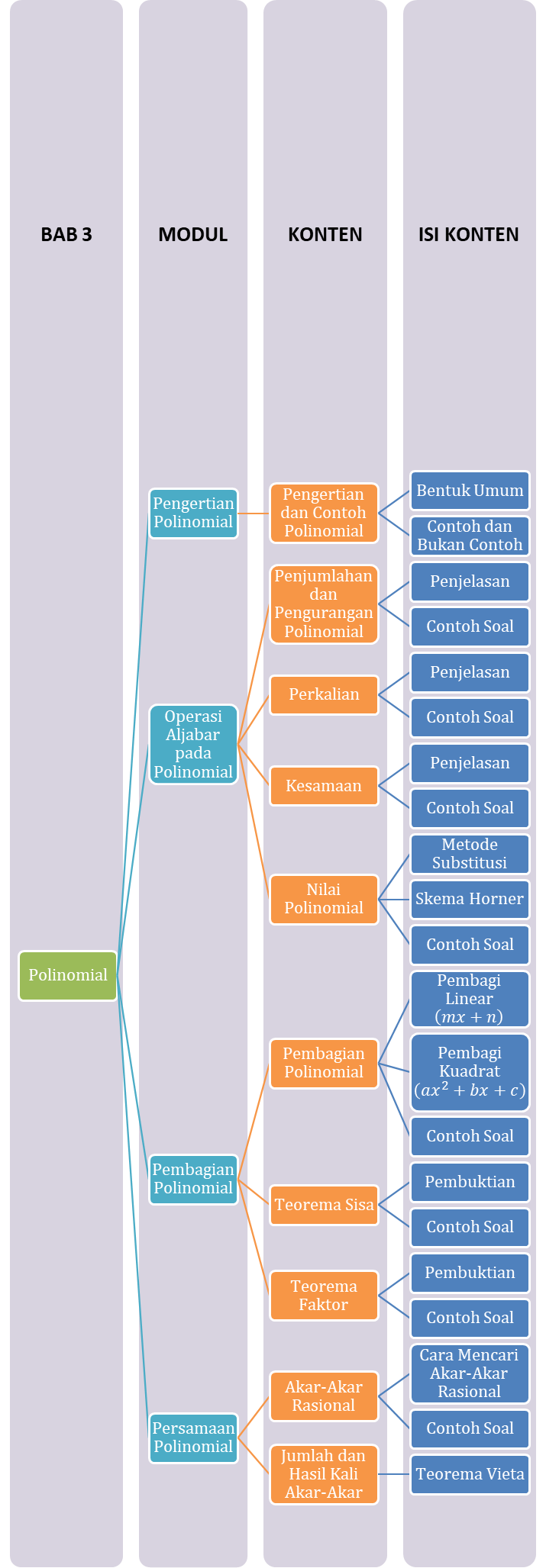
Sebelum sobat pintar mempelajari tentang materi Polinomial, sobat bisa perhatikan Peta Belajar Bersama ini dulu ya!
Pengertian dan Contoh Polinomial


Suatu produk berbentuk kubus akan dikemas dan membutuhkan perlindungan bubble wrap setebal 8 cm untuk atas dan bawah serta 4 cm untuk samping-sampingnya. Berapakah volume kemasan produk tersebut?
Persoalan seperti ini merupakan masalah yang berkaitan dengan polinomial, bagaimana kaitannya? Simak sampai akhir yaa....
Pertama-tama sobat pintar harus tau, apa itu polinomial?
Polinomial atau suku banyak adalah suatu bentuk aljabar yang terdiri atas beberapa suku dan memuat satu variabel berpangkat bulat positif.
Secara umum polinomial dalam x dan berderajat n dapat dituliskan sebagai berikut.

Agar sobat pintar lebih paham berikut adalah contoh dan bukan contoh dari polinomial

Penjumlahan dan Pengurangan Polinomial


Operasi aljabar seperti penjumlahan dan pengurangan ternyata bisa lho dilakukan pada polinomial. Untuk menjumlah atau mengurang pada polinomial sobat pintar hanya perlu menjumlahkan atau mengurangkan antar koefisien suku-suku sejenis
Apasih yang dimaksud suku sejenis? Apakah x3 dan 3x suku-suku yang sejenis?
Suku-suku sejenis adalah suku-suku yang memiliki variabel berpangkat sama, jadi x3 dan 3x itu tidak sejenis yaa sobat. Contoh suku-suku sejenis adalah x4 dan 2x4 dimana kedua suku sama-sama memiliki variabel berpangkat 4.
Agar sobat pintar lebih paham kita coba ke contoh soal saja yaa.
Diketahui polinomial:
p(x) = 6x4 -8x2 +7x +10
q(x) = 10x2 +11x -12
Berapakah hasil penjumlahan dan pengurangan polinomial p(x) dan q(x)?
Pembahasan:
Penjumlahan polinomial p(x) dan q(x)
p(x) + q(x) = (6x4 -8x2 +7x +10) + (10x2 +11x -12)
p(x) + q(x) = 6x4 +(-8x2 +10x2) +(7x +11x) +(10 -12)
p(x) + q(x) = 6x4 +(-8 +10)x2 +(7 +11)x +(-2)
p(x) + q(x) = 6x4 +2x2 +18x -2
Pengurangan polinomial p(x) dan q(x)
p(x) - q(x) = (6x4 -8x2 +7x +10) - (10x2 +11x -12)
p(x) - q(x) = 6x4 -8x2 +7x +10 -10x2 -11x +12
p(x) - q(x) = 6x4 +(-8x2 -10x2) +(7x -11x) +(10 +12)
p(x) - q(x) = 6x4 +(-8-10)x2 +(7-11)x +22
p(x) - q(x) = 6x4 -18x2 -4x +22
Pembagian Polinomial


Sobat pintar pasti sudah biasa untuk membagi bilangan dengan cara diatas, nah sekarang bagimana yaa kalau pembagiannya bukan sekedar bilangan, melainkan polinomial.
Ada dua cara untuk menyelesaikan pembagian polinomial sobat, pertama dengan cara diatas atau biasa disebut cara bersusun dan yang kedua dengan cara horner.
Sebelum membagi polinomial mari kita ulas kembali pembagian. Pembagian secara umum dapat ditulis:
Bilangan yang dibagi = (pembagi × hasil bagi) + sisa
Pada polinomial juga berlaku hal yang sama, misal polinomial f(x) dibagi oleh p(x) menghasilkan h(x) dan sisanya s(x), maka dapat ditulis:
f(x)=p(x)·h(x) +s(x)
Pembagian polinomial oleh bentuk linear (mx+n)
Misal polinomial f(x) dibagi (mx+n) maka dapat ditulis

Agar sobat pintar tidak bingung dengan penjelasan barusan, sobat pintar perhatikan contoh soal berikut.
Tentukan hasil bagi dan sisa pembagian dari (3x4 –5x3 +7x2 +5x +2) : (3x+1)
Cara bersusun

Cara Horner

Pembagian polinomial oleh bentuk kuadrat (ax2+bx+c) dengan a bukan nol
Pada pembagian ini cara horner hanya bisa dipakai jika pembaginya bisa difaktorkan. Misal polinomial f(x) dibagi (ax2+bx+c) dengan a bukan 0, maka langkah penyelesaian cara horner adalah

Untuk mempermudah sobat pintar dalam memahami penjelasan diatas sobat pintar bisa menyimak contoh soal berikut.
Tentukan hasil bagi dan sisa pembagian dari polinomial f(x)=x4 –3x2 +2x –1 oleh x2 –x –2
Cara bersusun

Cara Horner
Pembagi x2 –x –2 difaktorkan menjadi (x–2)(x+1), artinya k1=2, k2=–1, dan a=1

Akar-Akar Rasional


Sepanjang pembahasan polinomial kita selalu menuliskan polinomial dalam bentuk f(x), kali ini kita akan menuliskannya dalam bentuk persamaan, tahukah sobat pintar bagaimana bentuk dari persamaan polinomial?
Bentuk umum persamaan polinomial dengan variabel x dapat dituliskan sebagai berikut.
anxn+a(n–1)x(n–1)+a(n–2)x(n–2)+ ... +a2x2+a1x+a0=0
Dengan an tidak 0 dan n bilangan asli
Sama halnya seperti persamaan kuadrat, persamaan polinomial juga memiliki akar-akar persamaan rasional. Untuk persamaan polinomial berderajat dua akar–akar persamaannya bisa dicari dengan cara yang sama dengan mencari akar-akar persamaan kuadrat. Namun, untuk mencari akar-akar rasional dari persamaan polinomial berderajat lebih dari dua harus melewati langkah-langkah berikut:
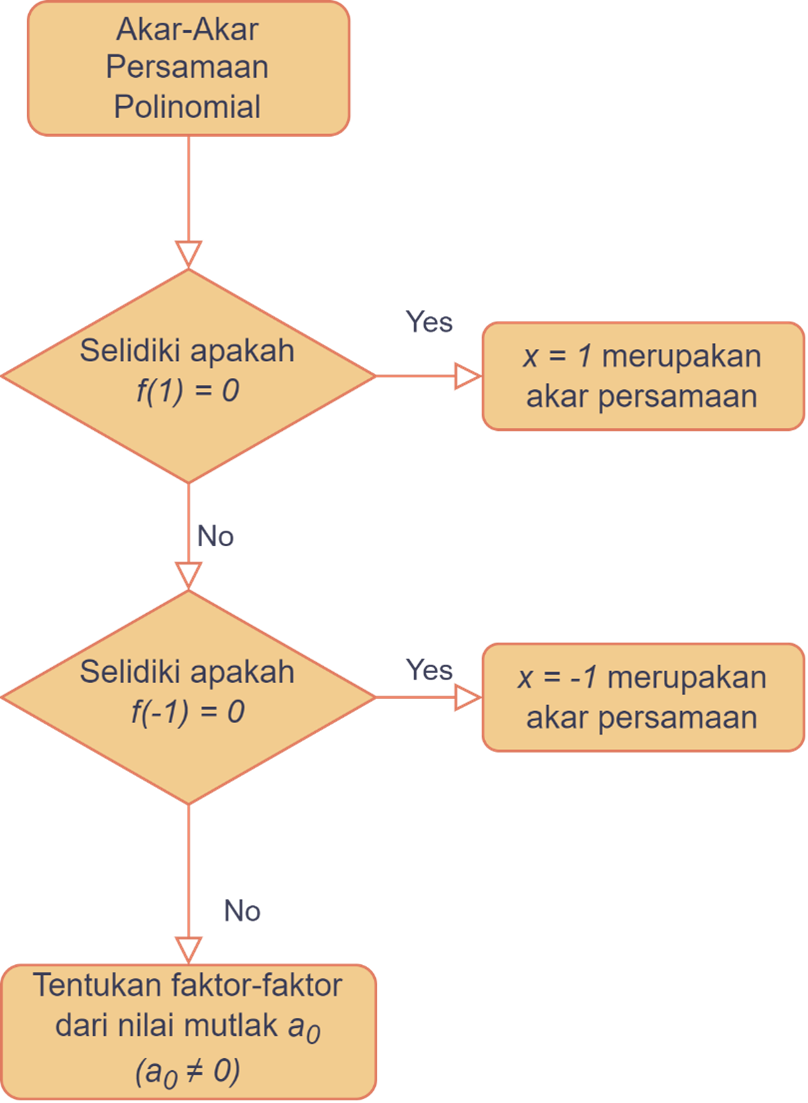
Untuk memahami diagram diatas sebaiknya kita langsung mencoba ke contoh soal
Temukan seluruh akar-akar rasional dari persamaan polinomial x4–15x2–10x+24=0
Langkah 1: Selidiki f(1)=14–15(1)3–10(1)+24=1–15–10+24=0, artinya x=1 merupakan akar persamaan,
Untuk mencari akar yang lain, kita bisa gunakan cara horner berikut untuk mendapatkan hasil bagi
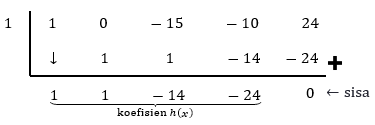
Hasil bagi pembagian diatas adalah h(x)=x3+x2–14x–24
Langkah 1 pada hasil bagi h(x): Selidiki h(1)=13+12–14(1)–24=1+1–14–24=–36, artinya x=1 bukan merupakan akar persamaan
Langkah 2 pada hasil bagi h(x): Selidiki h(–1)=(–1)3+(–1)2–14(–1)–24=–1+1+14–24=–10, artinya x=–1 bukan merupakan akar persamaan
Langkah 3 pada hasil bagi h(x): nilai mutlak a0=|a0|=|–24|=24. Faktor dari 24 adalah ±1,±2,±3,±4,±6,±8,±12, dan ±24. Karena x=±1 bukan merupakan akar, maka x=±1 tidak perlu dicoba lagi
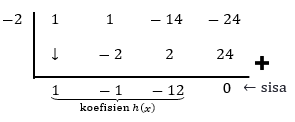
Karena sisa =0 maka x=–2 merupakan akar dari h(x)=0 dengan hasil bagi x2–x–12,
Untuk mencari akar yang lain, kita bisa memfaktorkan x2–x–12=0 sebagai berikut
x2–x–12=0
(x–4)(x+3)=0
x=4 atau x=–3
Jadi, akar–akar rasional dari persamaan x4–15x2–10x+24=0 adalah –3,–2,1, dan 4
Materi Matematika Minat SMA - 11 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








