Materi Matematika - Transformasi Kelas 9 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat!
Sebelum kita belajar tentang Transformasi, coba kalian perhatikan Peta Belajar Bersama ini dulu, ya!
Refleksi

Refleksi atau pencerminan merupakan satu jenis transformasi yang memindahkan setiap titik pada suatu bidang dengan mengggunakan sifat bayangan cermin dari titik-titik yang dipindahkan. Perhatikan gambar di bawah.
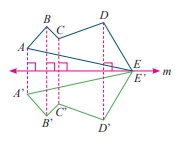
Gambar di atas menunjukkan contoh refleksi (pencerminan) bangun datar ABCDE pada garis m.
Perhatikan bahwa ruas garis yang menghubungkan titik dan bayangannya tegak lurus terhadap garis m. Garis m disebut garis refleksi untuk ABCDE dan bayangannya A’B’C’D’E’. Karena E terletak pada garis refleksi, titik awal dan bayangannya berada di titik yang sama. Jarak antara A terhadap garis m sama dengan jarak A’ terhadap garis m, begitu pula untuk titik sudut yang lainnya dan bayangannya yang memiliki jarak sama terhadap garis refleksi m.
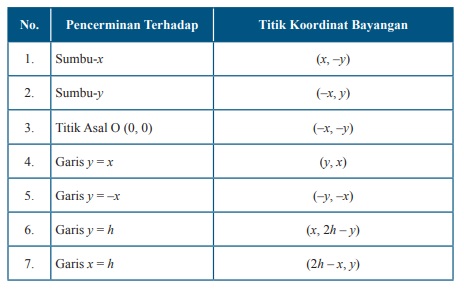
Jika diketahui sebarang titik dengan koordinat (x, y) pada koordinat kartesius, maka koordinat bayangan hasil pencerminannya dapat dilihat pada tabel berikut.
Translasi

Translasi merupakan salah satu jenis transformasi yang bertujuan untuk memindahkan semua titik suatu bangun dengan jarak dan arah yang sama.

Translasi pada bidang Kartesius dapat dilukis jika kamu mengetahui arah dan seberapa jauh gambar bergerak secara mendatar dan atau vertikal. Untuk nilai yang sudah ditentukan a dan b yakni translasi 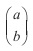 memindahkan setiap titik P (x, y) dari sebuah bangun pada bidang datar ke P' (x + a, y + b). Translasi dapat disimbolkan dengan (x, y) --> (x + a, y + b).
memindahkan setiap titik P (x, y) dari sebuah bangun pada bidang datar ke P' (x + a, y + b). Translasi dapat disimbolkan dengan (x, y) --> (x + a, y + b).
Rotasi

Rotasi merupakan salah satu bentuk transformasi yang memutar setiap titik pada gambar sampai sudut dan arah tertentu terhadap titik yang tetap. Titik tetap ini disebut pusat rotasi. Besarnya sudut dari bayangan benda terhadap posisi awal disebut dengan sudut rotasi.
Untuk rotasi searah jarum jam, sudut diberi tanda negatif (–)
Untuk rotasi berlawanan arah jarum jam, sudut diberi tanda positif (+)
Brikut merupakan rumus praktis dari rotasi dengan pusat rotasi (0,0)
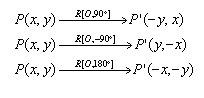
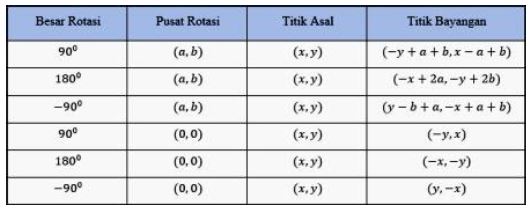
Dilatasi

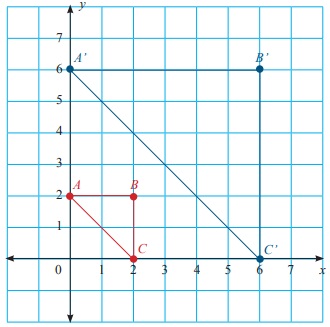
Dilatasi terhadap titik pusat merupakan perkalian dari koordinat tiap-tiap titik pada suatu bangun datar dengan faktor skala sebesar k. Faktor skala menentukan apakah suatu dilatasi merupakan pembesaran atau pengecilan. Secara umum dilatasi dari suatu koordinat (x, y) dengan faktor skala k akan menghasilkan koordinat (kx, ky) atau dapat ditulis (x, y) --> (kx, ky).
Ketika k > 1 maka dilatasi tersebut termasuk ke dalam pembesaran, tetapi jika 0 < k < 1 maka dilatasi tersebut termasuk ke dalam pengecilan. Untuk memperbesar atau memperkecil bangun, letak pusat dilatasi dapat di dalam, di luar, atau pada tepi bangun yang akan didilatasikan.
Kekongruenan Bangun Datar

Kongruen adalah keadaan dimana dua bangun datar memiliki ukuran yang sama dan dikatakan sebangun.
Dari pengertian tersebut dapat diketahui bahwa semua bangun datar yang kongruen sudah pasti sebangun, namun bangun datar yang sebangun belum tentu kongruen.
Jadi, ciri-ciri bangun datar yang kongruen adalah :
– Memiliki panjang sisi yang sama.
– Memiliki bentuk yang sama.
– Memiliki besar sudut yang sama.
– Sebangun
Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu :
(i) sisi-sisi yang bersesuaian sama panjang
(ii) sudut-sudut yang bersesuaian sama besar
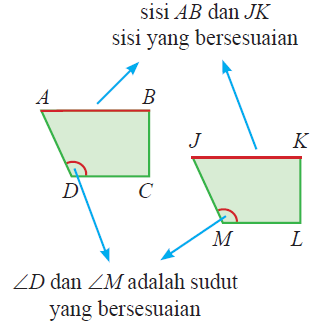
Sudut-sudut yang bersesuaian:
sudut A dan sudut J ---> sudut A = sudut J
sudut B dan sudut K ---> sudut B = sudut K
sudut C dan sudut M ---> sudut D = sudut M
Sisi-sisi yang bersesuaian:
AB dan JK ---> AB = JK
BC dan KL ---> BC = KL
CD dan LM ---> CD = LM
DA dan MJ ---> DA = MJ
Jika bangun ABCD dan JKLM memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ![]()
Jika bangun ABCD dan JKLM tidak memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ![]()
Catatan:
Ketika menyatakan dua bangun sebangun dinyatakan berdasarkan titik-titik sudut yang bersesuaian dan berurutan, contohnya:
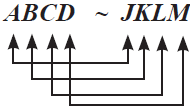 atau
atau 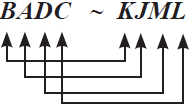 atau
atau 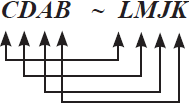
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








