Materi Matematika - Lingkaran Kelas 9 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, Ini nih ada Peta Belajar Bersama Matematika di BAB Ketujuh
Yuk belajar bersama.....
Lingkaran dan Unsur-unsurnya

Apasih yang dimaksud dengan lingkaran? Yuk, Sobat Pintar perhatikan penjelasan dibawah ini.
Lingkaran merupakan kumpulan titik-titik pada garis bidang datar yang semuanya berjarak sama dari titik tertentu. Titik ini disebut pusat lingkaran. Kumpulan titik-titik tersebut jika dihubungkan membentuk suatu garis lengkung.
Keliling dan Luas Lingkaran

Nah, Sobat Pintar. Tadi kita sudah selesai membahas pengertian lingkaran, sekarang waktunya mengetahui lebih lanjut tentang unsur-unsur lingkaran.
Unsur-unsur Lingkaran:
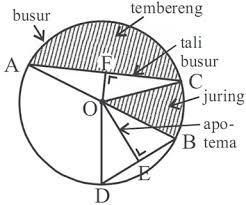
- Titik Pusat
Titik pusat lingkaran adalah titik yang terletak di tengah-tengah lingkaran. Titik O merupakan titik pusat lingkaran. - Jari-Jari (r)
Jari-jari lingkaran adalah garis dari titik pusat lingkaran ke lengkungan lingkaran. Garis AO, garis OB, dan OD merupakan jari-jari lingkaran. - Diameter (d)
Diameter adalah garis lurus yang menghubungkan dua titik pada lengkungan lingkaran dan melalui titik pusat. Garis AB merupakan diameter lingkaran. - Busur
Dalam lingkaran, busur lingkaran merupakan garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik sebarang di lengkungan tersebut. - Tali Busur
Tali busur lingkaran adalah garis lurus dalam lingkaran yang menghubungkan dua titik pada lengkungan lingkaran. Berbeda dengan diameter, tali busur tidak melalui titik pusat. - Tembereng
Tembereng adalah luas daerah dalam lingkaran yang dibatasi oleh busur dan tali busur. - Juring
Juring lingkaran adalah luas daerah dalam lingkaran yang dibatasi oleh dua buah jari-jari lingkaran dan sebuah busur yang diapit oleh kedua jari-jari lingkaran tersebut. - Apotema
Pada sebuah lingkaran, apotema merupakan garis yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran tersebut. Garis yang dibentuk bersifat tegak lurus dengan tali busur.
Garis Singgung Persekutuan Luar Dua Lingkaran

Perhatikan gambar di bawah ini!
Lingkaran A berpusat di A dengan jari-jari AD = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2.
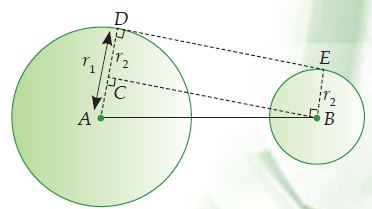
AB adalah jarak kedua titik pusat lingkaran (s). DE adalah garis singgung persekutuan luar dua lingkaran, dimana DE tegak lurus dengan AD. Melalui titik B, dapat ditarik garis BC yang sejajar garis DE (BC//DE), sehingga BE = CD = r2, dan sudut ACB = 90o.
Maka segitiga ACB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras,
AB2 = AC2 + BC2
BC2 = AB2 – AC2
= AB2 – (AD – CD)2
= s2 – (r1 – r2)2
Karena BC//DE dan sudut ACB = sudut ADE = 90o, maka DE = BC. Jadi, DE2 = s2 – (r1 – r2)2. Maka panjang garis singgung persekutuan luar dua lingkaran dirumuskan:
l2 = s2 – (r1 – r2)2
dengan r1 > r2, dan
l : panjang garis singgung persekutuan luar dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1: jari-jari lingkaran pertama
r2: jari-jari lingkaran kedua
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








