Materi Matematika Wajib - Fungsi Kelas 11 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
Sebelum kita belajar tentang Fungsi, coba kita perhatikan peta belajar bersama di bawah ini!
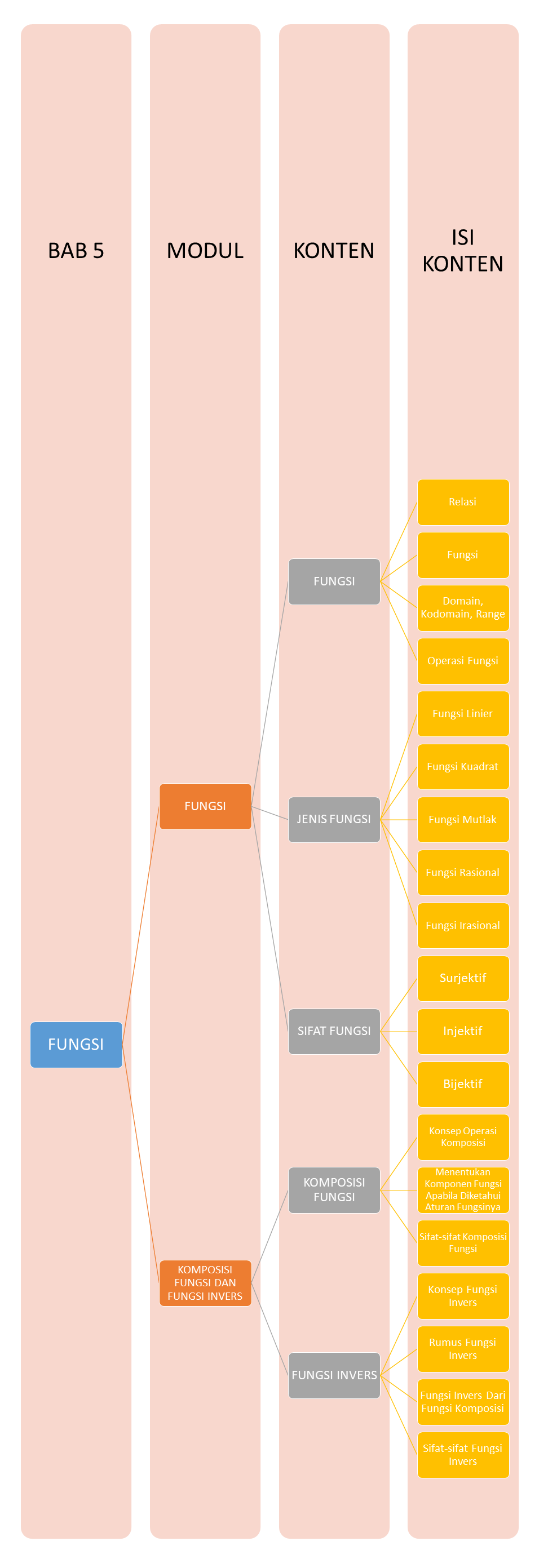
Yuk belajar bersama!
Fungsi

Sumber: Pngdownload.id
Sobat Pintar pasti pernah mengetahui cara kerja suatu mesin, bukan?
Jika bahan baku dimasukkan ke dalam mesin maka mesin akan memprosesnya dan menghasilkan suatu produk baru. Nah! Dalam materi matematika juga ada loh yang konsepnya sama dengan mesin.
Yap! Fungsi.
Fungsi memiliki konsep seperti mesin lho, sobat! Jadi daerah asal fungsi sebagai bahan bakunya dan daerah hasil sebagai produknya.
Kita pelajari lebih lanjut materi fungsi yuk!
RELASI
Sobat pintar masih ingat tidak apa itu relasi?
Relasi menyatakan hubungan antara anggota himpunan dengan anggota himpunan lain. Himpunan A dan Himpunan B dikatakan memiliki relasi jika terdapat anggota himpunan yang saling berpasangan dengan hubungan tertentu
Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu:
a) Diagram Panah
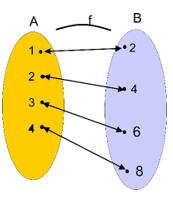
b) Himpunan Pasangan Berurutan
K = {(1,2),(2,4),(3,6),(4,8),(5,10)
c) Diagram Kartesius
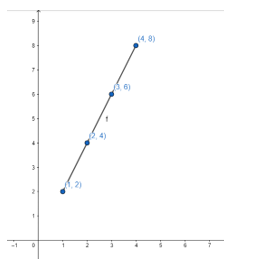
FUNGSI
Fungsi (pemetaan) adalah relasi dari himpunan A ke himpunan B, jika terdapat setiap anggota berpasangan tepat satu anggota himpunan B. Semua anggota himpunan A disebut domain (daerah asal), semua anggota himpunan B disebut kodomain (daerah kawan) dan hasil dari pemetaan himpunan A dan himpunan B adalah daerah hasil (range). Sama seperti relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, diagram kartesius, dan himpunan pasangan berurutan
Suatu fungsi secara sistematis dapat dituliskan:
f:x -> ax+b (fungsi f memetakan x ke ax+b)
atau
f(x) = ax+b (fungsi dalam x)
atau
y= ax+b (y adalah fungsi dari x)
Catatan
Jika f(x)=y, maka y merupakan bayangan x (image), sedangkan x merupakan prabayangan dari y (pra-image)
Fungsi dapat disajikan dalam bentuk:
- diagram panah
- diagram cartesius
- himpunan pasangan berurutan
DOMAIN, KODOMAIN DAN RANGE FUNGSI
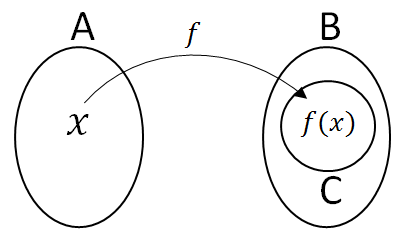
Jika f adalah suatu fungsi dari A ke B, maka himpunan A disebut domain (daerah asal) dan himpunan B disebut kodomain (daerah kawan). Sedangkan himpunan B yang berpasangan (himpunan C) disebut range (hasil) fungsi f.
Aturan yang memasangkan anggota himpunan A dengan anggota-anggota himpunan B disebut aturan fungsi f.
Domain suatu fungsi dapat ditetapkan secara jelas (eksplisit). Jika domain tidak ditetakan dengan jelas, maka digunakan kesepakatan bahwa domainnya merupakan himpunan bilangan real.
Syarat yang harus dipenuhi agar suatu fungsi terdefinisi (memiliki daerah hasil di himpunan bilangan real), yaitu:
- fungsi dalam akar
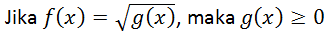
- fungsi pecahan
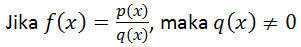
- fungsi pecahan, dimana penyebutnya merupakan fungsi lain dalam bentuk akar
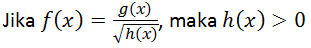
- fungsi logaritma
Jika f(x) = g(x) log h(x), maka h(x)>0, g(x)>0 dan g(x) tidak sama dengan 1
GRAFIK FUNGSI
Suatu fungsi dari himpunan A ke himpunan B dapat dbuat grafik pemetaannya dengan menggunakan diagram cartesius. Grafik suatu fungsi dapat berupa garis lurus maupun kurva.
Langkah-langkah menggambar grafik fungsi pada koordinat cartesius, yaitu:
- Tentukan domain (jika belum diketahui secara pasti, pilih beberapa bilangan bulat disekitar nol)
- Tentukan pasangan berurutan dari fungsi tersebut
- Gambar pasangan berurutan sebagai titik pada koordinat cartesius
- Hubungkan titik-titik yang sudah digambar pada koordinat cartesius
Berdasarkan grafik suatu fungsi, dapat ditentukan domain dan range nya. Domain fungsi terletak pada sumbu x, sedangkan kodomain fungsi terletak pada sumbu y.
OPERASI ALJABAR FUNGSI
Pada dua atau lebih fungsi dapat dilakukan operasi aljabar seperti penjumlahan, pengurangan, perkalian dan pembagian.
Operasi aljabar yang berlaku pada fungsi, antara lain:

Contoh Soal Operasi Fungsi
CONTOH SOAL 1: Penjumlahan Dua Fungsi
Jawablah soal berikut ini!

Pembahasan
(f+g)(x)=f(x)+g(x)
=(x2+2x-3)+(x-1)
=x2+3x-4
Jadi, nilai (f+g)(x) adalah x2+3x-4
CONTOH SOAL 2: Selisih Dua Fungsi
Jawablah soal berikut ini!

Pembahasan
(f-g)(x)=f(x)-g(x)
= (2x-6)-(x-4)
=x-2
Jadi, nilai (f-g)(x) adalah x-2
CONTOH SOAL 3: Perkalian Dua Fungsi
Jawablah soal berikut ini!

Pembahasan
(f×g)(x)=f(x)×g(x)
=(x+5)×(3x-7)
=3x2+8x-35
Jadi, nilai (f×g)(x) adalah 3x2+8x-35
CONTOH SOAL 4: Pembagian Dua Fungsi
Jawablah soal berikut ini!
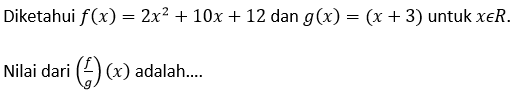
Pembahasan
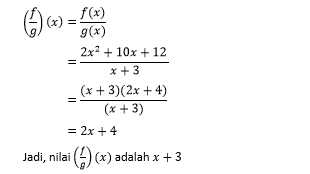
Fungsi Komposisi

KONSEP OPERASI KOMPOSISI
Suatu fungsi dapat digabungkan menjadi fungsi yang baru dengan syarat tertentu yaitu operasi komposisi. Operasi komposisi dilambangkan dengan “o” (komposisi/bundaran).
Fungsi komposisi yang dapat dibentuk dari dua fungsi f(x) dan g(x), yaitu:
- (g o f) artinya fungsi f disubtitusikan pada fungsi g
- (f o g) artinya fungsi g disubtitusikan pada fungsi f
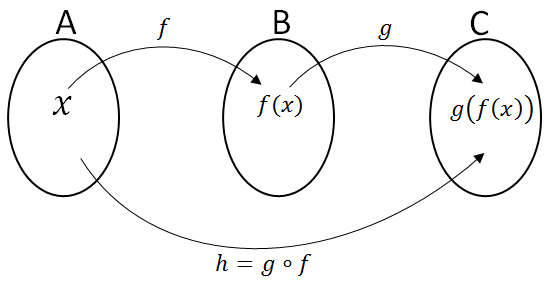
Jika f:A -> B dan g:B -> C, maka h:A -> C atau h: x -> g(f(x))
Jadi, secara sistematis dapat dirumuskan:
h(x) = (g o f)(x) = g(f(x))
Catatan:
Tidak semua fungsi dapat dikomposisikan. Dua fungsi dapat digabungkan apabila memenuhi syarat berikut:
- Jika daerah hasil f merupakan himpunan bagian dari daerah asal g
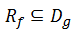
- Jika daerah hasil f dengan daerah asal g diiriskan, hasilnya bukan himpunan kosong
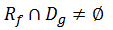
MENENTUKAN KOMPONEN FUNGSI APABILA DIKETAHUI ATURAN FUNGSINYA
Jika menentukan komposisi dari dua fungsi tinggal disubstitusikan, untuk menentukan salah satu fungsi jika diketahui komponen fungsinya dapat menggunakan cara-cara pada contoh berikut:
Jika diketahui f(x) dan g(x) pada R dengan f(x)=x2 – 4. Tentukan rumus fungsi g(x) jika diketahui :
- (f o g)(x) = 4x2 + 4x – 3
- (g o f)(x) = 2x2 – 7
Pembahasan
- (f o g)(x) = 4x2 + 4x – 3
f(g(x)) = 4x2 + 4x – 3
(g(x))2 – 4 = 4x2 + 4x – 3
(g(x))2 = 4x2 + 4x –3 + 4
(g(x))2 = 4x2 + 4x +1
(g(x))2 = (2x+1)2
g(x) = 2x+1
- Misal : g(x)=ax+b
g(f(x)) = 2x2 – 7
g(x2 – 4) = 2x2 – 7
a(x2 – 4) + b = 2x2 – 7
ax2 – 4a + b = 2x2 – 7
a = 2
– 4a + b = – 7
– 4.2 + b = – 7
– 8 + b = – 7
b = 8 – 7 = 1
Jadi, g(x) = ax+b = 2x+1
SIFAT-SIFAT OPERASI KOMPOSISI FUNGSI
Fungsi Komposisi memiliki beberapa sifat, diantaranya:
1). Tidak Berlaku Sifat Komutatif
(g o f)(x) tidak sama dengan (f o g)(x)
2). Berlaku Sifat Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)
3). Terdapat Fungsi Identitas f(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Materi Matematika Wajib SMA - 11 Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








