Peluang

Konsep Ruang Sampel

Sumber : pexels.com

Halo, Sobat Pintar!
Siapa yang kecilnya pernah bermain ular tangga atau monopoli? Pasti Sobat pernah bermain ular tangga atau monopoli dongg...
Kalau memainkan permainan tersebut, kalian pasti perlu menggulirkan dadu, kan? Hayoo ada berapa jumlah mata dadu yang ada di setiap sebuah dadu? Yapp, tepat sekali ada 6.
Di awal permainan, pasti kalian berharap mata dadu 6 muncul kan? Ternyata kita bisa menghitung peluang munculnya mata dadu 6 lho, Sobat! Setiap dadu yang muncul, kita dapat menghitung Peluangnya. Kira kira bagaimana yaa cara menghitungnya?

Nah, sebelum kita mempelajari materi Peluang lebih jauh, kalian harus tahu dulu apa istilah-istilah yang ada dalam peluang.

Percobaan
Percobaan adalah suatu kegiatan yang menghasilkan data. 
Beberapa contoh dari percobaan yaitu pelemparan koin, pelemparan dadu, serta pelemparan dadu dan koin.

Ruang Sampel
Ruang sampel adalah himpunan semua hasil yang mungkin terjadi pada suatu percobaan. 
Pada umumnya, ruang sampel dilambangkan dengan huruf S. Salah satu contoh ruang sampel dari pelemparan satu keping uang logam adalah {A, G} dengan A sebagai angka dan G sebagai gambar.

Titik Sampel
Titik sampel adalah hasil yang mungkin terjadi dari suatu percobaan. Titik sampel merupakan anggota-anggota dari ruang sampel. Banyaknya titik sampel pada suatu ruang sampel dapat dilambangkan dengan n(S). 
Contoh dari Ruang sampel : 
pada pelemparan sebuah dadu diperoleh titik sampel 1, 2, 3, 4, 5, dan 6 sehingga n(S)=6.

Kejadian
Kejadian merupakan himpunan bagian dari ruang sampel.
Contoh dari Kejadian ialah Misalnya jika sebuah dadu dilempar, akan ada kejadian dimana mata dadu yang terlihat adalah bilangan ganjil dengan ruang sampel {1,3,5}. 

Peluang Kejadian

Setelah kita mempelajari istilah-istilah dalam peluang, sekarang kita masuk ke dalam definisi dari Peluang.
Hayo, Sobat Pintar tahu engga apa itu peluang? Rumus dasar Peluang juga apaaa yaa? Daripada penasaran, langsung disimak aja yaa Sobat.
Semangat Sobat!

Misalkan A suatu kejadian yang merupakan himpunan bagian dari ruang sampel S. Artinya setiap anggota A juga merupakan anggota dari S (A subset S).

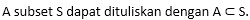
Maka peluang dapat dirumuskan sebagai berikut:

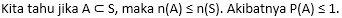
Terdapat beberapa kejadian khusus, yaitu:

Berdasarkan penjelasan diatas, maka besar nilai peluang suatu kejadian A adalah

Kejadian Tidak Saling Lepas

Halo Sobat Pintar, bagaimana dengan konsep dasar mengenai Peluang? Mudah bukan?
Nah, kita lanjut yuk ke materi peluang majemuk. Ada apa aja sih dalam peluang majemuk?
Dalam peluang majemuk ada beberapa kejadian, yaitu: kejadian tidak saling lepas, kejadian saling lepas, dan kejadian saling bebas serta kejadian bersyarat.

Dua kejadian yang dapat terjadi secara bersama-sama dikatakan kejadian tidak saling lepas.

Perhatikan diagram venn berikut!

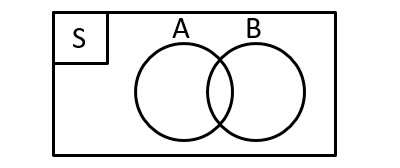
Misalkan kejadian A dan kejadian B berada pada ruang sampel S. Kejadian A dan B dikatakan tidak saling lepas jika terdapat minimal satu elemen pada kejadian A yang sama dengan elemen yang ada pada kejadian B.

Peluang kejadian A atau B yang mungkin terjadi dengan A dan B adalah kejadian tidak saling lepas, dapat dirumuskan sebagai berikut:

Misalnya akan diambil satu kartu bridge secara acak. Kejadian A adalah kejadian terambilnya kartu yang bergambar hati dan kejadian B terambilnya kartu J,Q,K. Terdapat kemungkinan terambil kartu Queen yang bergambar hati. Oleh karena itu, kejadian A dan B dapat dikatakan sebagai kejadian tidak saling lepas.