Kaidah Pencacahan

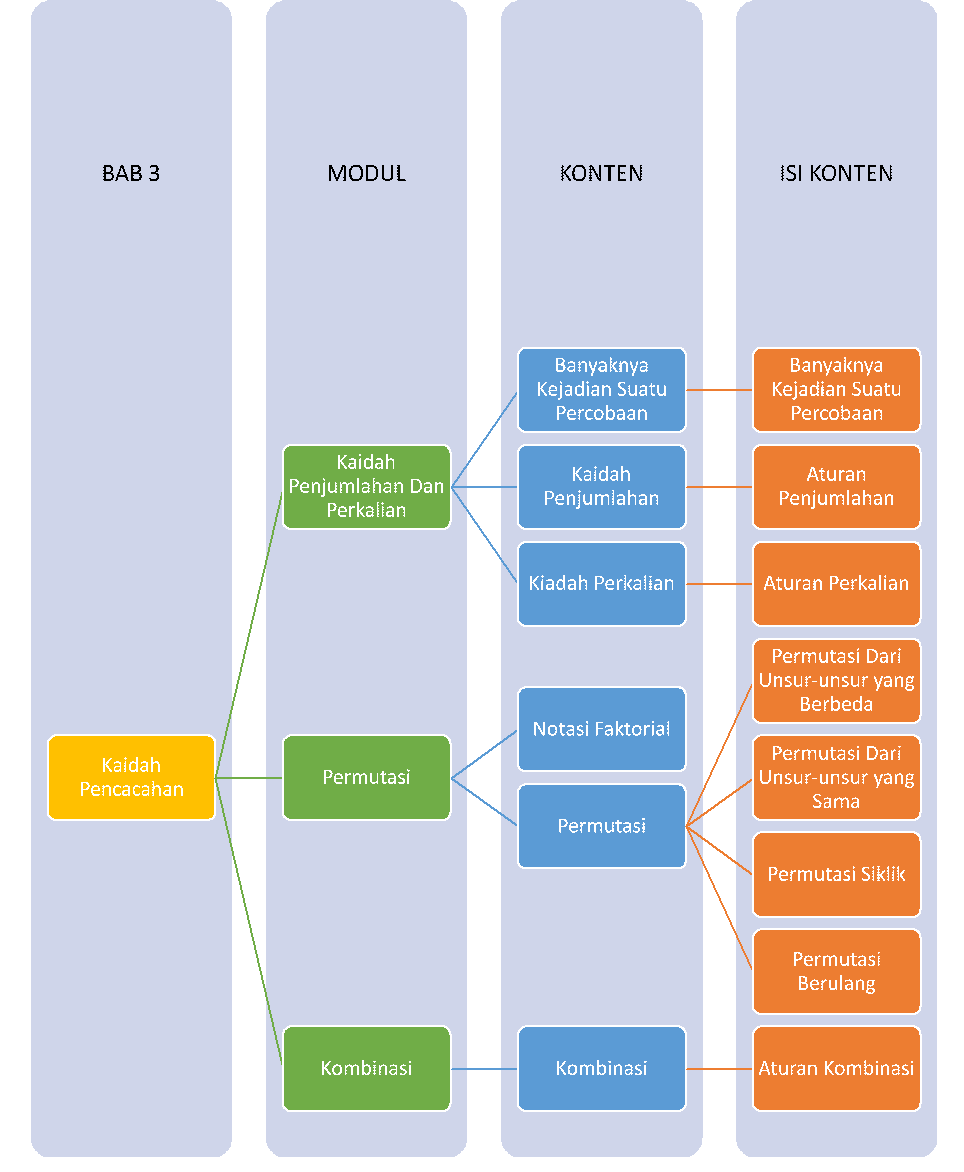
Kaidah Penjumlahan dan Perkalian

^{Sumber : Dekoruma.com}

Sobat Pintar, pasti pernah bingung ketika memilih pakaian, kan? Wah, sama dong! hihihi...

Materi yang akan kita pelajari kali ini akan berhubungan dengan pilih memilih nih. Yuk, kita belajar bersama tentang permutasi dan kombinasi.

Sebelum kita belajar teori permutasi dan kombinasi, kita perlu memahami dulu tentang kaidah penjumlahan dan perkalian. Eitsss, tapi sebelum itu kalian harus paham dulu tentang banyak kejadian suatu percobaan. Apa sih?

Setiap melakukan suatu percobaan pasti akan selalu mendapatkan hasil. Namun, tidak selalu hasil tersebut sesuai dengan yang diharapkan. Oleh karena itu dalam melakukan percobaan kita tentu harus menduga hasil yang mungkin terjadi. Dalam menentukan banyak kejadian suatu percobaan kita dapat menggunakan bantuan tabel dan diagram pohon.
 

Notasi Faktorial

^{Sumber : PNG Download.id}

Pernahkah Sobat Pintar duduk di meja bundar? Bagaimana kalian menentukan tempat duduknya? Kalau kamu ingin duduk di sebelah temanmu si A, tetapi si A ingin duduk di sebelah si B, bagaimana kemungkinan urutan tempat duduknya ya?

Banyaknya cara untuk duduk pada meja bundar dapat dihitung dengan menggunakan rumus permutasi lho, Sobat Pintar.

Dalam permutasi perlu dipahami terlebih dahulu terkait faktorial. Hasil kali bilangan bulat dari 1 sampai n adalah n! (dibaca : n faktorial) atau :

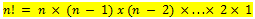
Contoh : 5! = 5 x 4 x 3 x 2 x 1 = 120

Kombinasi

^{Sumber : Kompasiana.com}

Menurut kalian pemilihan pemain sepak bola bagaimana ya, Sobat Pintar? Kita bisa menghitung banyaknya pemain terpilih menjadi pemain inti yang mungkin terbentuk dengan teori kombinasi lho, Sobat!

Sobat, setelah kita belajar tentang teori permutasi, kita beralih ke teori kombinasi.

Kombinasi adalah cara yang berbeda dalam memilih kelompok dengan mengambil beberapa atau semua anggota himpunan tanpa memperhatikan urutan.

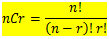
Sebagai ilustrasi : kombinasi 2 elemen dari 3 huruf a,b,c adalah ab, ac, bc . Sedangkan ba, ca, cb tidak termasuk hitungan karena pada kombinasi ab=ba, ac = ca, bc = cb. Banyak kombinasi adalah :

3C2 = 3! / 2! (3-2)! = 3!/2! = 3 x 2 x 1 / 2 x 1 = 3

Bagaimana sobat pintar, mudah ya... ?

Yuk kita latihan soal!