Materi Matematika Wajib - Statistika Kelas 12 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Hallo Sobat, berikut Peta Belajar Bersama materi Statistika yang akan kita pelajari
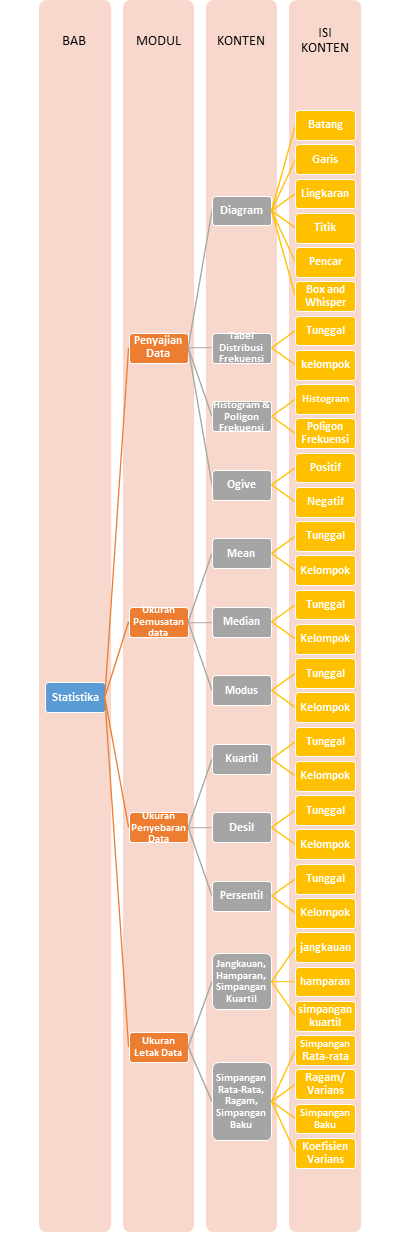
Yuk, kita belajar bersama-sama!
Penyajian Data dalam Bentuk Diagram

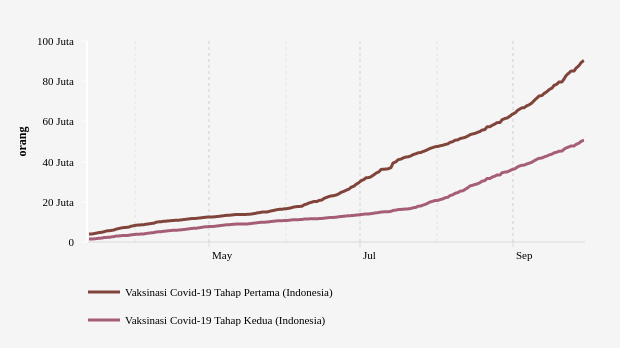
Sumber: databoks.katadata.co.id
Halo, Sobat Pintar! Apakah Sobat Pintar mengikuti perkembangan vaksinisasi yang sedang gencar diadakan oleh pemerintah?
Gambar diatas merupakan grafik perkembangan warga Indonesia yang sudah di vaksinisasi Covid-19 baik tahap 1 atau tahap 2 sampai dengan pertengahan bulan september 2021. Menurut sobat, berapa rata-rata warga Indonesia yang memperoleh vaksin tahap 1 setiap bulannya? Dan berapa rata-rata warga Indonesia yang memperoleh vaksin tahap 2 setiap bulannya? Kedua pertanyaan tersebut dapat kita jawab dengan memahami statistika lhoo, Sobat!
Yuk kita belajar bersama tentang statistika agar kita paham mengenai penyajian data.
Sobat Pintar sudah tau definisi Statistika belum?
Statistika ialah ilmu yang mempelajari tentang bagaimana merencanakan, menganalisis, menginterpretasi, mengumpulkan dan mempresentasikan data sehingga bisa dikatakan bahwa statistika merupakan ilmu yang berhubungan dengan data.
Terdapat banyak cara dalam menyajikan data dalam statistika, salah satunya penyajian data dalam bentuk diagram.
Berikut berbagai contoh diagram untuk menyajikan data dalam statistika
DIAGRAM GARIS
Penyajian data statistik dengan menggunakan diagram berbentuk garis lurus disebut diagram garis lurus atau diagram garis. Diagram garis biasanya digunakan untuk menyajikan data statistik yang diperoleh berdasarkan pengamatan dari waktu ke waktu secara berurutan.
Berikut contoh dari diagram garis:
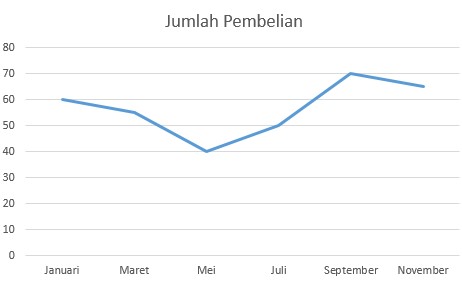
DIAGRAM BATANG
Diagram batang umumnya digunakan untuk menggambarkan perkembangan nilai suatu objek penelitian dalam kurun waktu tertentu. Diagram batang menunjukkan keterangan-keterangan dengan batang-batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah.
Berikut contoh dari diagram batang:
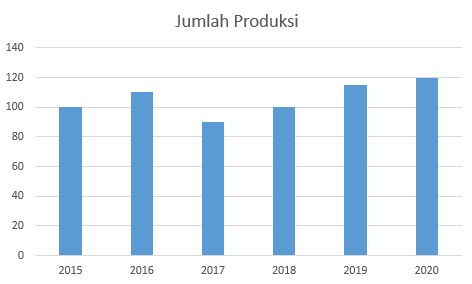
DIAGRAM LINGKARAN
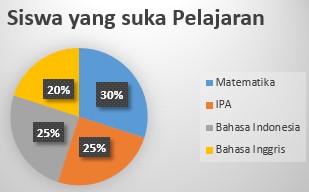
Diagram lingkaran adalah penyajian data statistik dengan menggunakan gambar yang berbentuk lingkaran. Bagian-bagian dari daerah lingkaran menunjukkan bagian-bagian atau persen dari keseluruhan. Untuk membuat diagram lingkaran, terlebih dahulu ditentukan besarnya persentase tiap objek terhadap keseluruhan data dan besarnya sudut pusat sektor lingkaran.
Berikut contoh dari diagram lingkaran:
Mean (Rata-Rata)


Sumber: republika.co.id
Pada gambar diatas, terlihat siswa sekolah dasar yang sedang berbaris dan terdiri dari berbagai macam tinggi badan ya, sobat! Siswa sekolah dasar memiliki bervariasi tinggi, dari yang paling depan terlihat paling pendek sampai dengan yang paling belakang terlihat semakin tinggi. Menurut Sobat, berapa rata-rata tinggi dari siswa sekolah dasar yang sedang berbaris?
Setelah kita mempelajari mengenai penyajian data, selanjutnya kita akan belajar tentang ukuran pemusatan data. Terdapat 3 ukuran pemusatan data dalam statistika yaitu mean (rata-rata), median (nilai tengah), dan modus (nilai yang sering muncul).
Pertama, kita akan membahas tentang mean (rata-rata)! Menurut sobat, rata-rata itu apa sihhh??
Rata-rata adalah perbandingan antara jumlah data dengan banyak data. Istilah rata-rata juga bisa disebut dengan mean dengan lambang 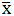
Rata-rata data tunggal dan rata-rata data kelompok dirumuskan sebagai berikut.
Rata-Rata Data Tunggal
Suatu data terdiri dari x1, x2, x3, … , xn, maka untuk rumus rata-rata dapat dirumuskan sebagai berikut:
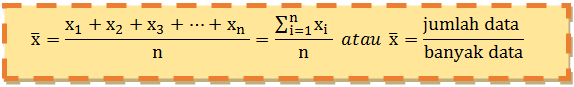

Suatu data disajikan dalam bentuk tabel distribusi frekuensi, maka rumus rata-rata dapat dirumuskan sebagai berikut:
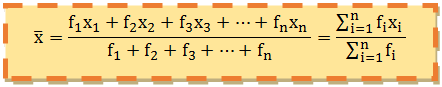

Rata-Rata Data Berkelompok
Rata-rata untuk data berkelompok sama dengan rata-rata data pada distribusi frekuensi tunggal yaitu dengan mengambil titik tengah atau nilai tengah setiap kelas sebagai xi. Rata-Rata data berkelompok dapat dirumuskan sebagai berikut:
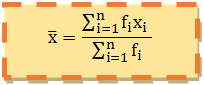

Kuartil


Source : id.lovepik.com
Wahhh, terlihat belasan orang sedang berbaris menuju ke loket ya, Sobat. Dari sekumpulan orang yang sedang berbaris tersebut, menurut Sobat orang yang menggunakan baju apa yaa yang berada di urutan tengah?
Kali ini, pembahasan kita berhubungan dengan letak atau urutan lohh, Sobat.
Setelah sebelumnya kita mempelajari tentang penyajian data dan ukuran pemusatan data, selanjutnya kita akan belajar tentang ukuran letak data. Ukuran letak data itu ada 3 loh Sobat Pintar. Apa saja ya? Ada Kuartil, Desil, dan juga Persentil. Kita bahas satu per satu yuk, Sobat!
Kuartil
Kuartil adalah nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama banyak. Karena membagi menjadi empat bagian sama banyak, artinya terdapat 3 nilai kuartil, yaitu Kuarti Bawah (Q1), Kuartil Tengah (Q2), dan Kuartil Atas (Q3).
Kuartil dapat digambarkan sebagai berikut:

- Kuartil Data Tunggal
Untuk data tunggal, kuartil dapat dirumuskan sebagai berikut:


- Kuartil Data Kelompok
Untuk data kelompok, kuartil dapat dirumuskan sebagai berikut:
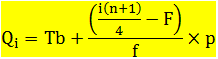

Jangkauan, Hamparan, dan Simpangan Kuartil

Halo Sobat Pintar! Setelah sebelumnya kita sudah membahas mengenai ukuran pemusatan data dan juga ukuran letak data, sekarang kita akan membahas mengenai ukuran penyebaran data. Sobat pintar sudah pernah mendengar mengenai ukuran penyebaran data?
Ukuran penyebaran data adalah suatu ukuran yang menyatakan seberapa besar nilai-nilai data berbeda atau bervariasi dengan nilai ukuran pusatnya atau seberapa besar penyimpangan nilai-nilai data dengan nilai pusatnya.
Menurut Sobat, apa saja ukuran penyebaran data? Yuk sama-sama kita pelajari!!
JANGKAUAN
Jangkauan (R) atau yang bisa disebut juga dengan range adalah selisih antara nilai data terbesar dan nilai data terkecil pada suatu data tunggal. Untuk sebaran data kelompok, nilai data terbesar diambil dari nilai tengah kelas tertinggi dan nilai data terkecil diambil dari nilai kelas yang terendah.
Jangkauan dapat dirumuskan sebagai berikut:

HAMPARAN
Hamparan (H) atau yang disebut juga dengan jangkauan antarkuartil adalah selisih antara nilai kuartil ketiga dan nilai kuartil pertama.
Hamparan dapat dirumuskan sebagai berikut:
H = Q3 - Q1
Keterangan:
H = hamparan
Q3 = nilai kuartil atas
Q1 = nilai kuartil bawah
SIMPANGAN KUARTIL
Simpangan kuartil (SK) atau yang disebut juga dengan jangkauan semi antarkuartil adalah setengah kali nilai hamparan.
Simpangan Kuartil dapat dirumuskan sebagai berikut:
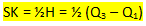
Keterangan :
SK = Simpangan Kuartil
H = Hamparan
Q3 = Nilai Kuartil Atas
Q1 = Nilai Kuartil Bawah
Materi Matematika Wajib SMA - 12 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








