Materi UTBK - SNBT - Pengetahuan Kuantitatif Kelas 12 MIA - Belajar Pintar
BelajarPintarV3
Himpunan dan Jenis Himpunan

Kelompok, kumpulan, kelas, maupun gerombolan dalam matematika dikenal dengan istilah himpunan. Namun, tidak semua kumpulan termasuk himpunan.
Kumpulan yang termasuk himpunan
- Kumpulan siswa yang lahir pada bulan Agustus
- Kumpulan siswa laki-laki
- Kumpulan buah-buahan yang diawali dengan huruf M
- Kumpulan nama kota di Indonesia yang diawali dengan huruf S
- Kumpulan binatang yang berkaki dua
- Kumpulan negara di Asia Tenggara
Kumpulan yang termasuk bukan himpunan
- Kumpulan kota-kota besar di Indonesia
- Kumpulan orang kaya di Indonesia
- Kumpulan siswa yang pandai di sekolahmu
- Kumpulan gunung yang tinggi di Indonesia
- Kumpulan pelajaran yang disenangi siswa
- Kumpulan makanan yang lezat
Dari contoh diatas maka bisa diambil kesimpulan bahwa yang termasuk Himpunan adalah kumpulan yang bisa diukur dan definisikan sama oleh semua orang.
Penyajian Himpunan
Sekarang kita lanjut memahami tentang penyajian himpunan.
Cara 1: Dinyatakan dengan menyebutkan anggotanya (enumerasi)
Suatu himpunan dapat dinyatakan dengan menyebutkan semua anggotanya yang dituliskan dalam kurung kurawal. Manakala banyak anggotanya sangat banyak, cara mendaftarkan ini biasanya dimodifikasi, yaitu diberi tanda tiga titik ("…") dengan pengertian “dan seterusnya mengikuti pola"
Cara 2: Dinyatakan dengan menuliskan sifat yang dimiliki anggotanya
Suatu himpunan dapat dinyatakan dengan menyebutkan sifat yang dimiliki anggotanya.
Cara 3: Dinyatakan dengan notasi pembentuk himpunan
Suatu himpunan dapat dinyatakan dengan menuliskan syarat keanggotaan himpunan tersebut.
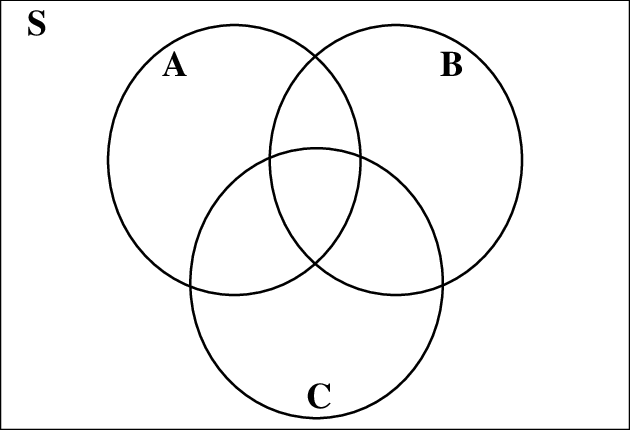
DIAGRAM VENN
Petunjuk dalam membuat diagram Venn antara lain:
- Himpunan semesta (S) digambarkan sebagai persegi panjang dan huruf S diletakkan di sudut kiri atas.
- Setiap himpunan yang ada dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
- Setiap anggota himpunan ditunjukkan dengan titik.
- Bila anggota suatu himpunan mempunyai banyak anggota, maka anggotaanggotanya tidak perlu dituliskan.
JENIS JENIS HIMPUNAN
Himpunan terbagi menjadi beberapa macam yaitu :
- Himpunan Semesta, himpunan yang anggotanya adalah seluruh semesta himpunan
- Himpunan Bagian, himpunan yang anggota sebagian dari anggota himpunan lain. Disimbolkan dengan tanda subset
- Himpunan Berhingga, himpunan yang anggotanya dapat dihitung
- Himpunan Tak Berhingga, himpunan yang anggotanya tak hingga banyak sehingga tidak dpaat dihitung
- Himpunan Kosong, himpunan yang tidak memiliki anggota, disimbolkan dengan tanda {} atau Ø
Fungsi

RELASI
Sobat pintar masih ingat tidak apa itu relasi?
Relasi menyatakan hubungan antara anggota himpunan dengan anggota himpunan lain. Himpunan A dan Himpunan B dikatakan memiliki relasi jika terdapat anggota himpunan yang saling berpasangan dengan hubungan tertentu
Relasi antara dua himpunan dapat dinyatakan dengan tiga cara yaitu:
a) Diagram Panah
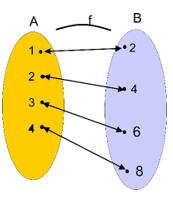
b) Himpunan Pasangan Berurutan
K = {(1,2),(2,4),(3,6),(4,8),(5,10)
c) Diagram Kartesius
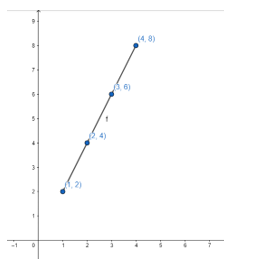
FUNGSI
Fungsi (pemetaan) adalah relasi dari himpunan A ke himpunan B, jika terdapat setiap anggota berpasangan tepat satu anggota himpunan B. Semua anggota himpunan A disebut domain (daerah asal), semua anggota himpunan B disebut kodomain (daerah kawan) dan hasil dari pemetaan himpunan A dan himpunan B adalah daerah hasil (range). Sama seperti relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, diagram kartesius, dan himpunan pasangan berurutan
Suatu fungsi secara sistematis dapat dituliskan:
f:x -> ax+b (fungsi f memetakan x ke ax+b)
atau
f(x) = ax+b (fungsi dalam x)
atau
y= ax+b (y adalah fungsi dari x)
Catatan
Jika f(x)=y, maka y merupakan bayangan x (image), sedangkan x merupakan prabayangan dari y (pra-image)
Fungsi dapat disajikan dalam bentuk:
- diagram panah
- diagram cartesius
- himpunan pasangan berurutan
DOMAIN, KODOMAIN DAN RANGE FUNGSI
Jika f adalah suatu fungsi dari A ke B, maka himpunan A disebut domain (daerah asal) dan himpunan B disebut kodomain (daerah kawan). Sedangkan himpunan B yang berpasangan (himpunan C) disebut range (hasil) fungsi f.
Aturan yang memasangkan anggota himpunan A dengan anggota-anggota himpunan B disebut aturan fungsi f.
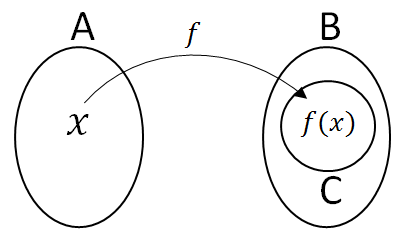
Domain suatu fungsi dapat ditetapkan secara jelas (eksplisit). Jika domain tidak ditetakan dengan jelas, maka digunakan kesepakatan bahwa domainnya merupakan himpunan bilangan real.
Syarat yang harus dipenuhi agar suatu fungsi terdefinisi (memiliki daerah hasil di himpunan bilangan real), yaitu:
- fungsi dalam akar
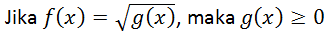
- fungsi pecahan
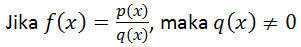
- fungsi pecahan, dimana penyebutnya merupakan fungsi lain dalam bentuk akar
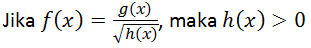
- fungsi logaritma
Jika f(x) = g(x) log h(x), maka h(x)>0, g(x)>0 dan g(x) tidak sama dengan 1
GRAFIK FUNGSI
Suatu fungsi dari himpunan A ke himpunan B dapat dbuat grafik pemetaannya dengan menggunakan diagram cartesius. Grafik suatu fungsi dapat berupa garis lurus maupun kurva.
Langkah-langkah menggambar grafik fungsi pada koordinat cartesius, yaitu:
- Tentukan domain (jika belum diketahui secara pasti, pilih beberapa bilangan bulat disekitar nol)
- Tentukan pasangan berurutan dari fungsi tersebut
- Gambar pasangan berurutan sebagai titik pada koordinat cartesius
- Hubungkan titik-titik yang sudah digambar pada koordinat cartesius
Berdasarkan grafik suatu fungsi, dapat ditentukan domain dan range nya. Domain fungsi terletak pada sumbu x, sedangkan kodomain fungsi terletak pada sumbu y.
OPERASI ALJABAR FUNGSI
Pada dua atau lebih fungsi dapat dilakukan operasi aljabar seperti penjumlahan, pengurangan, perkalian dan pembagian.
Operasi aljabar yang berlaku pada fungsi, antara lain:

Bilangan Rasional


Hai Sobat Pintar, mari kita perhatikan tabel di atas. Apakah kalian bisa melihat kaitan antara jenis bilangan yang satu dengan yang lain? Tampak bilangan asli termasuk dalam kategori bilangan cacah, dan bilangan cacah juga merupakan bagian dari bilangan bulat. Berikut adalah gambaran visualnya menggunakan diagram Venn.
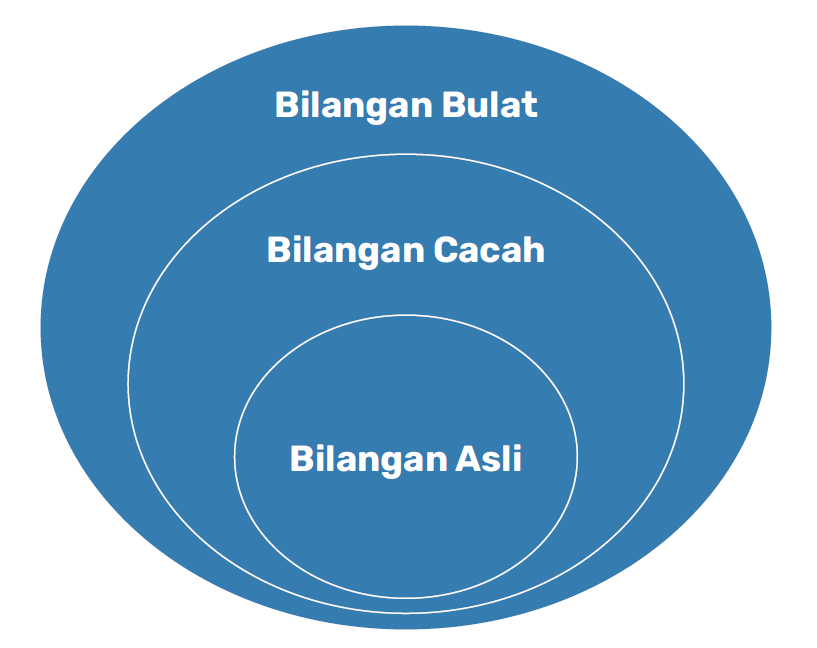
Dalam rangkaian dua bilangan bulat, terdapat sebuah bilangan lain yang tidak termasuk dalam kategori bilangan bulat. Bilangan itu disebut Bilangan Rasional. Sobat Pintar tau nggak apa definisi bilangan rasional? Bilangan rasional merujuk pada suatu bilangan yang dapat diwakili dalam bentuk pecahan biasa (a/b), dan jika dinyatakan dalam bentuk desimal, angkanya akan berhenti setelah sejumlah digit atau akan membentuk pola pengulangan.
Untuk menentukan apakah suatu bilangan adalah bilangan rasional atau tidak, salah satu metode yang dapat digunakan adalah dengan mengubahnya menjadi pecahan a/b, di mana a adalah pembilang dan b adalah penyebut.
Bagaimana sobat menyatakan −0,5 dalam (a/b)? Bisa jadi ada yang menuliskan −1/2, 1/−2, atau bentuk lain yang ekuivalen. Ketiga penulisan tersebut berbeda, namun menyatakan bilangan rasional yang sama. Sebuah bilangan rasional dapat dinyatakan dengan banyak cara penulisan (a/b).
Bilangan rasional juga dapat dinyatakan dalam bentuk desimal. Apakah semua bilangan desimal merupakan bilangan rasional? Coba perhatikan contoh berikut:
akar 2 = 1,414213562 . . .
phi = 3,141592564 . . .
keduanya memiliki angka desimal yang tak terbatas.
Bilangan akar 2 dan phi termasuk ke dalam bilangan irasional. Kalian akan mempelajari bilangan irasional di tingkat berikutnya. Bilangan Rasional dan Irasional termasuk ke dalam Bilangan Real.
Operasi bilangan rasional
Penjumlahan dan Pengurangan bilangan rasional harus disamakan terlebih dahulu penyebutnya.
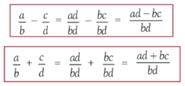
Sedangkan perkalian dan pembagian bilangan rasional tidak perlu disamakan penyebutnya
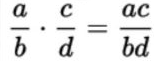
Untuk pembagian bilangan rasional, dapat berubah menjadi perkalian dengan syarat penyebut dan pembilang pembaginya harus bertukar.
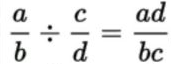
Bentuk Umum dan Penyelesaian Persamaan Kuadrat

Persamaan kuadrat adalah persamaan polinom berderajat dua. Bentuk umum persamaan kuadrat dituliskan sebagai ax2 + bx + c = 0 atau dalam bentuk fungsi kuadrat adalah y = ax2 + bx + c.
Keterangan:
x = variabel
a = koefisien kuadrat dari x2
b = koefisien linear dari x
c = konstanta
Akar-akar persamaan kuadrat ax2 + bx + c = 0 merupakan nilai variabel x sehingga persamaan kuadrat bernilai benar. Akar-akar suatu persamaan kuadrat maskimal ada dua.
Pada grafik fungsi kuadrat, jika x1 dan x2 adalah akar-akar persamaan kuadrat, maka titik-titik dengan koordinat (x1, 0) dan (x2, 0) merupakan titik potong kurva persamaan kuadrat dengan sumbu x.
Mencari akar-akar dalam menyelesaikan persamaan kuadrat dilakukan dengan 3 cara sebagai berikut.
1. Faktorisasi
Faktorisasi atau pemfaktoran merupakan cara mencari akar-akar persamaan kuadrat dengan mencari nilai yang jika dikalikan akan menghasilkan nilai lain. Ada tiga bentuk persamaan kuadrat dengan faktorisasi akar-akar yang berbeda seperti berikut:
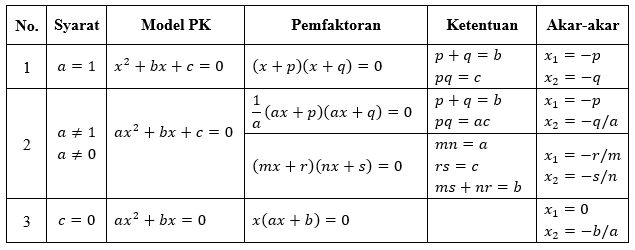
Contoh Soal :
Tentukan akar-akar persamaan kuadrat x2 – 6x + 8 = 0!
Pembahasan :
x2 – 6x + 8 = 0
(x – 2)(x – 4) = 0
x – 2 = 0 atau x – 4 = 0
x = 2 x = 4
Jadi, akar-akar persamaan kuadrat x2 – 6x + 8 = 0 adalah x1 = 2 dan x2 = 4
2. Kuadrat Sempurna
Tidak semua persamaan kuadrat bisa diselesaikan dengan cara faktorisasi, cara lain untuk menyelesaikan persamaan kuadrat dengan cara melengkapkan kuadrat sempurna.
Bentuk persamaan kuadrat sempurna adalah bentuk persamaan yang menghasilkan bilangan rasional. Penyelesaian persamaan kuadrat dengan melengkapkan kuadrat menggunakan rumus:
(x + p)2 = x2 + 2px + p2
Ubah menjadi bentuk persamaan dalam (x+p)2 = q
Pembahasan :
(x + p)2 = q
x + p = + q
x = -p + q
Contoh Soal :
Tentukan akar-akar persamaan kuadrat x2 – 6x + 8 = 0!
Pembahasan :
x2 – 6x + 8 = 0
x2 – 6x = –8
x2 – 6x +... = –8 + ...
x2 – 6x + 9 = –8 + 9
(x – 3)2 = 1
x – 3) =+ 1
Jika x – 3 = –1 dan jika x – 3 = 1
x = –1 + 3 x = 1 + 3
x = 2 x = 4
Jadi, akar-akar persamaan kuadrat x2 – 6x + 8 = 0 adalah x1 = 2 dan x2 = 4
3. Rumus Kuadrat (Rumus abc)
Selain menggunakan faktorisasi dan dengan melengkapi kuadrat sempurna, persamaan kuadrat dapat diselesaikan dengan menggunakan rumus kuadrat atau biasa dikenal dengan rumus abc.
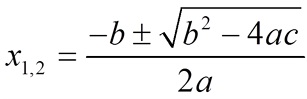
Bentuk b2 - 4ac dinamakan dengan Deskriminan (D)
Contoh soal :
Tentukan akar-akar persamaan x2 – 6x + 8 = 0!
Pembahasan :
Diketahui a = 1, b = –6, c = 8
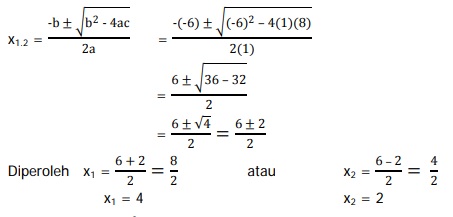
Jadi, akar-akar persamaan kuadrat x2 – 6x + 8 = 0 adalah x1 = 4 dan x2 = 2
Bentuk Umum dan Grafik Fungsi Kuadrat

Fungsi kuadrat merupakan fungsi yang berbentuk y = ax2 + bx + c, dengan a tidak sama dengan 0.
Grafik dari fungsi kuadrat menyerupai parabola, sehingga dapat dikatakan juga sebagai fungsi parabola.
Berikut merupakan gambar perbandingan grafik fungsi kuadrat y=x2 , y = -x2, dan y = 2x2.
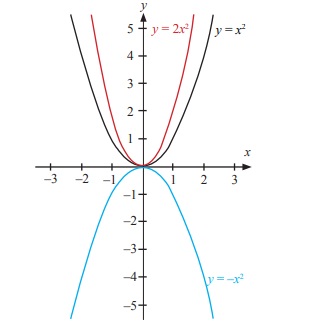
Nilai a pada fungsi y = ax2 + bx + c akan mempengaruhi bentuk grafiknya.
Jika a positif maka grafiknya akan terbuka ke atas. Sebaliknya jika a negatif maka grafiknya akan terbuka ke bawah. Jika nilai a semakin besar maka grafiknya menjadi lebih “kurus”.
Berikut merupakan perbandingan grafik fungsi kuadrat y = x2 + 2x, y = x2 – 3x + 2 dan y = –x2 – 5x – 4.
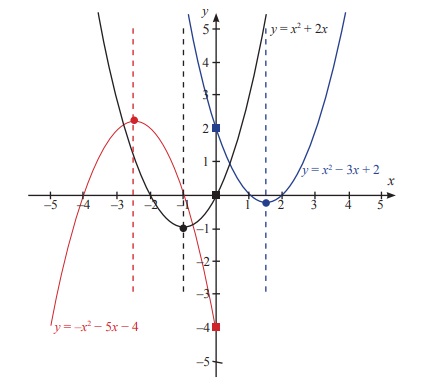
Garis putus-putus pada gambar di atas menerupakan sumbu simetri. Koordinat yang ditandai dengan bulatan merupakan titik puncak sedangkan koordinat yang ditandai dengan persegi merupakan titik potong dengan sumbu-y.
Nilai b pada grafik y = ax2 + bx + c menunjukkan letak koordinat titik puncak dan sumbu simetri (titik puncak dan sumbu simetri dibahas lebih lanjut pada subbab selanjutnya).
Jika a > 0, grafik y = ax2 + bx + c memiliki titik puncak minimum.
Jika a < 0, grafik y = ax2 + bx + c memiliki titik puncak maksimum.
Nilai c pada grafik y = ax2 + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu-y, yakni pada koordinat (0, c).
Pola Bilangan

Pola bilangan yaitu aturan yang digunakan untuk membuat suatu kelompok bilangan.
Macam-macam Pola Bilangan
Pola bilangan dapat dikelompokkan menjadi beberapa macam, diantaranya:
a. Pola Bilangan Ganjil
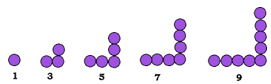
Berdasarkan pola di atas, terbentuk pola bilangan ganjil yaitu 1, 3, 5, 7, 9.
Rumus bilangan ke-n pada pola bilangan ganjil, yaitu 2n – 1
Sedangkan jumlah n bilangan ganjil pertama, yaitu n2
b. Pola Bilangan Genap

Berdasarkan pola di atas, terbentuk pola bilangan genap yaitu 2, 4, 6, 8.
Rumus bilangan ke-n pada pola bilangan genap, yaitu 2n.
Sedangkan jumlah n bilangan genap pertama, yaitu n(n+1).
c. Pola Garis Lurus
Pola garis lurus yaitu suatu bilangan yang digambarkan dengan noktah mengikuti pola garis lurus.
Contoh :

d. Pola Persegi Panjang
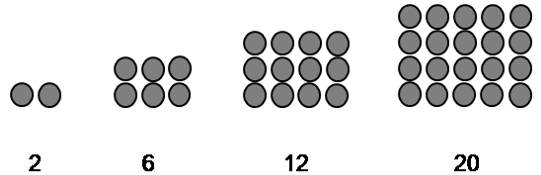
Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20.
Rumus bilangan ke-n pada pola persegi panjang, yaitu n(n+1).
Sedangkan jumlah n suku pertamanya, yaitu:
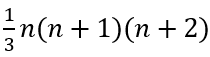
e. Pola Bilangan Persegi
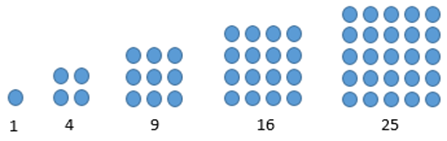
Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20.
Rumus bilangan ke-n pada pola persegi panjang, yaitu n(n+1).
Sedangkan jumlah n suku pertamanya, yaitu:
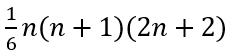
f. Pola Bilangan Segitiga

Berdasarkan pola di atas, terbentuk pola segitiga dengan susunan bilangan 2, 6, 12, 20.
Rumus bilangan ke-n pada pola persegi panjang, yaitu n2.
Sedangkan jumlah n suku pertamanya, yaitu:
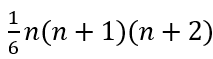
g. Pola Bilangan Pascal
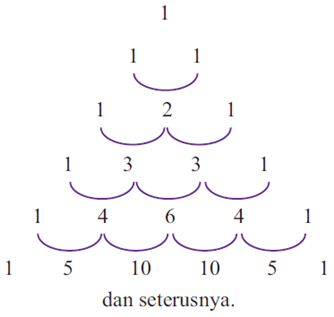
Pola di atas merupakan pola dari segitiga pascal. Segitiga pascal digunakan untuk menentukan koefisien dari polinomial.
Koefisiennya dapat ditentukan dengan rumus : (a+b)n.
Sedangkan jumlah bilangan pada segitiga pascal baris ke-n, yaitu 2n-1
Titik dan Garis


Sumber : AnakTeknik
Pernahkah kalian melihat burung yang bertengger pada kabel listrik? Kalau seandainya burung itu kita andaikan sebagai titik, kabel listrik sebagai garis, dan daratan sebagai bidang, maka kedudukan dari titik akan berubah-ubah bukan? Seperti burung yang bisa terbang, bertengger di kabel listrik maupun turun ke daratan. Nah! Kali ini, kita akan belajar bersama mengenai kedudukan titik, garis, dan bidang.
Halo, Sobat Pintar!! Pasti kalian tidak asing lagi dengan titik.
Titik yaitu suatu noktah yang hanya ditentukan letaknya, dan tidak mempunyai ukuran. Biasanya ditandai dengan huruf kapital, misalnya titik A, titik B, titik P, titik Q, dan seterusnya.
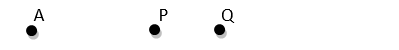
Kedudukan Titik terhadap Titik

Titik A terpisah dengan titik B, jadi titik A dan B adalah dua titik yang berbeda. Sedangkan titik B berimpit dengan titik C sehingga titik B = titik C.
Kedudukan Titik terhadap Garis
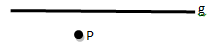
- Sebuah titik P dikatakan terletak pada garis g, jika garis g melalui titik P.

- Sebuah titik P dikatakan diluar garis g, jika garis g tidak melalui titik P.
Kedudukan Titik terhadap Bidang
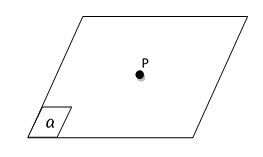
- Sebuah titik P dikatakan terletak pada bidang a, jika bidang a melalui titik P
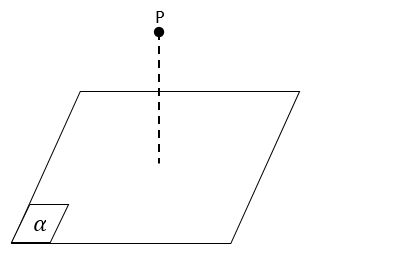
- Sebuah titik P dikatakan diluar bidang a, jika bidang a tidak melalui titik P
Gimana nih Sobat materi sebelumnya? Mudah bukan? Yuk kita beralih ke materi kedudukan garis!
Pada kedudukan garis ini terbagi menjadi dua sebagai berikut.
Kedudukan Dua Garis
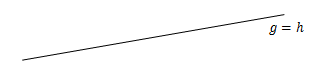
- Garis g dan garis h dikatakan berimpit jika setiap titik pada garis g juga terletak pada garis h, dan sebaliknya.
- Garis g dan garis h dikatakan saling berpotongan jika kedua garis tersebut memiliki satu titik persekutuan yang disebut titik potong. Dua garis hanya dapat berpotongan jika terletak pada suatu bidang yang sama.
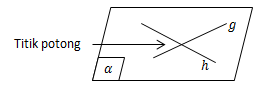
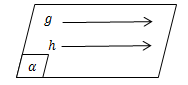
- Garis g dan garis h dikatakan sejajar jika kedua garis tidak memiliki titik persekutuan.
- Garis g dan garis h di katakan bersilangan jika kedua garis tidak memiliki titik persekutuan, tidak sejajar dan tidak terletak pada satu bidang yang sama.
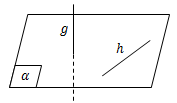
Kedudukan Garis dan Bidang
- Garis g dikatakan terletak pada bidang a jika paling sedikit dua titik pada garis g terletak pada bidang a
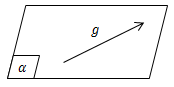
- Garis g dikatakan sejajar bidang a jika garis g sejajar dengan garis pada bidang a
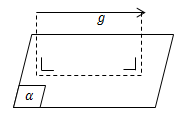
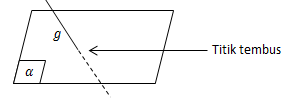
- Garis g dikatakan menembus bidang a jika garis g tidak terletak pada bidang dan tidak sejajar bidang a. Dalam hal ini, garis g dan bidang a mempunyai satu titik persekutuan yang dinamakan titik tembus.
Persamaan Lingkaran

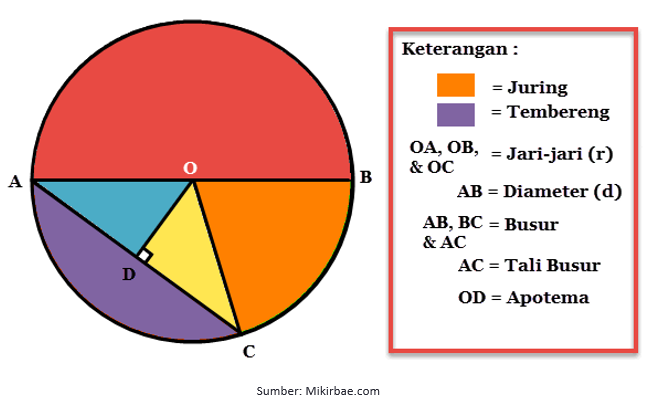
Sobat Pintar masih ingat atau tidak, apa sih pengertian dari lingkaran itu?
Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu. Yang dimaksud titik tertentu adalah titik pusat, sedangkan jarak yang sama adalah jari-jari lingkaran.
Sama halnya dengan gelombang sinus yang memiliki persamaan, lingkaran juga memiliki persamaan.
Bagaimana persamaannya?
Persamaan lingkaran dapat ditentukan jika diketahui titik pusat dan jari-jari lingkarannya.
LINGKARAN DENGAN PUSAT DI TITIK O(0,0)
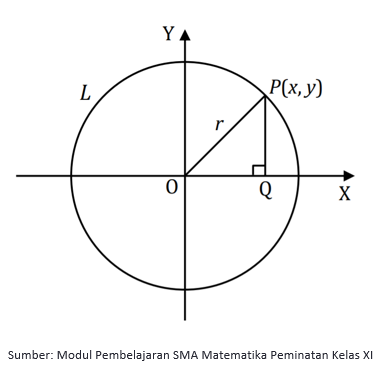
Perhatikan gambar di atas!
Lingkaran L berpusat di O(0, 0) dan berjari-jari r.
Misal titik P(x, y) adalah sebarang titik yang terletak pada lingkaran L, panjang ruas garis OP akan sama dengan jari-jari
Dapat dibentuk segitiga POQ siku-siku di Q, berdasarkan teorema pythagoras diperoleh:
OQ2 + PQ2 = OP2
Dari sini didapatkan persamaan lingkaran yang berpusat di titik O(0,0) dan berjari-jari r:
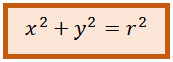
LINGKARAN DENGAN PUSAT DI TITIK M(a,b)
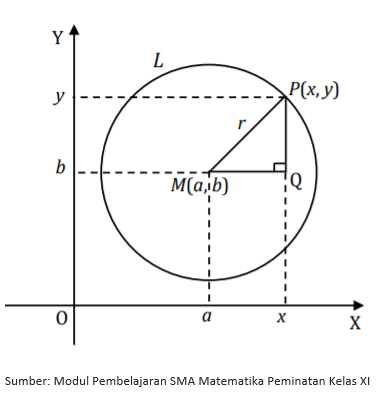
Perhatikan gambar di atas!
Lingkaran L berpusat di titik M(a, b) dengan jari-jari r.
Misal titik P(x, y) adalah sembarang titik yang terletak pada lingkaran L, maka
MP = r
MQ = x – a
PQ = y – b
Dengan informasi di atas dan segitiga PMQ, kita bisa menggunakan teorema pythagoras dan mendapatkan persamaan lingkaran yang berpusat di titik M(a, b) dan berjari-jari r
MQ2 + PQ2 = MP2
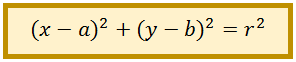
BENTUK UMUM PERSAMAAN LINGKARAN
Bentuk umum persamaan lingkaran yang berpusat di titik M(a,b) dengan jari-jari r dapat dicari dengan cara berikut:
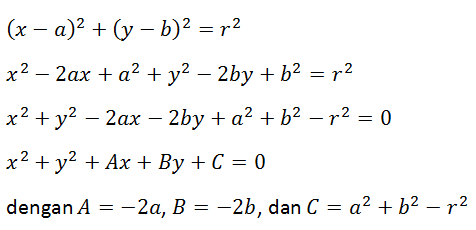
Jadi, bentuk umum dari persamaan lingkaran, yaitu:

RUMUS PENTING
Jarak dua titik
Misalkan diketahui titik A(xa,ya) dan titik B(xb, yb), maka jarak titik AB, yaitu:
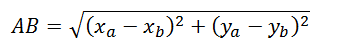
Jarak titik dengan garis
Misalkan diketahui titik C(xc, yc) dan garis Ax + By + C = 0, maka jarak titik C ke garis tersebut, yaitu:
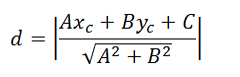
Konsep dan Sifat-Sifat Eksponen

Pangkat yang disebut juga sebagai Eksponen merupakan perkalian berulang dari sebuah bilangan real. Bilangan yang berpangkat bulat meliputi bilangan dengan pangkat bulat positif, pangkat bulat negatif dan pangkat nol. Yuk simak penjelasan setiap kelompoknya di bawah ini!
PANGKAT BILANGAN BULAT POSITIF
Secara matematis, bilangan berpangkat bilangan bulat positif dapat didefinisikan sebagai berikut:

PANGKAT BILANGAN BULAT NEGATIF DAN NOL
Secara umum, bilangan berpangkat bilangan bulat negatif dapat didefinisikan sebagai berikut:

Sedangkan bilangan dengan pangkat 0 dapat ditentukan:

Catatan:
Jika a=0, maka pangkat 0 tidak memiliki arti, karena:
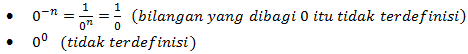
PANGKAT BILANGAN PECAHAN
Bilangan dengan pangkat bilangan pecahan seringkali dikaitkan dengan bentuk akar bilangan positif.
Pengubahan bentuk pangkat pecahan ke bentuk akar maupun sebaliknya menggunakan aturan berikut:
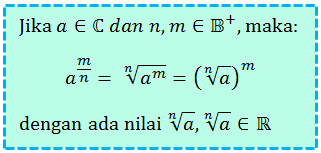
NOTASI ILMIAH EKSPONEN
Notasi ilmiah sangat bermanfaat untuk menuliskan secara singkat bilangan-bilangan yang sangat besar maupun sangat kecil.
Notasi ilmiah atau yang bisa disebut juga dengan bentuk baku dari suatu bilangan dapat dituliskan secara singkat dalam bentuk:
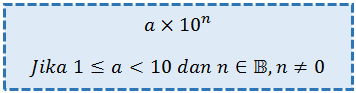
Catatan:
10-n berarti terdapat n angka di belakang koma, misal 10-3 = 0,001.
SIFAT-SIFAT EKSPONEN
Ketika melakukan operasi aljabar pada bilangan berpangkat bilangan bulat, kita dapat menggunakan sifat-sifat berikut:

Konsep dan Sifat-Sifat Logaritma

Logaritma merupakan suatu operasi yang berkebalikan dengan eksponen (perpangkatan). Logaritma dapat didefinisikan sebagai berikut:
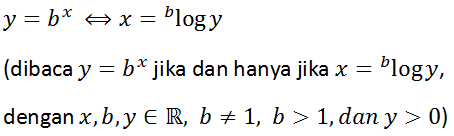
Catatan:
- b disebut bilangan pokok
- Jika bilangan pokoknya bernilai 10, biasanya tidak ditulis, misal 10log y = log y
- Jika bilangan pokoknya e (bilangan euler, e = 2,718281828...), maka bentuk logaritmanya ditulis dengan ln (dibaca: lon, merupakan logaritma natural), misal elog y = ln y
SIFAT-SIFAT FUNGSI LOGARITMA
Oleh karena bentuk logaritma masih berhubungan dengan pangkat, maka sifat-sifat logaritma dapat diturunkan dari sifat bilangan berpangkat, yaitu:
PERKALIAN LOGARITMA
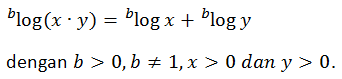
PEMBAGIAN LOGARITMA
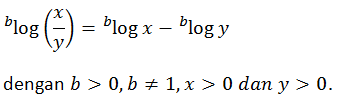
LOGARITMA DENGAN PANGKAT
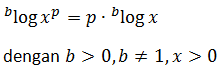
Sifat perpangkatan logaritma dapat diturunkan menjadi beberapa sifat berikut:
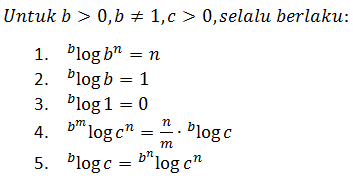
MENGUBAH BASIS LOGARITMA
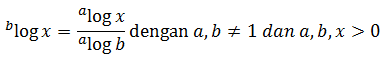
Berdasarkan sifat di atas, dapat diturunkan sifat berikut:
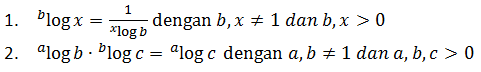
PERPANGKATAN LOGARITMA
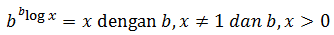
Konsep Matriks

Matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris (jajaran) dan kolom (lajur) dengan dibatasi oleh kurung biasa “( )” atau kurung siku “[ ]”.
Bilangan-bilangan yang tersusun dalam matriks disebut elemen (unsur) matriks. Baris sebuah matriks adalah susunan bilangan-bilangan yang mendatar (horizontal), sedangkan kolom adalah susunan bilangan-bilangan yang tegak (vertikal).
Jika suatu matriks diberi nama matriks A, maka secara umum, bentuk matriks A, yaitu:
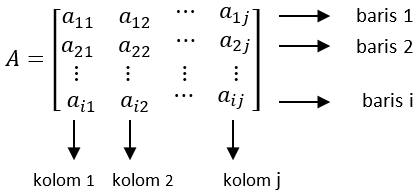
Amxn artinya matriks A mempunyai baris sebanyak m dan mempunyai kolom sebanyak n.
a11 = elemen baris pertama kolom pertama
a12 = elemen baris pertama kolom kedua
a1n = elemen baris pertama kolom ke-n
a21 = elemen baris kedua kolom pertama
...
amn = elemen baris ke-m kolom ke-n
ORDO MATRIKS
Ordo matriks adalah banyaknya elemen baris dan banyaknya elemen kolom dari suatu matriks. Jika sebuah matriks memiliki m baris dan n kolom, maka matriks tersebut berordo m x n, dapat dituliskan Amxn.
Contoh :

JENIS-JENIS MATRIKS
Matriks dapat dikelompokkan menjadi beberapa jenis sebagai berikut:
- Matriks nol, yaitu: matriks yang seluruh elemennya bilangan nol.
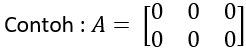
- Matriks baris, yaitu: matriks yang hanya memiliki satu baris atau berordo 1 x n.
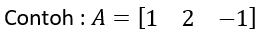
- Matriks kolom, yaitu: matriks yang hanya memiliki satu kolom atau berordo m x 1.
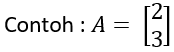
- Matriks persegi, yaitu: matriks yang banyaknya baris dan kolom sama atau berordo m x m.
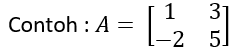
- Matriks diagonal, yaitu: matriks persegi yang semua elemennya nol, kecuali elemen pada diagonal utamanya bukan nol.
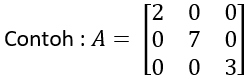
- Matriks segitiga atas, yaitu: matriks persegi yang semua elemen di bawah diagonal utamanya adalah nol.
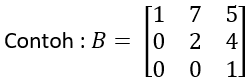
- Matriks segitiga bawah, yaitu: matriks persegi yang semua elemen di atas diagonal utamanya adalah nol.
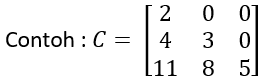
- Matriks identitas, yaitu: matriks persegi yang elemen pada diagonal utamanya adalah satu, sedangkan elemen lainnya adalah nol. Matriks identitas dilambangkan dengan “I”.
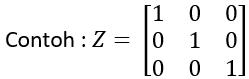
KESAMAAN DUA MATRIKS
Dua matriks dikatakan sama (A=B), apabila mempunyai ordo yang sama dan elemen-elemen yang letaknya sama (bersesuaian) besarnya sama atau aij = bij.
Contoh :
![]()
Matriks A=B karena ordo dan elemen yang letaknya bersesuaian besarnya sama. Matriks C=D karena ordo dan elemen yang seletak dari kedua matriks sama.
Matriks A≠C karena meskipun memiliki ordo yang sama, tetapi letak elemen yang sama tidak sesuai.
Definisi dan Ukuran Pemusatan Data

Statistika adalah ilmu yang mempelajari tentang bagaimana merencanakan, menganalisis, menginterpretasi, mengumpulkan dan mempresentasikan data sehingga bisa dikatakan bahwa statistika merupakan ilmu yang berkenaan dengan data. Datum adalah informasi yang diperoleh dari suatu pengamatan. Sedangkan data adalah kumpulan dari datum.
Ukuran pemusatan data terbagi menjadi tiga, yaitu rata-rata (mean), nilai tengah (median), dan modus.
Mean (rata-rata)
Rata-rata suatu data dapat diperoleh dengan menjumlahkan seluruh data kemudian dibagi dengan banyak datanya. Secara matematis, dapat dirumuskan:
1. Data tunggal
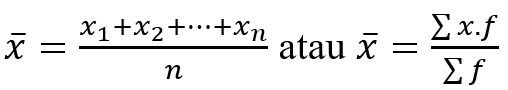
2. Data kelompok

Median (nilai tengah)
Median merupakan nilai tengah dari suatu data. Cara menentukan median pada data tunggal dan data kelompok berbeda. Namun, sebelum menentukan median, kita harus menentukan letak median terlebih dahulu, baik pada data tunggal maupun data kelompok.
Menentukan letak median
- banyaknya data berjumlah genap :
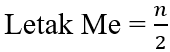
- banyaknya data berjumlah ganjil :
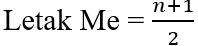
Setelah menentukan letak median, kita bisa mencari nilai median berdasarkan jenis datanya, yaitu
1. Data tunggal
Cara menentukan median pada data tunggal adalah dengan mengurutkan data dari yang terkecil hingga yang terbesar. Kemudian, hitunglah sejumlah letak median yang diperoleh.
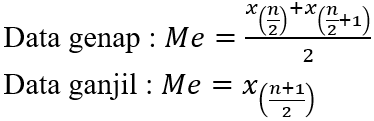
2. Data kelompok
Cara menentukan median pada data kelompok setelah mengetahui letak median, yaitu dengan menentukan kelas mediannya. Kemudian substitusikan pada rumus berikut:
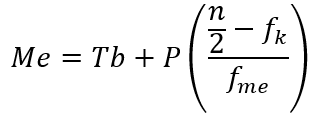
Keterangan :
Me = median
Tb = Tepi bawah kelas median – 0,5
P = panjang kelas median
n = frekuensi seluruh data
fk = frekuensi kumulatif sebelum kelas median
fme = frekuensi di kelas median
Modus
Modus merupakan datum yang paling sering muncul pada suatu data. Untuk menentukan modus pada data tunggal, hanya dengan menghitung frekuensi munculnya datum. Datum yang memiliki frekuensi terbanyak merupakan modus dari data tersebut.
Sedangkan modus pada data kelompok dapat ditentukan dengan cara berikut:
1. Tentukan kelas dengan frekuensi terbanyak, kelas tersebut merupakan kelas modus
2. Hitung nilai modus dengan rumus:
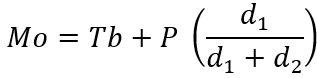
Keterangan :
Mo = Modus
Tb = tepi bawa kelas modus – 0,5
P = panjang kelas modus
d1 = selisih frekuensi kelas modus dengan kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan kelas setelahnya
Permutasi

Permutasi adalah susunan berurutan dari semua atau sebagian elemen dari suatu himpunan.
Untuk menyelesaikan soal permutasi terdapat 4 metode, yaitu:
Permutasi dari Elemen yang Berbeda
Permutasi elemen dari elemen yang ada (setiap elemen berbeda) adalah susunan elemen itu dalam suatu urutan yang diperhatikan. Banyaknya permutasi dari elemen n diambil r elemen dapat dinotasikan:
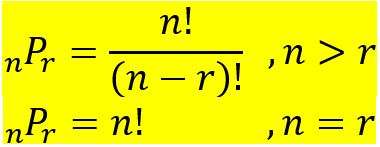
Permutasi dengan Berapa Elemen yang Sama
Setiap unsur yang digunakan tidak boleh lebih dari satu kali. Secara umum, banyaknya permutasi n elemen yang memuat k, l, m, … elemen yang sama dapat dinotasikan:
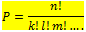
Permutasi Siklis
Permutasi siklis digunakan untuk menghitung banyak cara yang dibuat dari susunan melingkar. Secara umum, banyaknya permutasi siklis dapat dinotasikan:
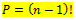
Permutasi Berulang
Permutasi berulang adalah permutasi yang dalam penyusunannya urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali (berulang). Banyaknya permutasi ini dinotasikan:
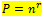
Sedangkan permutasi yang tidak boleh berulang dapat dinotasikan:
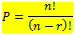
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








