Materi Matematika - Limit Fungsi Kelas 2

APSiswaNavbarV2

BelajarPintarV3

Menentukan Limit dengan Substitusi Langsung

Sobat pintar, dalam matematika limit merupakan nilai hampiran suatu variabel pada suatu bilangan real. Notasi :

di jabarkan sebagai "limit fungsi f(x) pada saat x mendekati a sama dengan L".

Teorema Limit Utama

Bila diketahui fungsi aljabar maka penyelesaiannya dicari sebagai berikut :

Nah sobat pintar, ada beberapa fungsi yang nilai limitnya dapat ditentukan dengan cara substitusi langsung seperti contoh berikut.

Contoh

Tentukan limit fungsi-fungsi berikut !

1.

2.

3.

Jawab :

3.

Bagaimana sobat pintar, apakah sudah paham ? Yuk lanjutkan lagi belajarnya...

Materi lebih lengkap ada di Apps Aku Pintar

Download GRATIS
Aplikasi Aku Pintar Sekarang Juga!

Materi lebih lengkap ada di Apps Aku Pintar

Download GRATIS
Aplikasi Aku Pintar Sekarang Juga!

Materi lebih lengkap ada di Apps Aku Pintar

Download GRATIS
Aplikasi Aku Pintar Sekarang Juga!

Materi lebih lengkap ada di Apps Aku Pintar

Download GRATIS
Aplikasi Aku Pintar Sekarang Juga!

Limit Tak Hingga dan Limit Fungsi di Tak Hingga

Limit (dibaca : tak hingga) digunakan untuk menyatakan nilai bilangan yang semakin besar. Jadi, 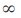bukan merupakan lambang bilangan dan tidak dapat dioperasikan secara aljabar sehingga tidak benar 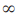- 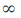= 0 atau = 1.

Untuk fungsi g(x) = ketika x menjadi sangat besar maka nilai 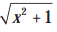pun bernilai semakin besar tanpa batas. Dalam lambang matematika, ditulis

Ingat :

Untuk menyelesaikan limit fungsi tak hingga sobat pintar dapat menggunakan teorema limit utama pada materi sebelumnya. Perhatikan contoh-contoh berikut :

Contoh

1.