Materi Matematika - Program Linear Kelas Persiapan SBMPTN - Belajar Pintar
BelajarPintarV3
Sistem Pertidaksamaan Linear Dua Variabel
Aapakah sobat pintar tau, apa itu program linear? Pemrograman linear ialah teknik optimasi yang melibatkan variabel-variabel linear. Dalam model pemrograman linear dikenal dua macam fungsi, yaitu fungsi objektif (objective function) dan fungsi kendala (constraint function) yang linear.
salah satu sub bab program linear adalah SPtLDV yaitu Sistem Pertidaksamaan Linear Dua Variabel. Apa itu SPtLDV? merupakan suatu pertidaksamaan dua variabel dengan pangkat setiap variabel satu.
Menentukan persamaan garis lurus Persamaan garis lurus yang sangat berkaitan dengan program linear ini adalah
1. Garis lurus yang melalui dua titik 
2. Garis lurus yang memotong sumbu X dititik (a,0) dan memotong sumbu Y di (0,b) mempunyai persamaan bx + ay = ab
Bagaimana nih sobat pintar, sudah faham belum dengan materi yang telah di sampaikan ? yuk kita diskusikan bersama sobat pintar lainnya
Metode Uji Titik Pojok
Tahukah sobat pintar? bahwa terdapat 2 cara untuk menentukan nilai optimum suatu fungsi objektif. Cara yang pertama adalah metode uji titik pojok, dan cara yang kedua adalah metode garis selidik. Dalam sub bab ini, kita akan bahas bagaimana sih cara menentukan nilai optimum suatu fungsi objektif dengan metode uji titik pojok.
Untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode uji titik pojok, lakukanlah langkah-langkah berikut.
a. Gambarlah daerah penyelesaian dari kendala-kendala dalam masalah program linear tersebut.
b. Tentukan titik-titik pojok dari daerah penyelesaian itu.
c. Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.
d. Bandingkan nilai-nilai fungsi objektif tersebut. Nilai terbesar berarti menunjukkan nilai maksimum dari fungsi f(x, y), sedangkan nilai terkecil berarti menunjukkan nilai minimum dari fungsi f(x, y).
untuk lebih mudahnya, coba sobat pintar lihat contoh soal berikut.
PT. Usaha Karya akan mencari keuntungan maksismum dalam produksi kompor dengan model matematika f(x, y)= 40.000x + 30.000y.
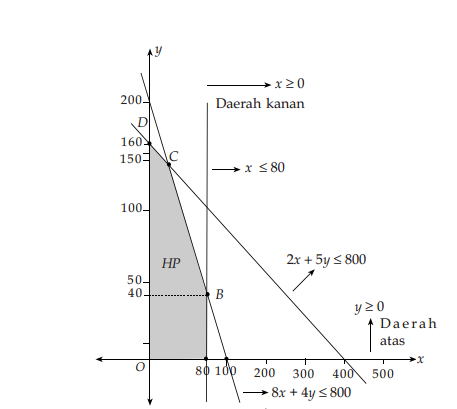
Perhatikan daerah penyelesaian dari grafik pada gambar di atas.
a. Titik-titik pojoknya adalah titik O, A, B, C, dan D.
• Titik O adalah titik pusat koordinat. Jadi, titik O(0,0).
• Titik A adalah titik potong antara garis x 80 dan sumbu-x. Jadi, titik A(80, 0).
• Titik B adalah titik potong antara garis x 80 dan garis 8x +4y=800.
Substitusi x = 80 ke persamaan
8x + 4y=800
8 .80 + 4y = 800
y = 40
Jadi, titik B(80, 40).
• Titik C adalah titik potong antara garis 8x + 4y = 800 dan 2x + 5y = 800.
Dari 8x + 4y = 800 didapat y 200 - 2x.
Substitusi nilai y ke persamaan 2x + 5y = 800
2x + 5(200 - 2x) = 800
2x + 1000 - 10x = 800
-8x = -200
x = 25
Substitusi x = 25 ke persamaan y = 200 - 2x
y = 200 - 2 · 25
y = 150
Jadi, titik C(25, 150).
• Titik D adalah titik potong antara garis 2x + 5y = 800 dan sumbu-y. Substitusi x = 0 ke persamaan 2x + 5y = 800
2 .0 + 5y = 800
5y = 800
y = 160
Jadi, titik D(0, 160).
b. Uji titik-titik pojok ke fungsi objektif f(x, y) = 40.000x + 30.000y, sehingga fungsi objektif ini maksimum.
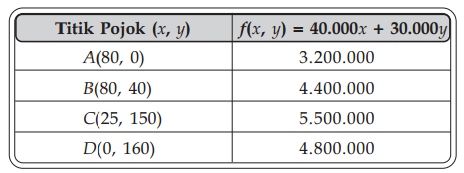
Dari tabel tersebut dapat diperoleh nilai maksimum fungsi objektif f(x, y) 40.000x + 30.000y adalah f(25, 150) = 5.500.000. Jadi, PT. Usaha Karya harus memproduksi 25 kompor dan 150 kompor sepeda untuk memperoleh keuntungan maksimum.
bagaimana sobat pintar? mudah bukan?
Materi Matematika SMA - Persiapan SBMPTN Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








