Materi Matematika - Bentuk Aljabar Kelas 7 - Belajar Pintar
BelajarPintarV3
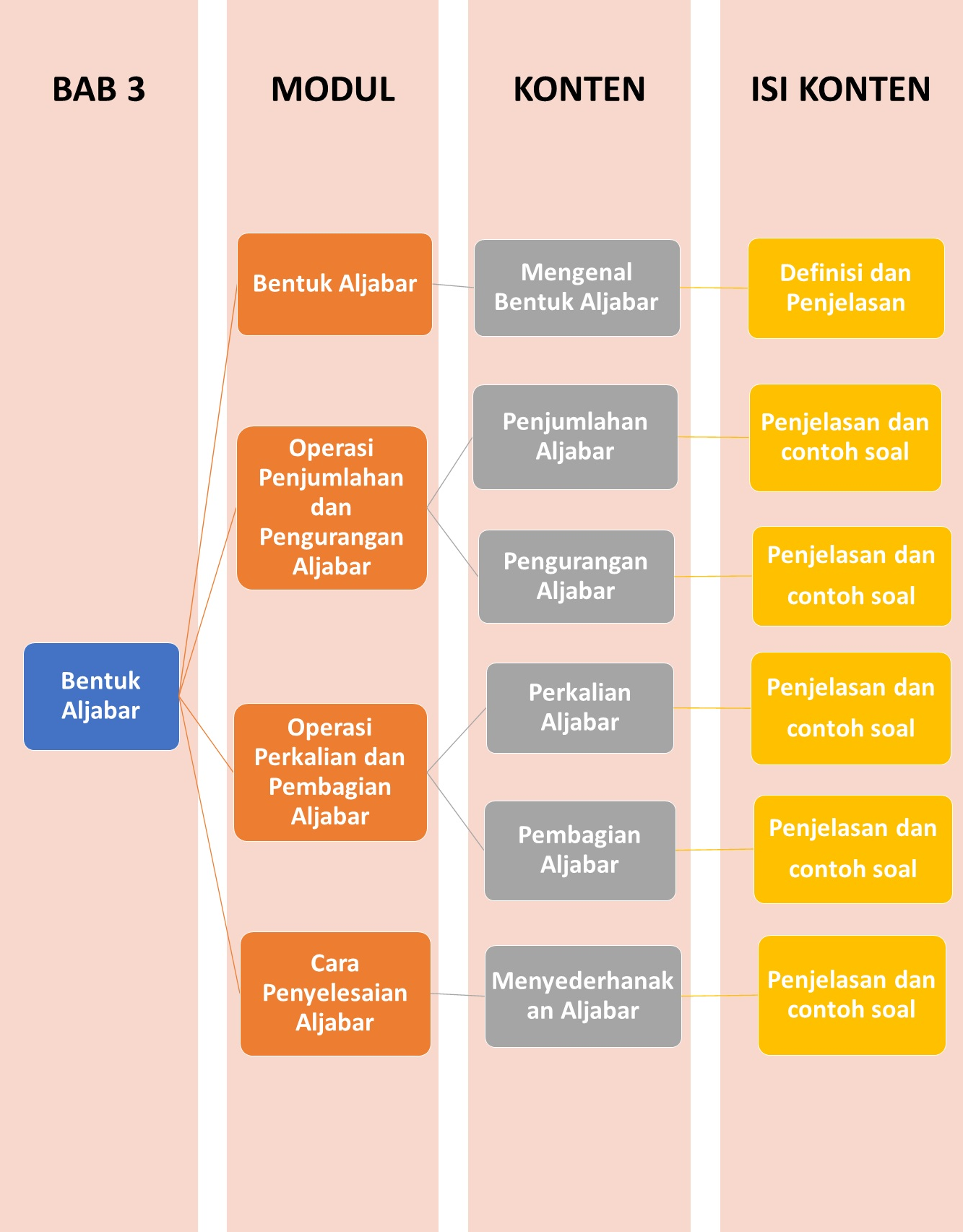
Peta Belajar Bersama
Halo Sobat Pintar, ini nih apa saja yang akan kita pelajari pada Bab ini..
Mengenal Bentuk Aljabar

Apasih yang dimaksud dengan bentuk aljabar? Yuk, Sobat Pintar perhatikan penjelasan dibawah ini.

Bu Halimah mempunyai sekeranjang apel. Bu Halimah ingin membagikan apel yang ia miliki tersebut kepada setiap orang yang ia temui. Setengah keranjang ditambah satu apel untuk orang pertama. Kemudian setengah dari sisanya ditambah satu, ia berikan kepada orang kedua yang ia temui. Selanjutnya, setengah dari sisanya ditambah satu, diberikan kepada orang ketiga yang ia temui. Sekarang, Bu Halimah hanya memiliki satu apel untuk ia makan sendiri. Tentukan banyak apel semula.
Kalian bisa memecahkan persoalan tersebut dengan cara memisalkan banyak apel mula-mula dalam keranjang dengan suatu simbol. Lalu kalian bisa membuat bentuk matematisnya untuk memecahkan permasalahan tersebut. Bentuk tersebut selanjutnya disebut dengan bentuk aljabar, dan operasi yang digunakan untuk memecahkan disebut operasi aljabar. Untuk lebih mengenal tentang bentuk dan operasi aljabar, mari mengikuti pembahasan berikut.
Contoh Soal :
Suatu ketika terjadi percakapan antara Pak Erik dan Pak Tohir. Mereka berdua baru saja membeli buku di suatu toko grosir.
Erik : “Pak Tohir, kelihatannya beli buku tulis banyak sekali.”
Tohir : “Iya, Pak. Ini pesanan dari sekolah saya. Saya beli dua kardus dan 3 buku. Pak Erik beli apa saja?”
Erik : “Saya hanya beli 5 buku Pak. Buku ini untuk anak saya yang kelas VII SMP.”
Dalam percakapan tersebut terlihat dua orang yang menyatakan banyak buku dengan satuan yang berbeda. Pak Tohir menyatakan jumlah buku dalam satuan kardus, sedangkan Pak Erik langsung menyebutkan banyak buku yang ia beli dalam satuan buku.
Penyelesaian :
Pada Tabel di atas, simbol x menyatakan banyak buku yang ada dalam kardus.
Simbol x tersebut bisa mewakili sebarang bilangan, yakni seperti berikut.
Jika x = 10, maka 2x + 3 = 2 x 10 + 3 = 20 + 3 = 23
Jika x = 15, maka 2x + 3 = 2 x 15 + 3 = 30 + 3 = 33
Jika x = 20, maka 2x + 3 = 2 x 20 + 3 = 40 + 3 = 43
Jika x = 40, maka 2x + 3 = 2 x 40 + 3 = 80 + 3 = 83
Jika x = 50, maka 2x + 3 = 2 x 50 + 3 = 100 + 3 = 103
Nilai pada bentuk aljabar di atas bergantung pada nilai x.
Pada soal diatas, kita mengenal beberapa bentuk aljabar, seperti : 2, x; 2x; 2x + 4, 2x + 3y + 7. Bentuk-bentuk yang dipisahkan oleh tanda penjumlahan disebut dengan suku. Berikut nama-nama bentuk aljabar berdasarkan banyaknya suku.
- 2, x, dan 2x disebut suku satu atau monomial
- 2x + 4 disebut suku dua atau binomial
- 2x + 3y + 7 disebut suku tiga atau trinomial
- Untuk bentuk aljabar yang tersusun atas lebih dari tiga suku dinamakan polinomial
Pada bentuk 2x + 4, bilangan 2 disebut koefisien, x disebut variabel, sedangkan 4 disebut dengan konstanta.
Contoh Soal :
Sederhanakan bentuk aljabar 4x + 9 - 5x – 2.
Penyelesaian :
Kelompokkan suku-suku sejenis
4x + 9 - 5x - 2 = 4x - 5x + 9 - 2
= (4 - 5)x + 7
= -1x + 7
-1x selanjutnya boleh hanya ditulis dengan -x, demikian juga 1x boleh hanya ditulis dengan x.
Dengan demikian, bentuk sederhana dari 4x + 9 - 5x - 2 adalah -x + 7.
Memahami Penjumlahan dan Pengurangan Bentuk Aljabar

Sobat Pintar, dalam materi sebelumnya kita telah mengenal bentuk aljabar, dalam materi kali ini kita akan mempelajari penjumlahan dan pengurangan bentuk aljabar
Dibawah ini merupakan contoh tabel penjumlahan dan pengurangan bentuk aljabar
Tabel Penjumlahan dan Pengurangan Bentuk Aljabar
Contoh Soal :
Pak Madhuri merupakan seorang pemborong beras yang sukses di desa Dempo Timur. Pak Madhuri mendapatkan pesanan dari Pedagang pasar Pasean dan Waru di hari yang bersamaan. Pedagang pasar Pasean memesan 15 karung beras, sedangkan pedagang pasar Waru memesan 20 karung beras. Beras yang sekarang tersedia di gudang Pak Madhuri hanya 17 karung beras saja. Misalkan x adalah massa tiap karung beras. Nyatakan dalam bentuk aljabar:
a. Total beras yang dipesan kepada Pak Madhuri.
b. Sisa beras yang ada di gudang Pak Madhuri jika memenuhi pesanan pedagang pasar Pasean saja.
c. Kekurangan beras yang dibutuhkan Pak Madhuri jika memenuhi pesanan pedagang pasar Waru saja.
Penyelesaian :
a. Total beras yang dipesan kepada Pak Madhuri adalah 15x + 20x atau 35x kilogram beras.
b. Jika Pak Madhuri memenuhi pesanan pedagang pasar Pasean saja, maka sisa beras adalah 2 karung beras atau 2x kilogram beras.
c. Kekurangan beras yang dibutuhkan Pak Madhuri untuk memenuhi pesanan Pedagang pasar Waru adalah 3 karung beras atau (-3x) kilogram beras. (tanda negatif menyatakan kekurangan)
Pada cerita pengantar tersebut terdapat operasi antara dua bentuk aljabar, yaitu:
1. Penjumlahan (15x) + (20x) = 35x
2. Pengurangan (17x) - (15x) = 2x
3. Pengurangan (17x) - (20x) = -3x
Bentuk 17x - 15x bisa juga ditulis penjumlahan dua bentuk aljabar (17x) - (15x)
Contoh Soal :
Tentukan penjumlahan 7a + 4b dengan 8a - 6b.
Penyelesaian :
(7a + 4b) + (8a - 6b) = 7a + 4b + 8a + (-6b)
= 7a + 8a + 4b + (-6b)
= 15a + (-2b)
= 15a - 2b
Contoh Soal :
Kurangkan 3x + 4y dengan 5x - 6y
Penyelesaian :
(3x + 4y) - (5x - 6y) = 3x + 4y - 5x + 6y
= 3x - 5x + 4y + 6y
= -2x + 10y
Perkalian Bentuk Aljabar

Bagaimana dengan penjelasan sebelumnya tentang penjumlahan dan pengurangan aljabar? Sekarang kita lanjut memahami tentang perkalian bentuk aljabar.
Secara umum hasil perkalian bentuk aljabar (x + a) × (x + b) mengikuti proses berikut.
Untuk lebih memahami perkalian bentuk aljabar Sobat Pintar dapat mempelajari contoh soal dibawah ini
Contoh Soal :
Pak Idris mempunyai kebun apel berbentuk persegi dan Pak Tohir mempunyai kebun jeruk berbentuk persegi panjang. Ukuran panjang kebun jeruk Pak Tohir 20 m lebih dari panjang sisi kebun apel Pak Idris. Sedangkan lebarnya, 15 m kurang dari panjang sisi kebun apel Pak Idris. Jika diketah i kedua luas kebun Pak Idris dan Pak Tohir adalah sama, maka tentukan luas kebun apel Pak Idris?
Penyelesaian :
Untuk memecahkan persoalan tersebut bisa dengan memisalkan panjang sisi kebun apel Pak Idris dengan suatu variabel, misal variabel x. Panjang kebun jeruk Pak Tohir 20 meter lebih panjang dari panjang sisi kebun apel bisa ditulis x + 20. Lebarnya 15 meter kurang dari panjang sisi kebun apel Pak Idris bisa ditulis x - 15. Seperti yang kita ketahui bahwa luas persegi panjang adalah panjang × lebar. Namun dalam permasalahan menentukan panjang sisi kebun tersebut, kita sedikit mengalami kesulitan karena yang dikalikan adalah bentuk aljabar. Dalam permasalah tersebut luas kebun Pak Tohir adalah hasil kali dari x + 20 dengan x - 15.
Luas kebun Pak Tohir dapat ditulis dalam bentuk aljabar
Luas = panjang x lebar
= (x + 20) x (x - 15)
= x2 - 15x + 20x - 300
= x2 + 5x - 300 satuan luas
Selain dengan cara tersebut, kita bisa menentukan luas kebun Pak Tohir dengan cara perkalian bersusun seperti berikut.
Jadi, luas kebun Pak Tohir adalah x2 + 5x - 300 satuan luas. Dari kedua cara tersebut, silakan menggunakan cara yang menurut kalian
paling mudah. Karena diketahui luas kebun apel Pak Idris sama dengan luas kebun jeruk PakTohir, maka didapat:
Luas kebun apel Pak Idris = Luas kebun jeruk pak Tohir
(x)2 = x2 + 5x - 300
x2 = x2 + 5x - 300
x2 - x2 = 5x - 300
0 = 5x - 300
5x = 300
x = 60
Jadi, luas kebun apel Pak Idris adalah (x)2 = (60)2 = 3.600 satuan luas.
Pembagian Bentuk Aljabar

Pada materi sebelumnya Sobat Pintar telah mempelajari perkalian dalam bentuk aljabar. Pada materi kali ini Sobat Pintar akan mempelajari pembagian dalam bentuk aljabar, mari kita simak materi dibawah ini
Untuk lebih memahami bagaimana pembagian dalam bentuk aljabar, mari Sobat Pintar mempelajari soal dibawah ini
Contoh Soal :
Jika informasi pada permasalahan tersebut diubah, yang diketahui adalah luas = x2 + 5x - 300 satuan luas, dan panjangnya = x + 20 satuan panjang, kalian diminta untuk menentuk bentuk aljabar dari lebarnya. Bagaimana langkah kalian untuk menentukan lebarnya?
Penyelesaian :
Seperti yang kita ketahui luas = panjang x lebar. Dapat kita tulis
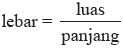
Lebar tanah Pak Tohir dapat ditentukan dengan membagi bentuk aljabar dari luas tanah dengan bentuk aljabar dari panjang.
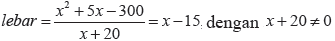
Jadi lebar tanah Pak Tohir adalah x-15
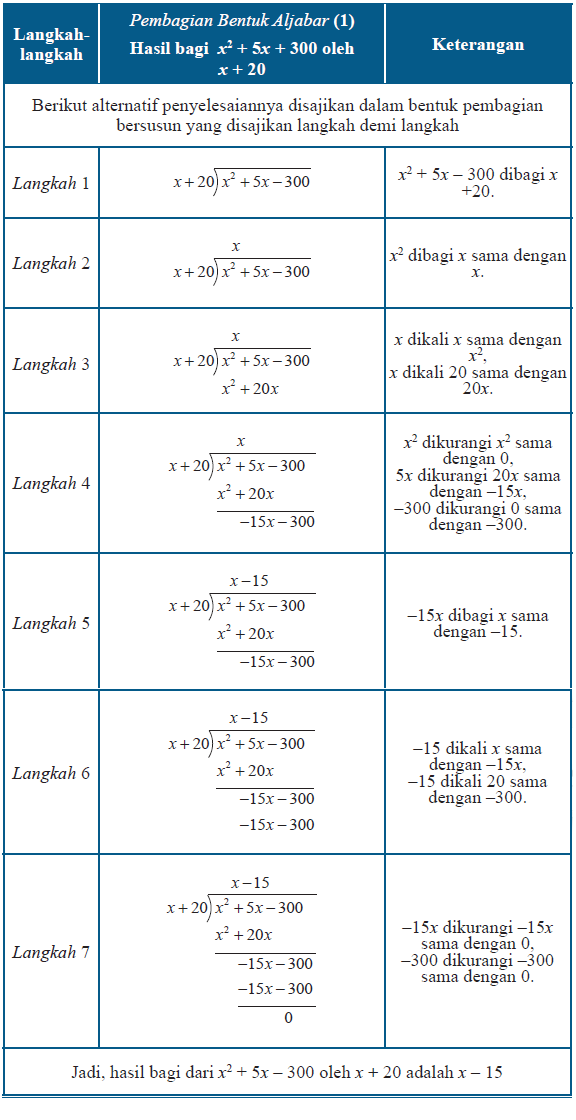
Berikut proses membagi bentuk aljabar disajikan dalam Tabel dibawah ini
Pembagian Bentuk Aljabar
Contoh Soal :
Tentukan hasil bagi dari (4x2 + 6x) oleh 2x
Penyelesaian :
Dengan cara membagi bentuk (4x2 + 6x) dengan 2x kalian bisa menemukan bentuk aljabar suku dua lainnya.
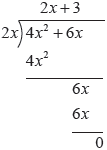
“Pada pembagian bentuk aljabar tidak selalu bersisa 0. Berikut contoh pembagian bentuk aljabar yang sisanya bukan 0”.
Contoh Soal :
Tentukan hasil bagi 2x2 + 3x - 4 oleh x + 3.
Penyelesaian :
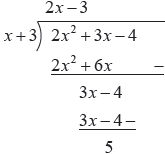
Jadi, hasil bagi 2x2 + 3x - 4 oleh x + 3. adalah 2x - 3 dengan sisa 5.
Cara Menyederhanakan Pecahan Bentuk Aljabar

Nah, Sobat Pintar. DI bagian ini kita akan bersama memelajari tentang menyederhanakan pecahan bentuk aljabar.
Dalam hal ini hasil baginya bisa disajikan dalam bentuk aljabar pecahan . Bentuk pecahan
bisa Sobat Pintar ubah menjadi bentuk yang lebih sederhana dengan cara membagi dua pembilang dan penyebutnya, menjadi
. Bentuk
dikatakan lebih sederhana karena mengandung bilangan-bilangan yang lebih sederhana (dekat dengan nol) dari bentuk sebelumnya. Namun, memiliki nilai yang sama dengan bentuk
. Selain itu, suatu bentuk aljabar dikatakan lebih sederhana jika mengandung operasi yang lebih sedikit.
Untuk lebih memahaminya mari kita simak contoh soal dibawah ini
Contoh Soal :
Sederhanakan pembagian bentuk aljabar dari 48x5y4z : 12x3y
Penyelesaian :
Cara untuk membagi bentuk aljabar dari 48x5y4z : 12x3y adalah sebagai berikut:
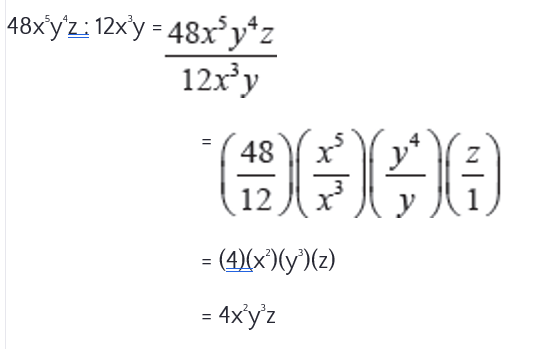
Cara menyelesaikan operasi pecahan bentuk aljabar sama halnya dengan menyelesaikan operasi bentuk bilangan bulat, yaitu sebagai berikut.
Materi Matematika SMP - 7 Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








