Materi Matematika - Bilangan Kelas 7 - Belajar Pintar
BelajarPintarV3
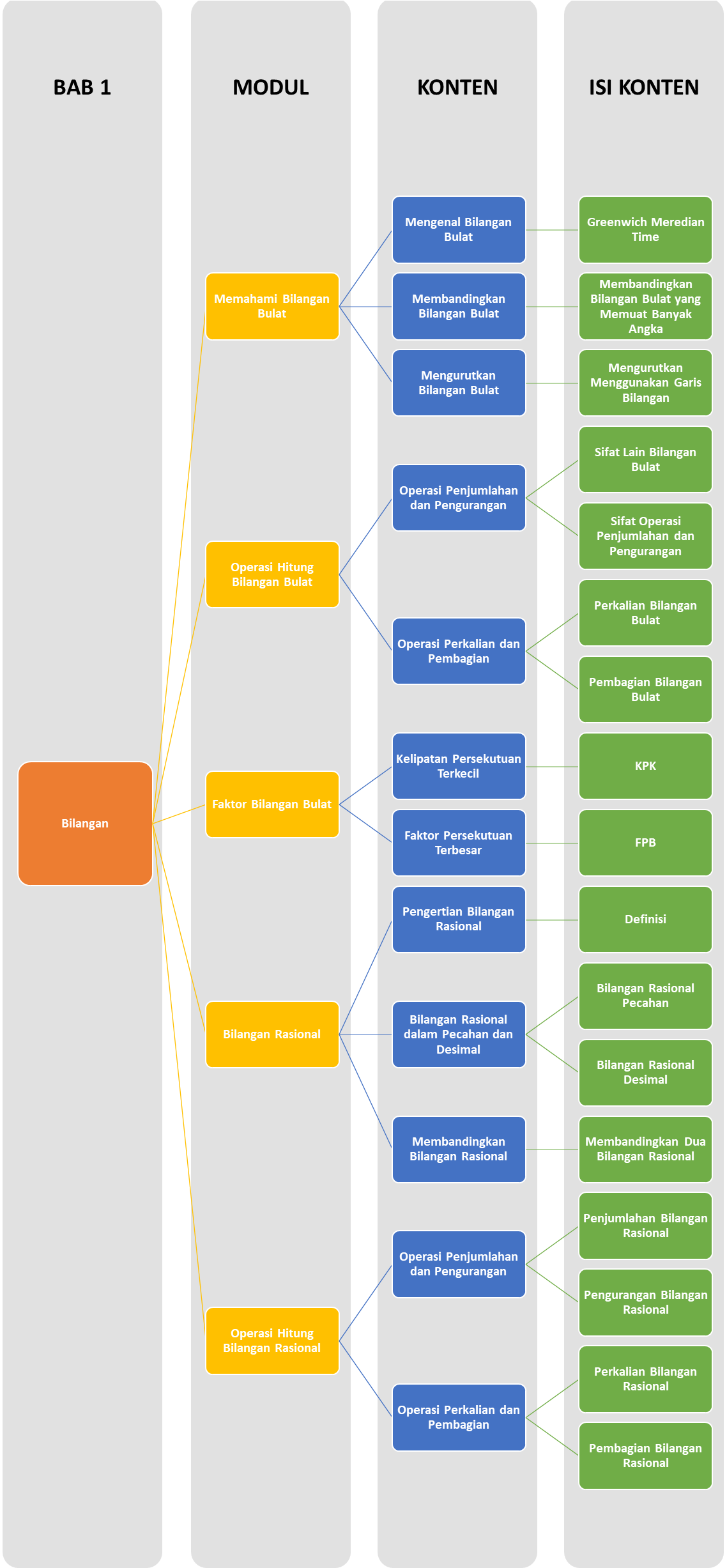
Peta Belajar Bersama
Halo Sobat Pintar, ini nih apa saja yang akan kita pelajari pada Bab ini..
Mengenal bilangan bulat

Sobat pintar, apakah kamu tahu bahwa pembagian zona waktu dunia berdasarkan GMT (Greenwich Meredian Time) menjadi standar acuan waktu dunia? Jika sekarang di Greenwich pukul 00.00 pukul berapakah di Papua?
Dengan penetapan kota Greenwich sebagai titik acuan atau titik nol waktu dunia, dapat kita lihat pengelompokan daerah dan urutannya. Pandang urutan bilangan yang ada pada Gambar 1.1. Berdasarkan GMT diperoleh sebagai berikut. Untuk menetapkan waktu Papua tambahkan waktu Greenwich sebesar 9 satuan, maka diperoleh waktu Papua adalah pukul 09.00 GMT.
Sifat-Sifat Operasi Penjumlahan dan Pengurangan pada Bilangan Bulat

Nah, Sobat Pintar. DI bagian ini, kita akan bersama mempelajari tentang mengenal sifat-sifat operasi penjumlahan dan pengurangan pada bilangan bulat.
Coba Sobat Pintar perhatikan beberapa soal dan jawaban dari operasi bilangan berikut:
Soal:
1. 800 + 70 = 870
2. 70 + 800 = 870
3. 650 + 30 = 680
4. 30 + 650 = 680
5. 780 – 120 = 660
6. 120 – 780 = -660
7. 580 + (-20) = 560
8. 580 – 20 = 560
Tentu kalian dengan mudah menentukan hasil dari soal-soal tersebut. Pada soal nomor 1 dan 2, posisi bilangan saling berkebalikan. Namun hasil dari kedua penjumlahan tersebut adalah sama, yaitu 870. Begitupun pada soal nomor 3 dan 4, hasilnya adalah sama, yaitu 680
Sifat 1: Komutatif
Secara umum, Jika a dan b adalah sebarang bilangan bulat, maka berlaku
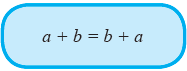
Apakah sifat komutatif juga berlaku pada operasi pengurangan? Ternyata tidak. Contohnya bisa kita lihat pada soal nomor 5 dan 6. Pada kedua soal tersebut, susunan bilangan yang dikurangi dan pengurangannya saling berkebalikan. Pada soal nomor 5, hasil pengurangannya adalah 660 . Sedangkan pada soal nomor 6, hasil pengurangannya adalah -660. Ternyata, jika kita cermati hasil keduanya tidak sama. Sehingga dapat kita simpulkan bahwa pada operasi pengurangan tidak berlaku sifat komutatif.
Sifat 2: Asosiatif
Selain sifat komutatif, pada penjumlahan bilangan bulat juga berlaku sifat asosiatif (pengelompokan). Secara umum, jika a, b, dan c adalah sebarang bilangan bulat, maka berlaku
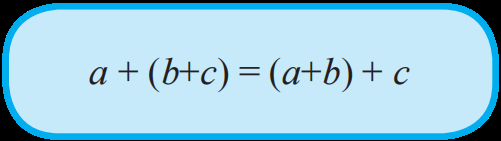
Perkalian Bilangan Bulat

Sobat Pintar, apakah ada hubungan antara operasi perkalian dengan operasi penjumlahan pada bilangan bulat?
Secara umum, untuk a elemen bilangan bulat positif dan b elemen bilangan bulat, a x b diartikan menjumlahkan b sebanyak a kali.
Pada operasi perkalian juga berlaku sifat komutatif, asosiatif, dan distributif. Untuk sebarang bilangan bulat a, b, dan, c berlaku:
1. Komutatif
a x b = b x a
2. Asosiatif
(a x b) x c = a x ( b x c)
3. Distributif
Perkalian terhadap penjumlahan
a x (b + c) = a x b + a x c
Perkalian terhadap pengurangan
a x (b - c) = a x b - a x c
Perkalian dua bilangan bulat tak nol
Keterangan:
Positif (+) : Sebarang bilangan bulat positif
Negatif (-) : Sebarang bilangan bulat negatif
Faktor Bilangan Bulat
Diketahui a dan b adalah bilangan bulat. a disebut faktor dari b jika ada n sedemikian sehingga b = a × n, dengan n adalah bilangan bulat.
Bilangan Prima
Bilangan prima adalah bilangan bulat positif yang hanya memiliki dua faktor, yaitu 1 dan bilangan itu sendiri. Misal p adalah bilangan prima maka faktor dari p hanya 1 dan p.
Kelipatan Persekutuan Terkecil

Apa yang Sobat Pintar tahu tentang kelipatan persekutuan?
Berikut penjelasan tentang kelipatan persekutuan.
Daftarlah sepuluh kelipatan bilangan berikut secara urut dari yang terkecil hingga terbesar. Kelipatan yang dimaksud adalah kelipatan bilangan bulat positif. Perhatikan Tabel berikut.
Dari Tabel diatas daftar bilangan-bilangan yang sama antara kelipatan 1 dan 2 adalah 2, 4, 6, 8, dan 10 Bilangan 2, 4, 6, 8, dan 10 disebut sebagai kelipatan persekutuan dari 1 dan 2. Sedangkan 2 disebut Kelipatan Persekutuan Terkecil (KPK) dari 1 dan 2.
Menentukan KPK dengan Faktorisasi Prima
Mari kita simak contoh soal dibawah ini
Contoh :
Tentukan KPK dari 90 dan 168.
Penyelesaian :
Langkah 1: menyatakan bilangan 90 dan 168 ke dalam bentuk faktorisasi prima. Untuk menentukannya bisa menggunakan bantuan pohon faktor, sebagai berikut.
90 = 2 x 32 x 5
168 = 23 x 3 x 7
Langkah 2: Mengalikan semua faktor-faktor pada masing-masing bilangan dengan ketentuan: Jika terdapat faktor prima yang sama pada kedua bilangan, maka dipilih yang pangkat tertinggi.
KPK dari 90 dan 168 adalah 23 × 32 × 5 × 7 = 2.520.
Menentukan KPK dengan Pembagian Bersusun
Mari kita simak contoh soal dibawah ini
Contoh :
Tentukan KPK dari 9, 15, dan 42.
Penyelesaian :
Langkah 1: Bagi ketiga bilangan tersebut secara bersusun hingga hasil bagi semua bilangan adalah 1, seperti berikut.
Keterangan:
Tanda panah merah berarti bilangan tersebut tidak terbagi habis oleh pembaginya.
Langkah 2: Kalikan semua pembagi
KPK dari 9, 15, dan 42 adalah 3 × 2 × 7 × 5 × 3 = 630
Pengertian Bilangan Rasional


Hai Sobat Pintar, mari kita perhatikan tabel di atas. Apakah kalian bisa melihat kaitan antara jenis bilangan yang satu dengan yang lain? Tampak bilangan asli termasuk dalam kategori bilangan cacah, dan bilangan cacah juga merupakan bagian dari bilangan bulat. Berikut adalah gambaran visualnya menggunakan diagram Venn.
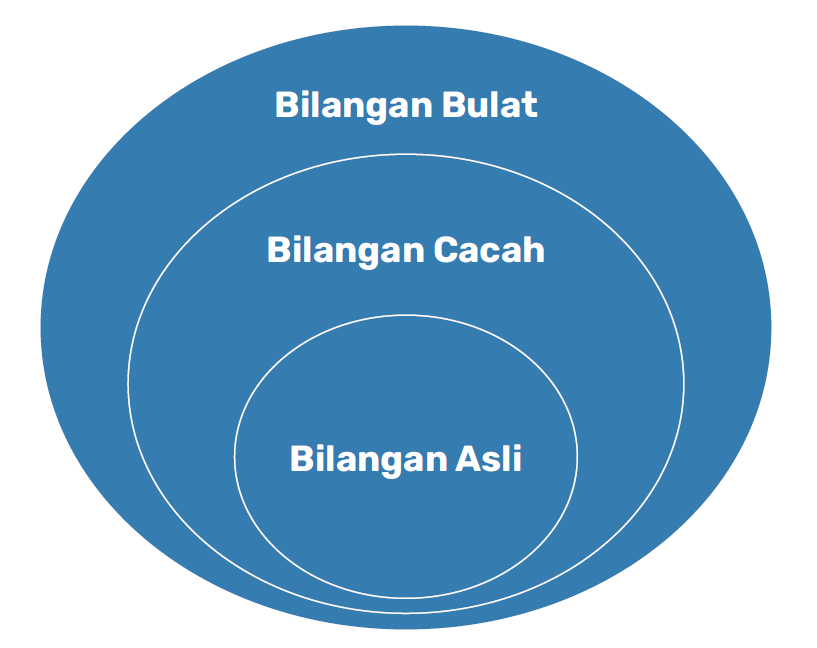
Dalam rangkaian dua bilangan bulat, terdapat sebuah bilangan lain yang tidak termasuk dalam kategori bilangan bulat. Bilangan itu disebut Bilangan Rasional. Sobat Pintar tau nggak apa definisi bilangan rasional? Bilangan rasional merujuk pada suatu bilangan yang dapat diwakili dalam bentuk pecahan biasa (a/b), dan jika dinyatakan dalam bentuk desimal, angkanya akan berhenti setelah sejumlah digit atau akan membentuk pola pengulangan.
Penjumlahan Bilangan Rasional

Untuk mengetahui penjumlahan bilangan pecahan dengan penyebut yang sama, sobat pintar dapat menyimak contoh soal dibawah ini
Contoh :
Tentukan hasil dari 1/3 +2/3
Penyelesesaian :
Penjumlahan 1/3 +2/3 dapat diilustrasikan menggunakan pita pecahan berikut.
Pita Pecahan
Perhatikan bahwa 1 objek utuh (keseluruhan) pada pita pecahan di atas tersusun dari 3 bagian yang sama Sepertiga
Jadi 1/3 +2/3= 3/3 = 1
3/3 bermakna 3 bagian dari 3 bagian yang sama dan berarti 1 objek utuh.
Untuk mengetahui penjumlahan bilangan pecahan dengan penyebut yang tidak sama, sobat pintar dapat menyimak contoh soal dibawah ini
Contoh :
Tentukan hasil dari 2/3 + 1/2
Penyelesesaian :
Penjumlahan 2/5+ 1/2 tidak dapat langsung dijumlahkan karena kedua pecahan tersebut memiliki bagian keseluruhan yang berbeda.
Pita Pecahan
Untuk menjumlahkan kedua pecahan tersebut kita harus mengubah menjadi pecahan ekuivalen yang penyebutnya sama. Dalam hal ini 2/5+ 1/2 dapat ditulis 4/10 + 5/10 , karena 4/10 ekuivalen dengan 2/5 , sedangkan 5/10 ekuivalen (senilai) dengan 1/2 . Perhatikan ilustrasi menggunakan pita pecahan berikut.
Pita Pecahan
Pita Pecahan
Perhatikan bahwa 1 objek utuh (keseluruhan) pada pita pecahan ini tersusun dari 10 bagian yang sama (sepersepuluhan).
Jadi 2/5 +1/2=4/10 + 5/10 = 9/10
9/10 bermakna 9 bagian yang sama dari 1 objek utuh (10 bagian yang sama).
Penjumlahan desimal dapat dikerjakan tanpa mengubah ke bentuk pecahan. Teknik bersusun ke bawah seperti pada penjumlahan bilangan bulat dapat digunakan. Jumlahkan sesuai dengan nilai tempatnya.
Contoh:
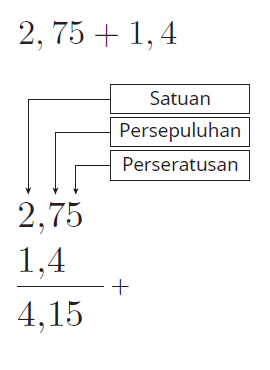
Perkalian Bilangan Rasional

Sobat Pintar, untuk mempelajari perkalian bilangan pecahan Mari kita simak contoh dibawah ini
Contoh :
Untuk meracik suatu ramuan obat, seorang apoteker menuang 1/2 liter cairan X setiap satu jam selama 5 jam. Berapa liter kandungan cairan X dalam ramuan obat tersebut?
Pembahasan :
Permasalahan tersebut bisa ditulis
![]()
Perkalian pecahan dalam garis bilangan
Dengan bantuan garis bilangan di atas, didapatkan ½ x 5 = 2 ½ atau 5/2
Jadi, banyak kandungan cairan X dalam ramuan obat tersebut adalah liter
Contoh :
Seorang apoteker ingin mengambil 1/2 dari cairan Y yang ada di dalam botol. Jika banyak cairan dalam botol adalah 4/5 bagian. Tentukan banyak cairan yang diambil oleh apoteker tersebut.
Pembahasan :
Bentuk permasalahan tersebut dapat diubah menjadi bagian dari cairan Y dalam botol. Jika dituliskan dalam perkalian
Untuk memahami perkalian dua bilangan pecahan agak sulit jika menggunakan garis bilangan. Kita bisa menggunakan pita bilangan untuk mengilustrasikan perkalian dua bilangan pecahan tersebut.
Perkalian menggunakan pita pecahan
Perhatikan daerah yang dikenai arsiran biru dan arsiran kuning. Daerah yang terkena arsiran biru dan kuning ada 4 bagian dari 10 bagian yang sama atau 4/10
Jadi 4/5 x 1/2 = 4/10
Untuk bentuk desimal, Sobat Pintar dapat menggunakan strategi mengubah bentuk desimal ke bentuk pecahan.

footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








