Materi Matematika - Sistem Persamaan Linear Dua Variabel Kelas 9 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, Ini nih ada Peta Belajar Bersama Matematika di BAB Kelima
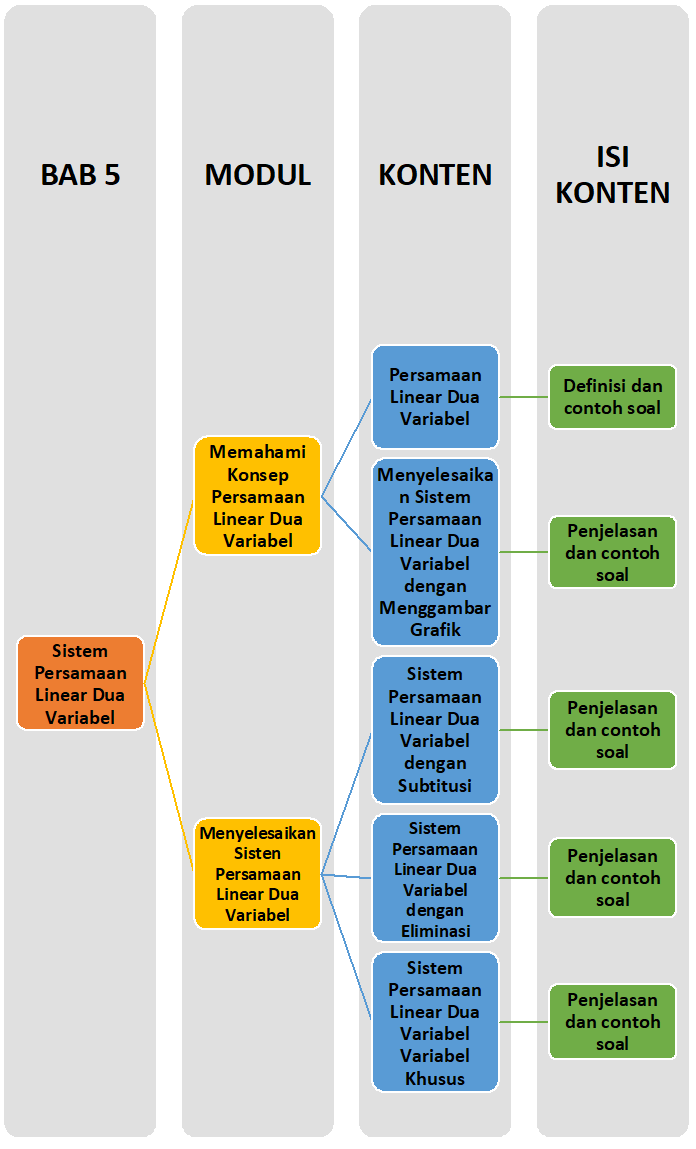
Yuk belajar bersama.....
Persamaan Linear Dua Variabel

Halo, Sobat Pintar, Kali ini akan membahas materi mengenai persamaan linear dua variabel.
Sistem persamaan adalah himpunan persamaan yang saling berhubungan. Variabel merupakan nilai yang dapat berubah-ubah. Persamaan linear adalah suatu persamaan yang memiliki variabel dengan pangkat tertingginya adalah 1 (satu). Sistem persamaan linear Dua Variabel (SPLDV) merupakan suatu sistem yang terdiri atas dua persamaan linier yang mempunyai dua variabel. Dalam sebuah Sistem Persamaan Linear Dua Variable (SPLDV) biasanya melibatkan dua persamaan dengan dua variabel.
Contoh SPLDV:
2x + 5y = 14
3a + 4b = 24
q + r = 3
Bentuk umum sistem persamaan linier dua variabel (SPLDV):
ax + by = c
Perhatikan contoh soal dibawah ini!
Contoh Soal :
Tentukan apakah pasangan berurutan berikut adalah salah satu selesaian dari persamaan yang diberikan.
Penyelesain :
a. y = 2x; (3, 6)
6 = 2(3)
6 = 6 (benar)
Jadi, (3, 6) adalah salah satu
selesaian dari y = 2x.
b. y = 4x - 3; (4, 12)
12 = 4(4) – 3
12 = 13 (salah)
Jadi, (4, 12) bukan
selesaian dari y = 4x - 3
Contoh Soal :
Perhatikan contoh soal dibawah ini!
Persamaan h = 2.000.000 + 150.000s menyatakan h (dalam rupiah) biaya yang dikeluarkan untuk studi lapangan sebanyak s siswa. Berapakah anyak siswa yang mengikuti studi lapangan jika biaya yang harus dikeluarkan adalah Rp7.700.000,00?
Penyelesaian :
Gunakan persamaan untuk menentukan nilai s dengan h = 7.700.000.
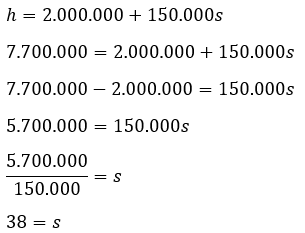
Jadi, banyak siswa yang ikut dalam studi wisata adalah 38 siswa. Kalian bisa menggunakan tabel dan grafik untuk menyajikan persamaan linear dua variabel.
Sistem Persamaan Linear Dua Variabel dengan Substitusi

Metode substitusi dilakukan dengan cara mensubstitusikan nilai salah satu variabel ke persamaan lainnya.
Langkah-langkah menyelesaikan SPLDV dengan metode substitusi :
1. Mengubah salah satu persamaan menjadi bentuk y = ax + b atau x = cy + d. TRIK!! Pilih persamaan yang paling mudah untuk diubah
2. Substitusi nilai x atau y yang diperoleh pada langkah pertama ke persamaan yang lainnya.
3. Selesaikan persamaan untuk mendapatkan nilai x atau y.
4. Substitusi nilai x atau y yang diperoleh pada langkah ketiga pada salah satu persamaan untuk mendapatkan nilai dari varabel yang belum diketahui.
5. Penyelesaiannya adalah (x, y).
Untuk lebih memahami tentang sistem persamaan linear dua vriabel dengan substitusi mari kita simak contoh soal dibawah ini
Contoh Soal :
Perhatikan contoh soal dibawah ini!
Selesaikan persamaan 2x + 3y = 8 dan 3x + y = 5 dengan menggunakan metode substitusi
Penyelesaian :
Langkah 1
3x + y = 5 ---> y = 5 - 3x
Langkah 2: substitusi y = 5 - 3x pada persamaan 2x + 3y = 8
2x + 3(5 - 3x)
Langkah 3: selesaikan persamaan sehingga diperoleh nilai x
2x + 3(5 - 3x) = 8
2x + 15 - 9x = 8
2x - 9x = 8 - 15
-7x = -7
x = 1
Langkah 4: substitusi nilai x = 1pada persamaan 2x + 3y = 8 (pilih salah satu, bebas, hasilnya akan sama).
2x + 3y = 8
2(1) + 3y = 8
2 + 3y = 8
3y = 8 - 2
3y = 6
y = 6/3
y = 2
Langkah 5: penyelesaiannya adalah (x, y)
Hasil yang diperoleh x = 1 dan y = 2. Penyelesaiannya adalah (1, 2)
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








