Materi Fisika - Getaran Harmonis Sederhana Kelas 10 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, ini nih ada Peta Belajar Bersama Fisika untuk bab sepuluh
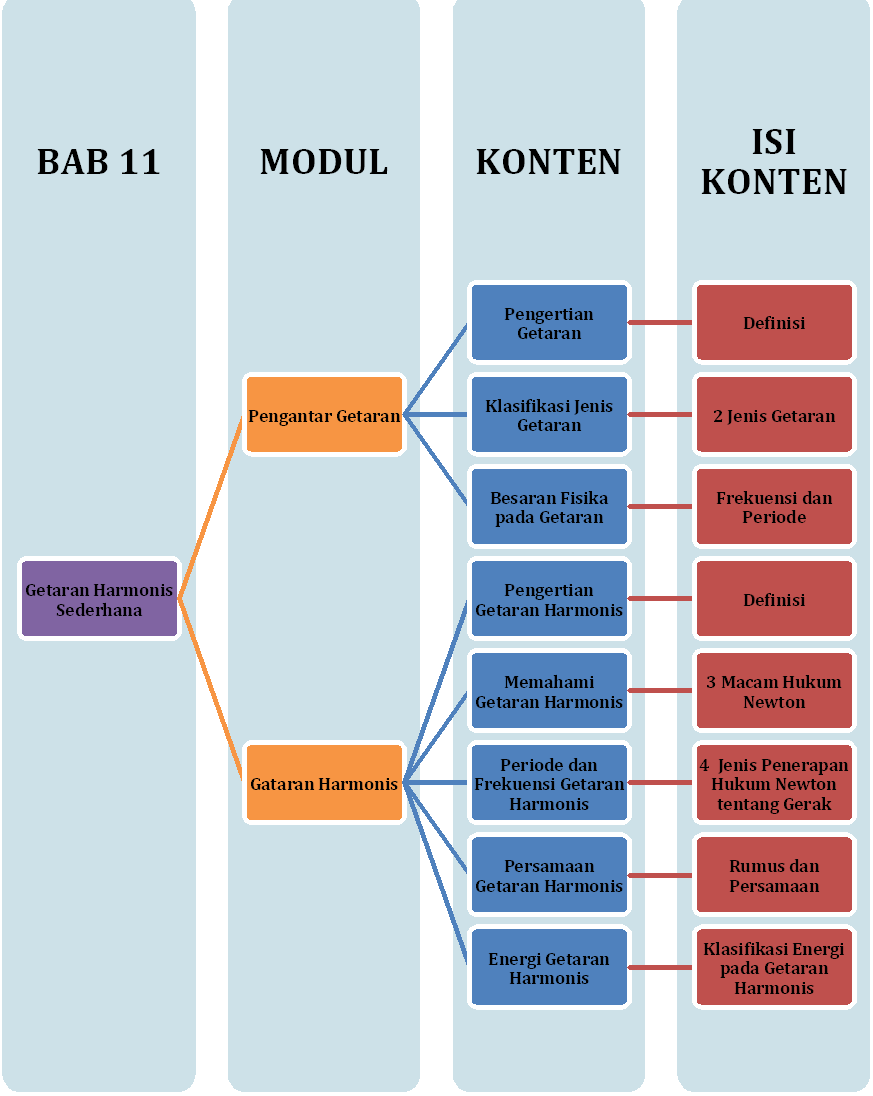
Yuk, mulai belajar bersama!
Pengertian Getaran


Sumber: https://vibrasiblog.blogspot.com/
Getaran adalah gerakan bolak-balik benda yang terjadi di sekitar titik keseimbangan. Kuat atau lemahnya getaran yang terjadi dipengaruhi oleh besar kecilnya energi yang menyebabkan getaran tersebut. Gerakan bolak balik ini terjadi secara teratur dan karena itu sering juga disebut gerak periodik. Satu getaran adalah satu kali bolak balik penuh dari benda tersebut.
Contoh sederhana dari getaran adalah cara kerja ayunan. Dalam fisika getaran berhubungan erat dengan gelombang. Gelombang adalah hasil dari getaran yang merambat baik melalui medium tertentu atau tanpa medium.
Pengertian Getaran Harmonis

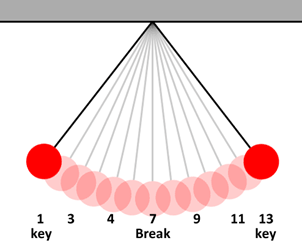
Sumber: http://poiemastudio.blogspot.com/
Gerak harmonik merupakan gerak sebuah benda dimana grafik posisi partikel sebagai fungsi waktu berupa sinus (dapat dinyatakan dalam bentuk sinus atau kosinus). Gerak semacam ini disebut gerak osilasi atau getaran harmonik. Contoh lain sistem yang melakukan getaran harmonik, antara lain, dawai pada alat musik, gelombang radio, arus listrik AC, dan denyut jantung. Galileo diduga telah mempergunakan denyut jantungnya untuk pengukuran waktu dalam pengamatan gerak.
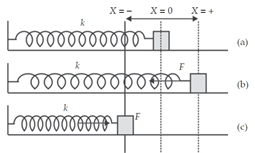
Sumber: https://fisikazone.com/
Gerak benda pada lantai licin dan terikat pada pegas untuk posisi normal (a), teregang (b), dan tertekan (c).
Materi Fisika SMA - 10 MIA Lainnya

Hakikat Fisika
5 Sub Bab Materi

Pengukuran
10 Sub Bab Materi

Vektor
4 Sub Bab Materi

Gerak Lurus
3 Sub Bab Materi

Gerak Parabola
2 Sub Bab Materi

Gerak Melingkar Beraturan (GMB)
2 Sub Bab Materi

Hukum Newton tentang Gerak
4 Sub Bab Materi

Hukum Newton tentang Gravitasi
5 Sub Bab Materi

Usaha dan Energi
3 Sub Bab Materi

Momentum dan Impuls
4 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







