Materi Fisika - Vektor Kelas 10 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama

Sobat, ini nih ada Peta Belajar Bersama Fisika untuk bab ketiga.
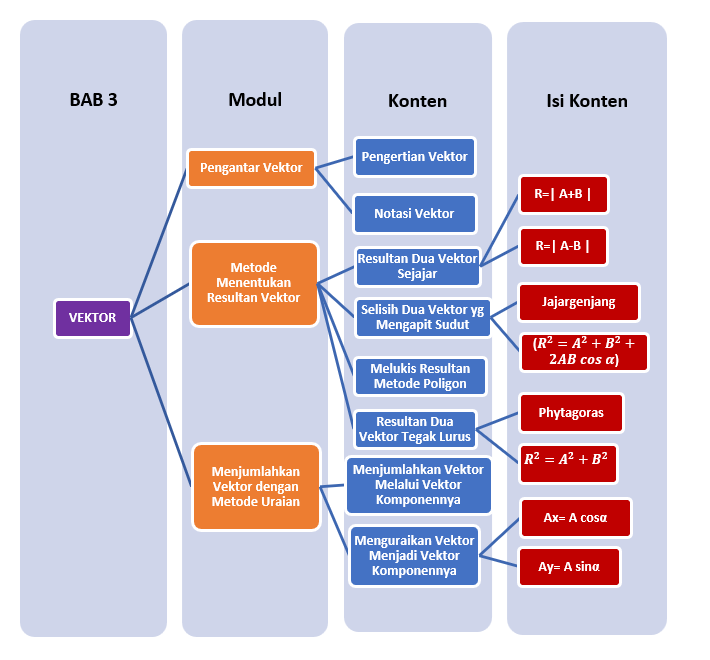
Yuk, mulai belajar bersama!
Pengertian Vektor


Sobat Pintar, perhatikan dua anak yang mendorong meja pada gambar tersebut. Apakah dua anak tersebut dapat mempermudah dalam mendorong meja? Tentu kalian sudah tahu bahwa arah gaya dorong sangat berpengaruh, karena keduanya memiliki arah berlawanan sehingga akan mempersulit meja untuk bergerak.
Nah, penyelesaian masalah-masalah ini perlu keterlibatan suatu besaran yaitu besaran vektor.
Besaran vektor adalah besaran yang memiliki nilai dan arah. Dalam ilmu Fisika, banyak besaran yang termasuk vektor, di antaranya perpindahan, gaya, kecepatan, percepatan, dan momentum.
Selain besaran vektor, ada juga besaran yang hanya memiliki nilai. Besaran seperti ini disebut besaran skalar. Besaran yang termasuk besaran skalar, di antaranya massa, waktu, kuat arus, usaha, energi, dan suhu. Sebuah vektor digambarkan oleh sebuah anak panah. Panjang anak panah mewakili besar atau nilai vektor, sedangkan arah anak panah mewakili arah vektor.
Resultan Dua Vektor Sejajar

Tahukah Sobat Pintar cara menentukan vektor resultan?
Misalnya, kalian bepergian mengelilingi kota Palu dengan mengendarai sepeda motor. Dua jam pertama, kalian bergerak lurus ke timur dan menempuh jarak sejauh 50 km. Setelah istirahat secukupnya, kalian kembali melanjutkan perjalanan lurus ke timur sejauh 30 km lagi.
Dilihat dari posisi asal, kalian telah berpindah sejauh sejauh 50 km + 30 km = 80 km ke timur. Dikatakan, resultan perpindahan kalian adalah 80 km ke timur. Secara grafis, perpindahan seperti diperlihatkan pada gambar berikut.

Sedikit berbeda dengan kasus tersebut, misalnya setelah menempuh jarak lurus 50 km ke timur, kalian kembali lagi ke barat sejauh 30 km. Relatif terhadap titik asal, perpindahan kalianmenjadi 50 km – 30 km = 20 km ke timur. Secara grafis, perpindahan diperlihatkan pada gambar berikut.
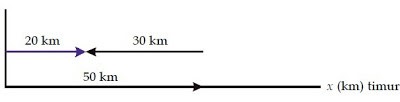
Dari kedua contoh, seperti yang diperlihatkan pada kedua gambar berikut, menjumlahkan dua buah vektor sejajar mirip dengan menjumlahkan aljabar biasa. Secara matematis, resultan dua buah vektor sejajar, yakni, sebagai berikut. Jika vektor A dan B searah, besar vektor resultan R, adalah
R = |A+B|
Dengan arah vektor R sama dengan arah vektor A dan B. Sebaliknya, jika kedua vektor tersebut berlawanan, besar resultannya adalah
R = |A-B|
Dengan arah vektor R sama dengan arah vektor yang terbesar.
Menguraikan Vektor Menjadi Vektor Komponennya

Sobat Pintar, dalam beberapa kasus, seringkali kalian menjumlahkan beberapa vektor yang lebih dari dua buah. Secara grafis, metode yang digunakan adalah metode poligon, seperti yang telah disinggung sebelumnya. Akan tetapi, bagaimanakah cara menentukan besar dan arah vektor resultannya?
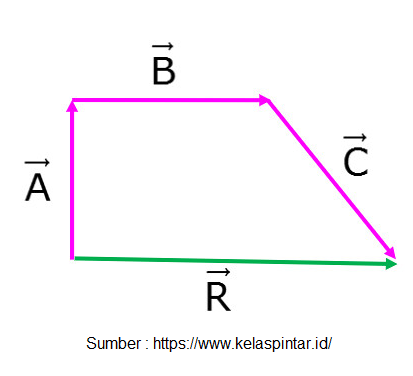
Salah satu metode yang digunakan adalah metode uraian, seperti yang akan dibahas pada sub bab berikut ini.
Sebuah vektor dapat diuraikan menjadi dua buah vektor yang saling tegak lurus. Vektor-vektor baru hasil uraian disebut vektor-vektor komponen.
Ketika sebuah vektor telah diuraikan menjadi vektor-vektor komponennya, vektor tersebut dianggap tidak ada karena telah diwakili oleh vektor-vektor komponennya. Sebagai contoh, ketika Sobat menguraikan sekarung beras 50 kg menjadi dua karung dengan masing-masing 20 kg dan 30 kg, apakah karung yang berisi 50 kg tetap ada?
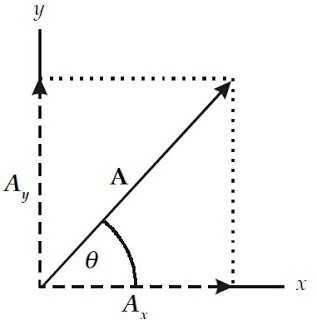
Gambar diatas memperlihatkan sebuah vektor A yang diuraikan menjadi dua buah vektor komponen, masing-masing berada pada sumbu-x dan sumbu-y. Ax adalah komponen vektor A pada sumbu-x dan Ay adalah komponen vektor A pada sumbu-y. Besar setiap komponen vektor A dapat ditulis sebagai berikut.
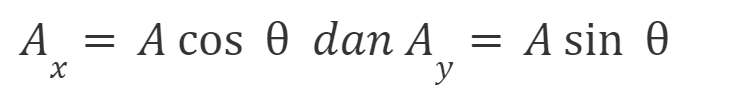
Sementara itu, dengan menggunakan Dalil Pythagoras diperoleh hubungan :
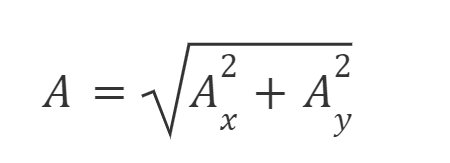
Selanjutnya, hubungan antara Ax dan Ay diberikan oleh :
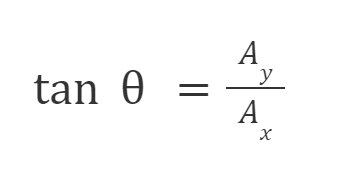
Materi Fisika SMA - 10 MIA Lainnya

Hakikat Fisika
5 Sub Bab Materi

Pengukuran
10 Sub Bab Materi

Gerak Lurus
3 Sub Bab Materi

Gerak Parabola
2 Sub Bab Materi

Gerak Melingkar Beraturan (GMB)
2 Sub Bab Materi

Hukum Newton tentang Gerak
4 Sub Bab Materi

Hukum Newton tentang Gravitasi
5 Sub Bab Materi

Usaha dan Energi
3 Sub Bab Materi

Momentum dan Impuls
4 Sub Bab Materi

Getaran Harmonis Sederhana
3 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







