Materi Matematika Wajib - Nilai Mutlak Kelas 10 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
Sebelum belajar Nilai Mutlak, coba perhatikan Peta Belajar Bersama dulu ya!
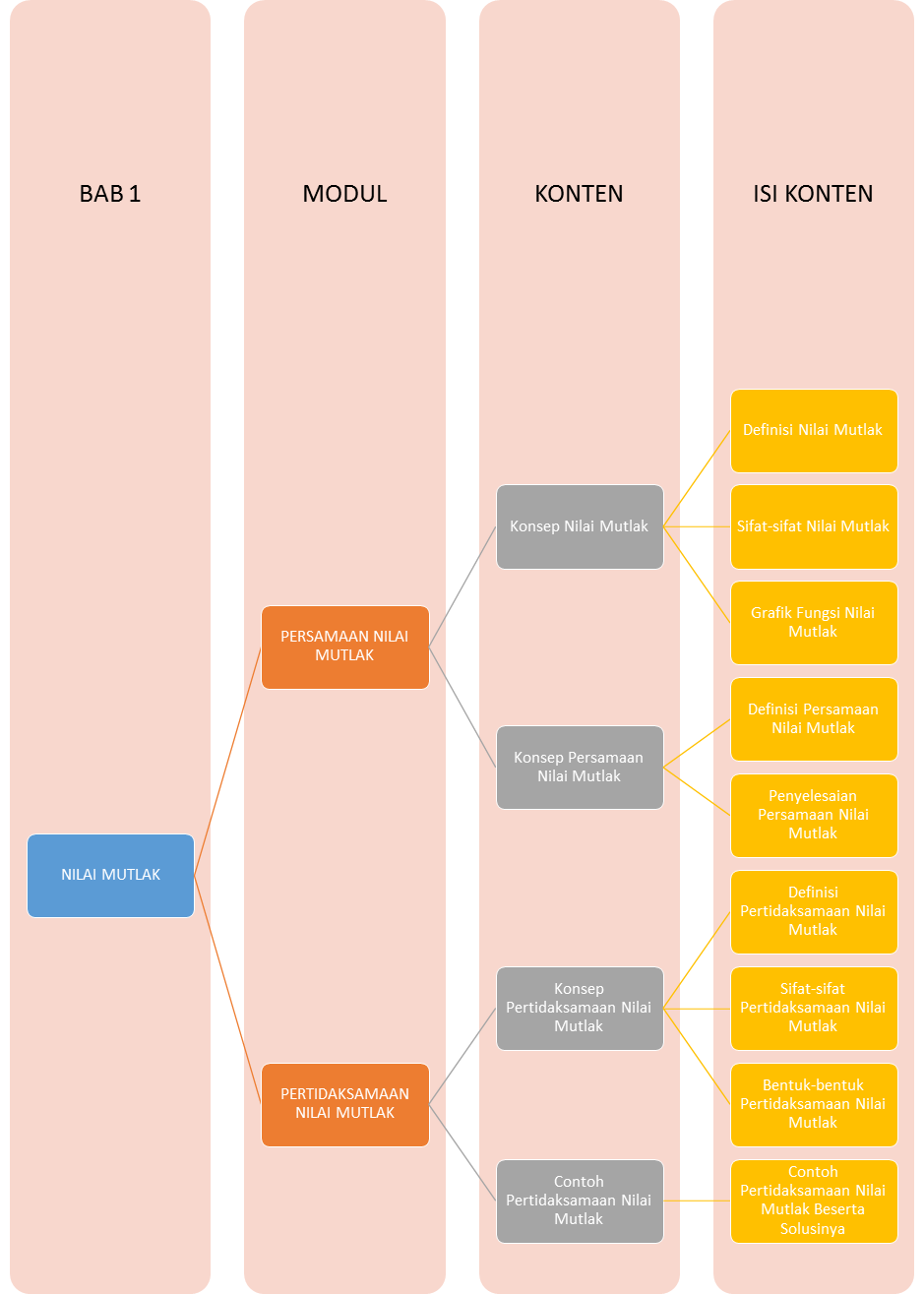
Yuk belajar bersama!
Konsep Nilai Mutlak


Sumber : Christtiny.blogspot.com
Halo, Sobat Pintar! Kalian pasti mengetahui tentang perpindahan dan jarak, bukan? Menurut kalian, apakah perpindahan dari satu tempat ke tempat lain bisa berupa bilangan negatif?
Kalau hasil perhitungannya negatif, bagaimana? Apakah perhitungan kita salah? Tentu tidak dong, sobat, karena suatu perpindahan yang dilakukan tidak memperhitungkan arah, tetapi hanya memperhitungkan banyak langkah selama kita berpindah.
Apakah logis jika banyaknya langkah yang kita lakukan itu bernilai negatif? Daripada makin bingung antara positif dan negatif, kita langsung aja yuk belajar tentang NILAI MUTLAK.
Nilai mutlak atau nilai absolut merupakan nilai dari sembarang bilangan yang tidak mungkin bernilai negatif, tetapi masih mungkin bernilai nol. secara matematis, nilai mutlak dapat didefinisikan:
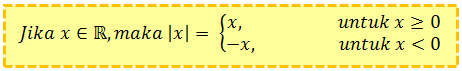
Jika terdapat nilai mutlak dalam bentuk aljabar, maka dapat dirumuskan sebagai berikut:

Sifat-Sifat Nilai Mutlak
Untuk x, y elemen bilangan real dengan y tidak sama dengan 0, berlaku sifat berikut:
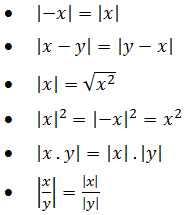
Grafik Fungsi Nilai Mutlak
Jika digambarkan dalam bentuk grafik, fungsi nilai mutlak akan membentuk garis lurus menyerupai huruf V pada interval tertentu.
Grafik fungsi nilai mutlak memiliki satu puncak dan simetris antara ruas kanan dan kirinya.
Grafik fungsi nilai mutlak selalu berada diatas sumbu x, karena sifat nilai mutlak yang selalu bernilai positif.
Langkah-langkah yang dilakukan dalam membuat grafik nilai mutlak yaitu
- Tentukan nilai x sehingga membuat y = 0
- Akan diperoleh titik koordinat (x,0) sebagai puncak grafik
- Selanjutnya gunakan titik bantu untuk menentukan titik lain yang dilalui grafik (dapat menggunakan bantuan tabel)
- Letakkan titik-titik koordinat yang diperoleh pada bidang koordinat cartesius
- Buatlah garis yang menghubungkan titik-titik pada bidang koordinat cartesius, sehingga diperoleh grafik suatu fungsi nilai mutlak
Konsep Pertidaksamaan Nilai Mutlak

Setelah membahas mengenai persamaan nilai mutlak, pernahkah kalian menemukan soal pertidaksamaan nilai mutlak?
Perhatikan tanda pertidaksamaannya ya karena dengan tanda berbeda maka beda pula penyelesaiannya!
Yuk kita pelajari bersama mengenai pertidaksamaan nilai mutlak.
Pertidaksamaan nilai mutlak adalah sebuah perbandingan nilai dua objek atau lebih yang selalu bernilai nonnegatif. Penyelesaian dari pertidaksamaan nilai mutlak dapat menggunakan grafik, definisi nilai mutlak atau menguadratkan kedua ruas
Berikut bentuk dari pertidaksamaan nilai mutlak beserta solusinya,
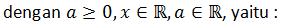

Jika fungsi dalam nilai mutlak berbentuk ax + b, maka bentuk pertidaksamaannya dapat diselesaikan sebagai berikut

Note: Next untuk membahas contoh soal ya, Sobat!
Materi Matematika Wajib SMA - 10 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








