Materi Matematika - Kesebangunan Kelas 7 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo Sobat Pintar, ini nih apa saja yang akan kita pelajari pada Bab ini..
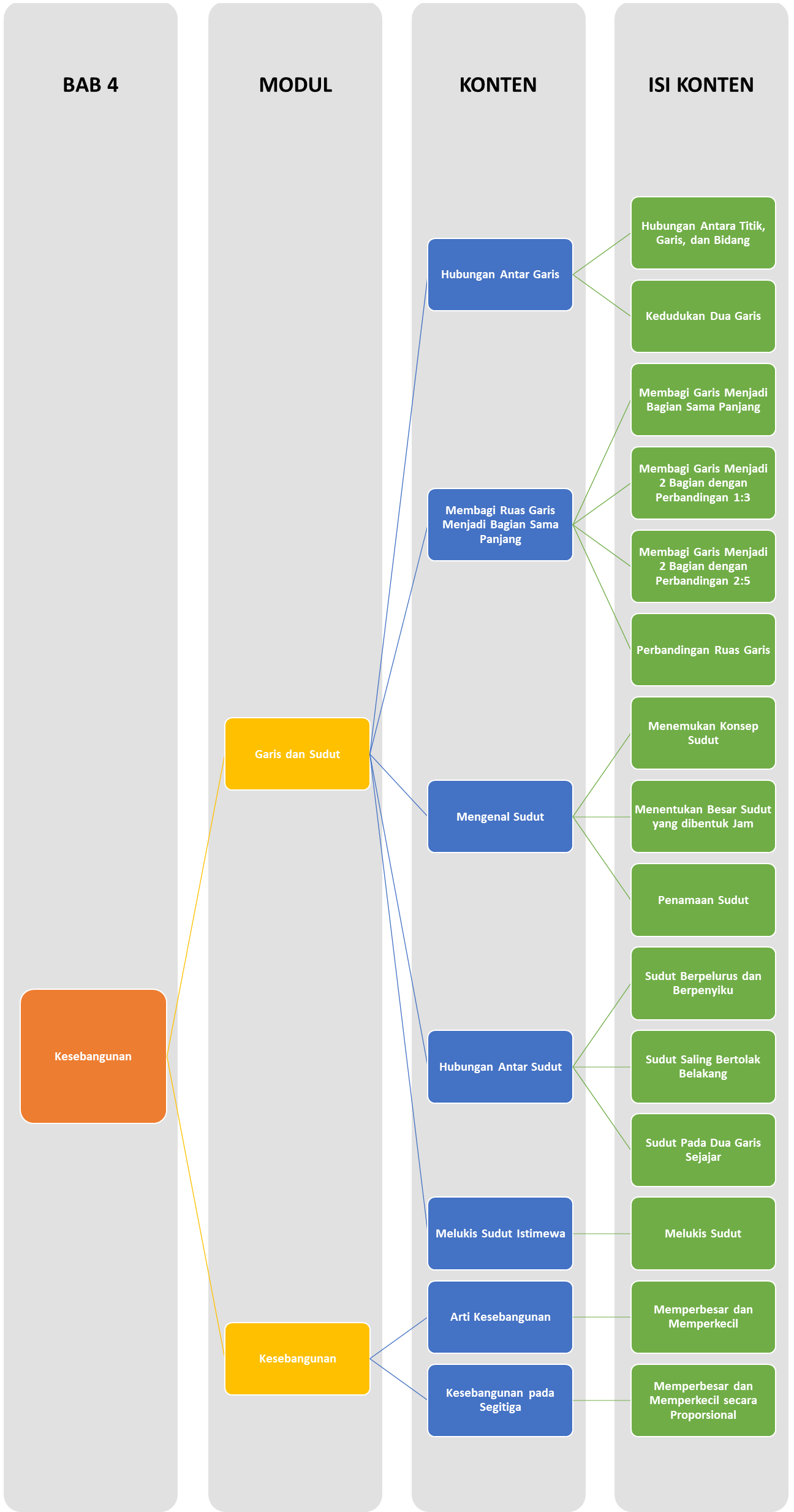
Hubungan Antara Titik, Garis, dan Bidang

Nah, Sobat Pintar. Di bagian ini kita akan bersama mempelajari tentang hubungan antar garis.
1. Hubungan Titik dan Garis
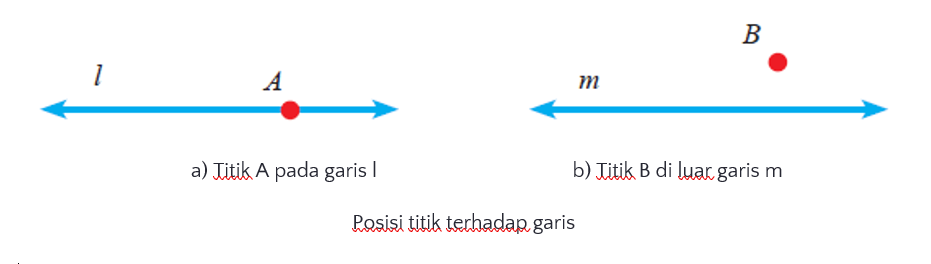
Hubungan antara titik dan garis dapat terjadi dalam dua kondisi. Pertama, titik terletak pada garis dan kedua, titik terletak di luar garis. Titik disebut terletak pada garis apabila titik tersebut ada pada garis, atau titik tersebut menjadi bagian dari garis. Pada Gambar dibawah ini berikut diperlihatkan hubungan titik dengan garis. Gambar dibawah ini memperlihatkan titik A yang terletak di garis l.
Sedangkan gambar b memperlihatkan letak titik B di luar garis. Titik di luar garis apabila titik tersebut tidak menjadi bagian dari garis.
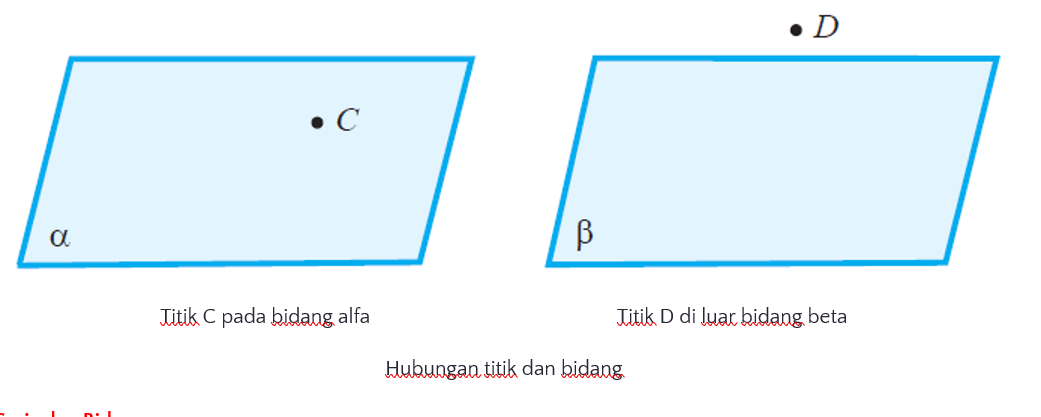
2. Hubungan Antara Titik dan Bidang
Keadaan di atas berlaku pula untuk hubungan titik dengan bidang. Titik terletak pada bidang atau titik tersebut menjadi bagian bidang. Perhatikan Gambar dibawah ini. Titik D tidak terletak pada bidang beta.
3. Hubungan Antara Garis dan Bidang
Hubungan antara garis dan bidang dapat diklasifikasikan menjadi tiga, yaitu:
1) garis terletak pada bidang,
2) garis tidak pada bidang, dan
3) garis menembus/memotong bidang.
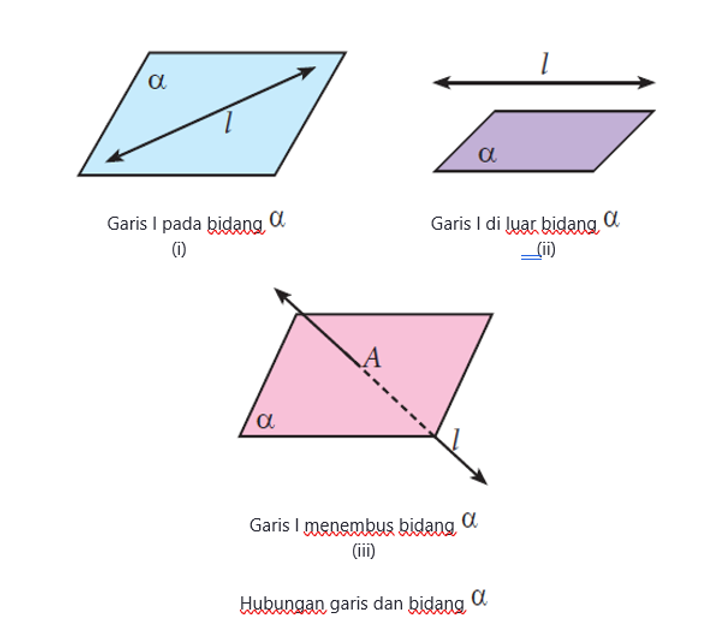
Garis terletak pada bidang apabila garis menjadi bagian dari bidang. Letak garis l pada bidang (gambar i) membagi titik-titik pada bidang menjadi dua bagian bidang.
Letak garis di luar bidang apabila garis tidak menjadi bagian bidang. Adapun garis menembus/memotong bidang apabila persekutuan antara garis dan bidang adalah sebuah titik. Berikut ilustrasi tiga kondisi/hubungan antara garis dengan bidang.
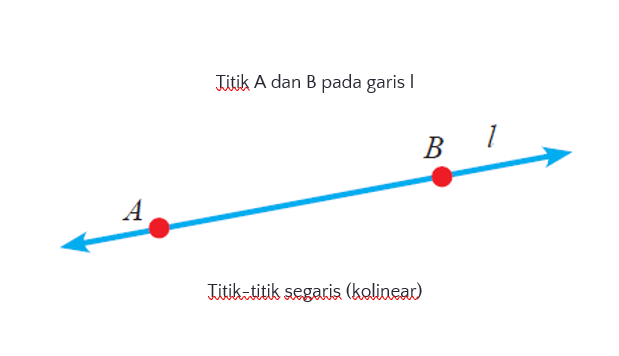
4. Titik-titik segaris
Dua titik atau lebih dikatakan segaris jika titik-titik tersebut terletak pada garis yang sama. Pada Gambar dibawah ini titik A dan titik B dikatakan segaris, karena sama sama terletak pada garis l. Sedangkan istilah titik-titik segaris bisa disebut kolinear
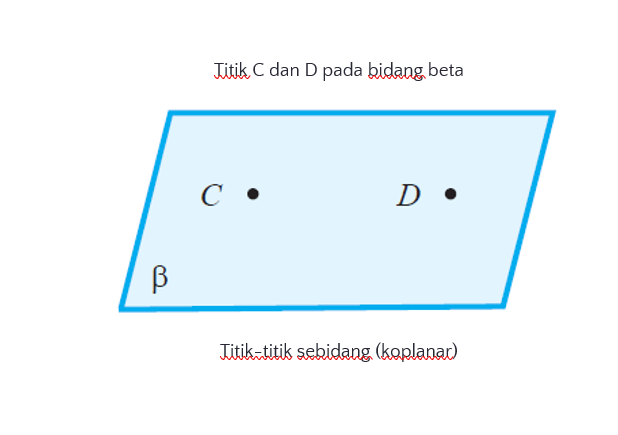
5. Titik-titik sebidang
Dua titik atau lebih dikatakan sebidang jika titik-titik tersebut terletak pada bidang yang sama. Pada Gambar dibawah ini titik C dan titik D dikatakan sebidang, karena sama-sama terletak pada bidang beta. Sedangkan istilah titik-titik sebidang bisa disebut koplanar.
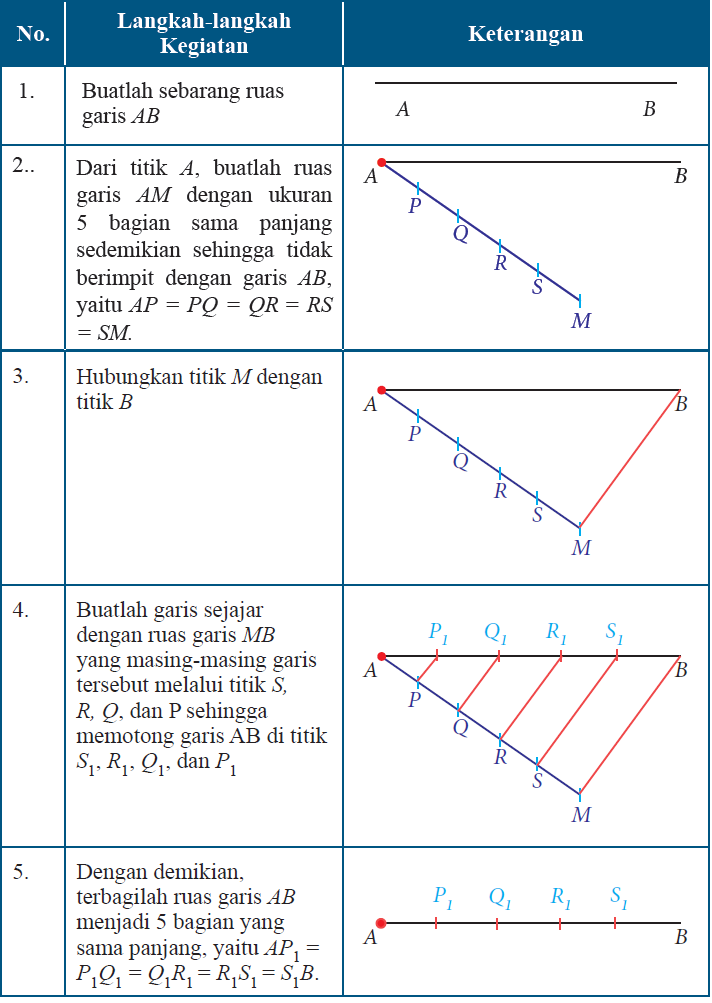
Membagi Garis Menjadi Beberapa Bagian Sama Panjang

Gunakan penggaris untuk membagi sebuah ruas garis menjadi beberapa bagian sama panjang, kemudian ikutilah langkah-langkah pada Tabel berikut ini.
Tabel Membagi Garis AB Menjadi 5 Bagian Sama Panjang
Menemukan Konsep Sudut

Secara matematis, hubungan sinar garis dan titik sudut diilustrasikan sebagai berikut.
Gambar Sudut yang terbentuk oleh dua sinar garis
Suatu sudut terbentuk dari perpotongan dua sinar garis yang berpotongan tepat di satu titik, sehingga titik potongnya disebut dengan titik sudut.
Nama suatu sudut dapat berupa simbol alfa, beta, dll, atau berdasarkan titik titik yang melalui garis yang berpotongan tersebut. Biasanya, satuan sudut dinyatakan dalam dua jenis, yaitu derajat ("o") dan radian (rad). Sudut APB bisa juga disebut Sudut P, dan besar sudut P dilambangkan dengan m sudut P.
Keterangan: Besar sudut satu putaran penuh adalah 360o
Sudut Berpelurus dan Sudut Berpenyiku

1. Sudut berpelurus
Sudut berpelurus adalah sudut yang apabila dijumlahkan keduanya bernilai 180o.
Berpelurus diambil dari kata dasar lurus yang dibentuk oleh sebuah garis lurus adalah 180o. Dua sudut yang disebut saling berpelurus adalah apabila jumlah besar kedua sudut tersebut adalah 180o. Sudut yang satu disebut pelurus dari sudut yang lain.
Dengan demikian misalkan Sudut ABD dan Sudut CBD saling berpelurus, maka Sudut ABD + Sudut CBD = 180o. Untuk lebih jelasnya perhatikan gambar dibawah ini
2. Sudut berpenyiku
Sudut berpenyiku adalah sudut yang apabila dijumlahkan keduanya bernilai 90o.
Sesuai dengan judul berpenyiku dengan kata dasar siku atau siku-siku maka besar sudutnya adalah 90o. Apabila dua sudut yang letaknya saling bersebelahan membentuk sudut siku-siku atau jumlah besar sudutnya 90o maka sudut-sudut tersebut dapat dikatakan saling berpenyiku atau disebut juga komplemen. Sudut yang satu disebut penyiku dari sudut yang lain.
Dengan demikian misalkan Sudut ADB dan Sudut BDC saling berpenyiku, maka Sudut ADB + Sudut BDC merupakan penyiku dari Sudut ABC. Perhatikan gambar dibawah ini
Melukis Sudut

Pada materi kali ini Sobat Pintar akan mempelajari tentang melukis sudut-sudut istimewa (90o, 60o, 45o, dan 30o). Agar kalian dapat melukis sudut-sudut istimewa tersebut, coba sekarang sediakan suatu alat berupa jangka dan penggaris.
a. Melukis Sudut 90o
Untuk melukis sudut 90o, ikutilah langkah-langkah pada tabel berikut ini berikut ini:
Tabel Melukis Sudut 90o
b. Melukis Sudut 60o
Untuk melukis sudut 60o, ikutilah langkah-langkah pada tabel berikut ini berikut ini:
Tabel Melukis Sudut 60o
c. Membagi Sudut Menjadi Dua Sama Besar
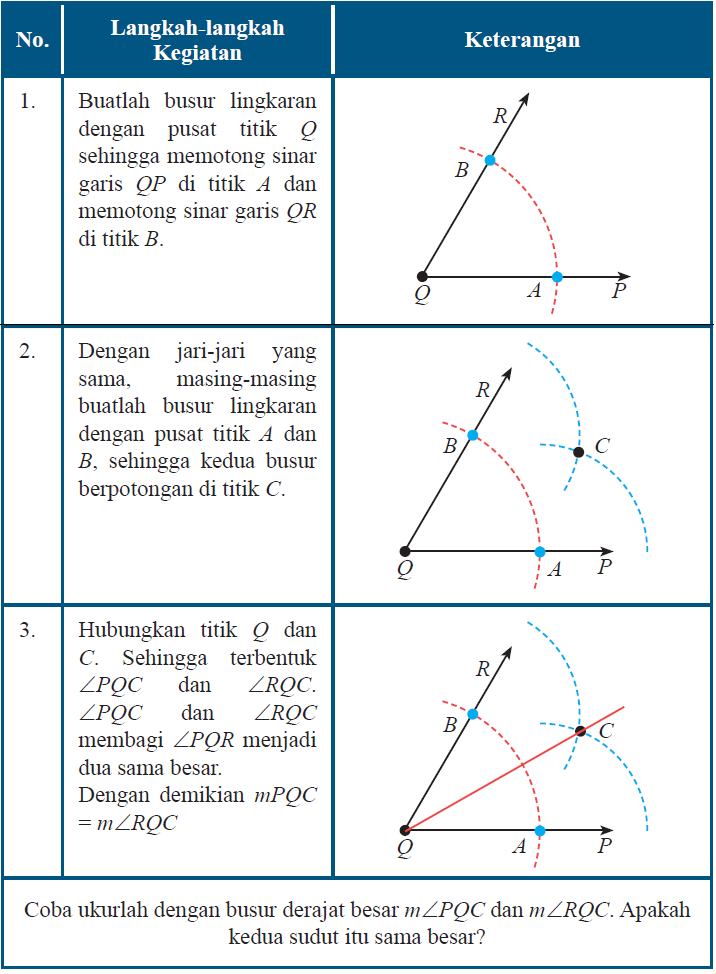
Misalkan kita akan membagi Sudut PQR seperti pada Gambar berikut menjadi dua sama besar.
Ikutilah langkah-langkah pada tabel berikut ini :
Tabel Membagi sudut menjadi dua sama besar
Arti Kesebangunan


Hai Sobat Pintar, perhatikanlah pas foto pada Gambar di atas yang dicetak dengan ukuran yang berbeda-beda. Meskipun memiliki ukuran yang berbeda, foto yang tercetak tetap memiliki bentuk yang sama. Dalam matematika, istilah yang digunakan untuk ini adalah "sebangun". Benda yang sebangun dapat memiliki ukuran yang berbeda, namun bentuknya tetap sama.
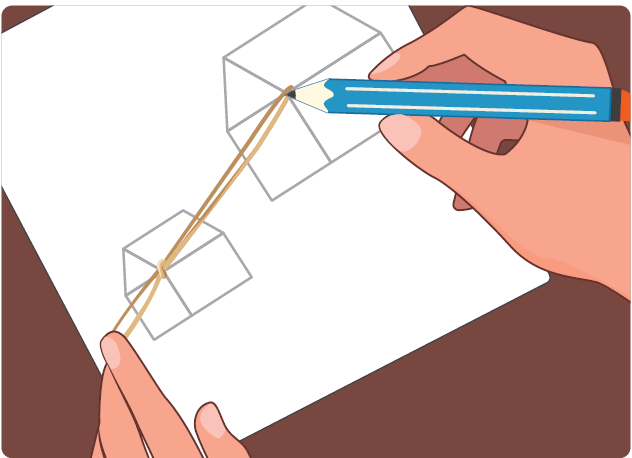
Dalam konteks elektronik, kita dapat memperbesar dan memperkecil dengan menggunakan fitur zoom in dan zoom out. Sobat bisa mencoba melakukan perbesaran secara sederhana dengan langkah-langkah berikut:
- Kaitkan dua buah karet gelang dengan simpul.
- Dengan salah satu jari, tekan salah satu ujung karet pada sebuah titik (jaga sehingga bagian ini tidak bergeser selama kegiatan). Sebaiknya gunakan tangan yang berbeda dengan tangan yang akan memegang pensil.
- Kaitkan pensil pada ujung yang lain. Tariklah karet sehingga simpul karet bergerak menelusuri gambar.

Materi Matematika SMP - 7 Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








