Materi Matematika IPA - Matriks mat Kelas Umum - Belajar Pintar
BelajarPintarV3
Apa itu matriks?
Pengertian matriks adalah kumpulan bilangan (atau unsur) yang disusun menurut baris dan kolom tertentu. Bilangan-bilangan yang disusun tersebut dinamakan eleme-elemen atau komponen-komponen matriks. Nama sebuah matriks biasanya dinyatakan dengan huruf kapital. Dalam sebuah matriks ada istilah ordo. Yang dimaksud dengan ordo atau ukuran matriks adalah banyaknya baris x banyak kolom dalam sebuah matriks.
Contoh
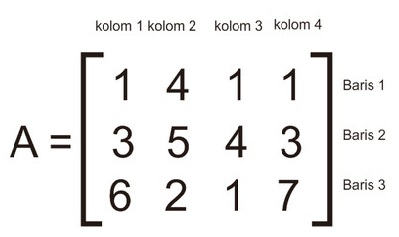
Matriks A di atas terdiri dari 3 baris dan 4 kolom. Sobat bisa mengatakan matriks A berordo 3 x 4 atau bisa sobat hitung tulis A(3×4).
Oke sobat pintar kita lanjut ke materi berikutnya.
Penjumlahan dan Pengurangan Matriks
Setelah memasuki bab matriks, mari kita bahas operasi hitung matriks dimulai dari penjumlahan dan pengurangan matriks.
Coba sobat pintar Perhatikan bahwa kedua matriks yang dijumlahkan memiliki ordo yang sama. Hasil matriks yang diperoleh adalah matriks yang berordo sama, diperoleh dengan cara menjumlahkan elemen-elemen yang seletak.
Bagaimana dengan pengurangan matriks? Pengurangan matriks juga dapat dilakukan jika ordo matriks yang akan dikurangkan sama. Hasil pengurangan matriks ini merupakan matriks yang berordo sama, diperoleh dengan cara mengurangkan elemen-elemen yang seletak.
Jika sobat pintar masih binung, coba sobat pintar perhatikan contoh soal berikut :
Diketahui dua buah matriks sebagai berikut :
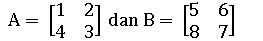
Tentukan nilai dari 3A - 2B.
Pembahasan:
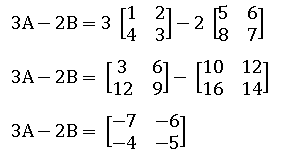
Bagaimana sobat pintar, mudah bukan?
Determinan
Suatu matriks persegi selalu dapat dikaitkan dengan suatu bilangan yang disebut determinan. Determinan dari matriks persegi A dinotasikan dengan |A|.
Untuk matriks A berordo 2 x 2, determinan matriks A didefinisikan sebagai berikut.
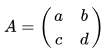
maka Determinan |A| adalah:
|A| = ad - bc
Adapun untuk matriks B berordo 3x3, determinan matriks B ini didefinisikan sebagai berikut menggunakan kaidah Sarrus.
Jika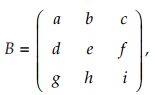 maka determinan matriks B adalah
maka determinan matriks B adalah
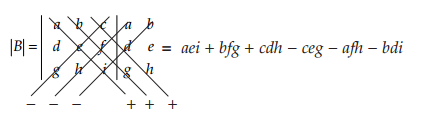
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








