Statistika

Mean data tunggal

Pengertian dari Mean sendiri adalah nilai rata – rata hitung dan didalam Rumus Mean (Rumus Rataan Hitung) bisa dilakukan dengan cara membagi Jumlah Nilai data dg banyaknya data tersebut. Lalu Rumus Statistika Mencari Rataan Hitung tersebut memiliki tiga rumus yang terbagi antara lain :

1. Mean Data Tunggal

 

2. Mean data distribusi frekuensi

3. Mean data berkelompok

agar sobat pintar lebih memahami rumus-rumus di atas, perhatikan contoh di bawah ini kemudian kalian dapat mencoba beberapa latihannya

Contoh Soal :

1. Dari data tunggal berikut :

5, 6, 6, 6, 7, 7, 8, 9, 10

tentukanlah mean (rata-rata)!

Jawab :

Rata-rata hitung (mean) = jumlah semua nilai / banyak nilai

Rata-rata hitung (mean) = (5+3×6+2×7+8+9+10)/9

Rata-rata hitung (mean) = 64 / 9

Rata-rata hitung (mean) = 7,1

2. Data di bawah ini menunjukkan nilai ulangan matematika dari sekelompok siswa, tentukanlah nilai rata-rata (mean)!

Nilai	4	5	6	7	8	9
Frekuensi	3	4	7	6	3	2

Jawab :

Mean = (3×4+4×5+7×6+6×7+3×8+2×9)/(3+4+7+6+3+2)

Mean = 158 / 25 = 6,3

Median (Nilai tengah)

Sobat pintar, di modul sebelumnya kita telah mempelajari tentang rataan hitung atau mean. Sekarang kita lanjut ke materi tentang Median (nilai tengah).

Median adalah suatu nilai tengah yang telah diurutkan. Median dilambangkan Me.

1. Untuk menentukan nilai Median data tunggal dapat dilakukan dengan cara:

a) mengurutkan data kemudian dicari nilai tengah,

b) jika banyaknya data besar, setelah data diurutkan, digunakan rumus:

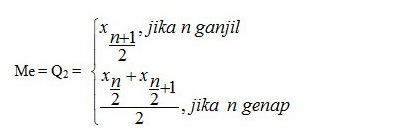
Contoh:

Tentukan median dari data: 2, 5, 4, 5, 6, 7, 5, 9, 8, 4, 6, 7, 8

Jawab:

Data diurutkan menjadi: 2, 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 8, 9

Median = data ke-(13 + 1)/2

= data ke-7

Jadi mediannya = 6

2. Median data berkelompok

Jika data yang tersedia merupakan data kelompok, artinya data itu dikelompokkan ke dalam interval-interval kelas yang sama panjang.

Untuk mengetahui nilai mediannya dapat ditentukan dengan rumus berikut ini.

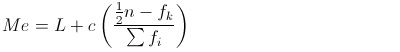
Keterangan:

Kelas median adalah kelas yang terdapat data X_{1/2 n}

L = tepi bawah kelas median

c = lebar kelas

n = banyaknya data

F = frekuensi kumulatif kurang dari sebelum kelas median

f = frekuensi kelas median

Contoh :

Perhatikan data di bawah ini !

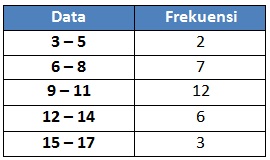
Tabel di atas menyajikan berat badan (dalam Kg) dari 30 balita yang ditimbang saat kegiatan Posyandu di Desa Suka Makmur. Median dari data tersebut adalah ....

Jawab:

Banyak data : 30

Letak Median : n / 2 = 30 / 2 = 15 ( data ke-15 maka terletak di rentang data 9 - 11 )

tepi bawah (L) : 9 - 0,5 = 8,5

panjang kelas (c) : 3

f_k: 9

masuk ke dalam rumus

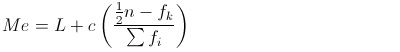
Me = 8,5 + 3 ( (15 - 9) / 12)

Me = 8,5 + 3 (6/12) = 8,5 + 1,5 = 10 kg

Jadi Median dari data tersebut adalah 10 Kg

Untuk lebih memahami tentang pencarian nilai median, coba sobat pintar kerjakan beberapa latihan di halaman berikutnya

Modus (Nilai sering muncul)

Sobat pintar, selanjutnya kita mempelajari apa itu Modus.

Modus ialah nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi. Jika suatu data hanya mempunyai satu modus disebut unimodal dan bila memiliki dua modus disebut bimodal, sedangkan jika memiliki modus lebih dari dua disebut multimodal. Modus dilambangkan dengan Mo.

1. Modus data tunggal

Modus dari data tunggal adalah data yang sering muncul atau data dengan frekuensi tertinggi.

Perhatikan contoh soal berikut ini.

Tentukan modus dari data 2, 1, 4, 1, 1, 5, 7, 8, 9, 5, 5, 10

Jawab: Data yang sering muncul adalah 1 (muncul sebanyak 3 kali) dan 5 (muncul sebanyak 3 kali) . Jadi modusnya adalah 1 dan 5 (bimodal).

2. Modus data kelompok

Modus data kelompok dirumuskan sebagai berikut:

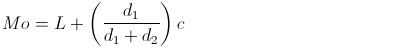
Keterangan:

L = tepi bawah kelas modus

c = lebar kelas

d1 = selisih frekuensi kelas modus dengan kelas sebelumnya

d2 = selisih frekuensi kelas modus dengan kelas sesudahnya

Quartil

Seperti yang sudah dibahas sebelumnya sobat pintar, bahwa median membagi data yang telah diurutkan menjadi dua bagian yang sama banyak. Adapun kuartil adalah membagi data yang telah diurutkan menjadi empat bagian yang sama banyak.

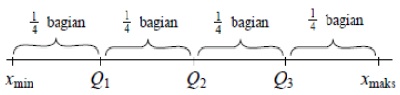
Keterangan :

Xmin = data terkecil

Xmax = data terbesar

Q1 = kuartil ke - 1

Q2 = kuartil ke - 2

Q3 = kuartil ke - 3

 

1. Kuartil data tunggal

Urutkan data dari yang kecil ke yang besar, kemudian tentukan kuartil dengan rumus sebagai berikut:

Contoh:

Tentukan Q1, Q2, dan Q3 dari data : 3, 4, 7, 8, 7, 4, 8, 4, 6, 9, 10, 8, 3, 7, 12.

Jawab:

Langkah 1:

urutkan data dari kecil ke besar sehingga diperoleh 3, 3, 4, 4, 4, 6, 7, 7, 7, 8, 8, 8, 9, 10, 12.

Langkah 2:

Letak data Q1 = 1(15+1)/4 = 4

Jadi Q1 terletak pada data ke-empat yaitu 4

Langkah 3:

Letak data Q2 = 2(15+1)/4 = 8

Jadi Q2 terletak pada data ke-delapan yaitu 7

Langkah 4:

Letak data Q1 = 3(15+1) / 4 = 12

Jadi Q3 terletak pada data ke-duabelas yaitu 8

2. Kuartil data kelompok

Nilai kuartil dirumuskan sebagai berikut:

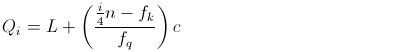
Keterangan:

Qi = kuartil ke-i (1, 2, atau 3)

L = tepi bawah kelas kuartil ke-i

n = banyaknya data

F = frekuensi kumulatif kelas sebelum kelas kuartil

c = lebar kelas

f = frekuensi kelas kuartil

Desil

Sobat pintar, pada materi ini kali ini merupakan kelanjutan dari kuartil.

Kalau desil berfungsi membagi data menjadi sepuluh bagian yang sama besar. Setiap n data terurut dibagi menjadi 10 bagian, sehingga terdapat 9 nilai desil. Ilustrasi pembagian n data terurut menjadi 10 bagian sama banyak dan letak nilai desilnya dapat dilihat pada gambar di bawah.

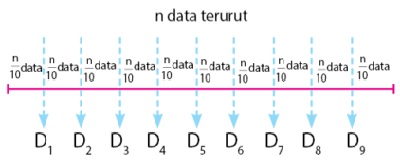
1. Desil untuk data tunggal

Berikut rumus untuk mencari nilai desil data tunggal :

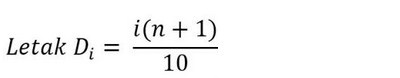
Keterangan :

Di adalah desil ke-i

n adalah banyaknya data

2. Desil untuk data berkelompok

Berikut rumus untuk mencari nilai desil data berkelompok :

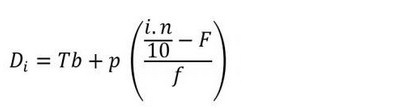
Keterangan :

Di adalah desil ke-i

Tb adalah tepi bawah kelas desil

p adalah panjang kelas

n adalah banyaknya data

F adalah frekuensi kumulatif sebelum kelas desil

f adalah frekuensi kelas desil

 

Contoh :

1. Desil data tunggal

Tentukan desil ke-8 dari data : 6, 3, 8, 9, 5, 9, 9, 7, 5, 7, 4, 5, 8, 3, 7, 6.

Jawab:

n = 16

data terurut = 3, 3, 4, 5, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9, 9.

letak D8 = 8(16+1) / 10 = 13,6

D8 = X13 + 0,6 (X14 – X13)

=8 +0,6(9-8)

= 86

2. Desil data berkelompok

Tentukan nilai D6 dari data berikut :

Jangkauan

Ukuran penyebaran yang paling sederhana (kasar) adalah jangkauan (range) atau rentangan nilai, yaitu selisih antara data terbesar dan data terkecil.

1. Range data tunggal

Untuk range data tunggal dirumuskan dengan:

R = xmaks – xmin

Contoh :

Tentukan range dari data-data di bawah ini.

6, 7, 3, 4, 8, 3, 7, 6, 10, 15, 20

Jawab :

Dari data di atas urutkan terlebih dahulu kemudian diperoleh xmaks = 20 dan xmin = 3 Jadi, R = xmaks – xmin = 20 – 3 = 17

2. Range data kelompok

Untuk data kelompok, nilai tertinggi diambil dari nilai tengah kelas tertinggi dan nilai terendah diambil dari nilai kelas yang terendah.