Sistem Pertidaksamaan Linear Dua Variabel

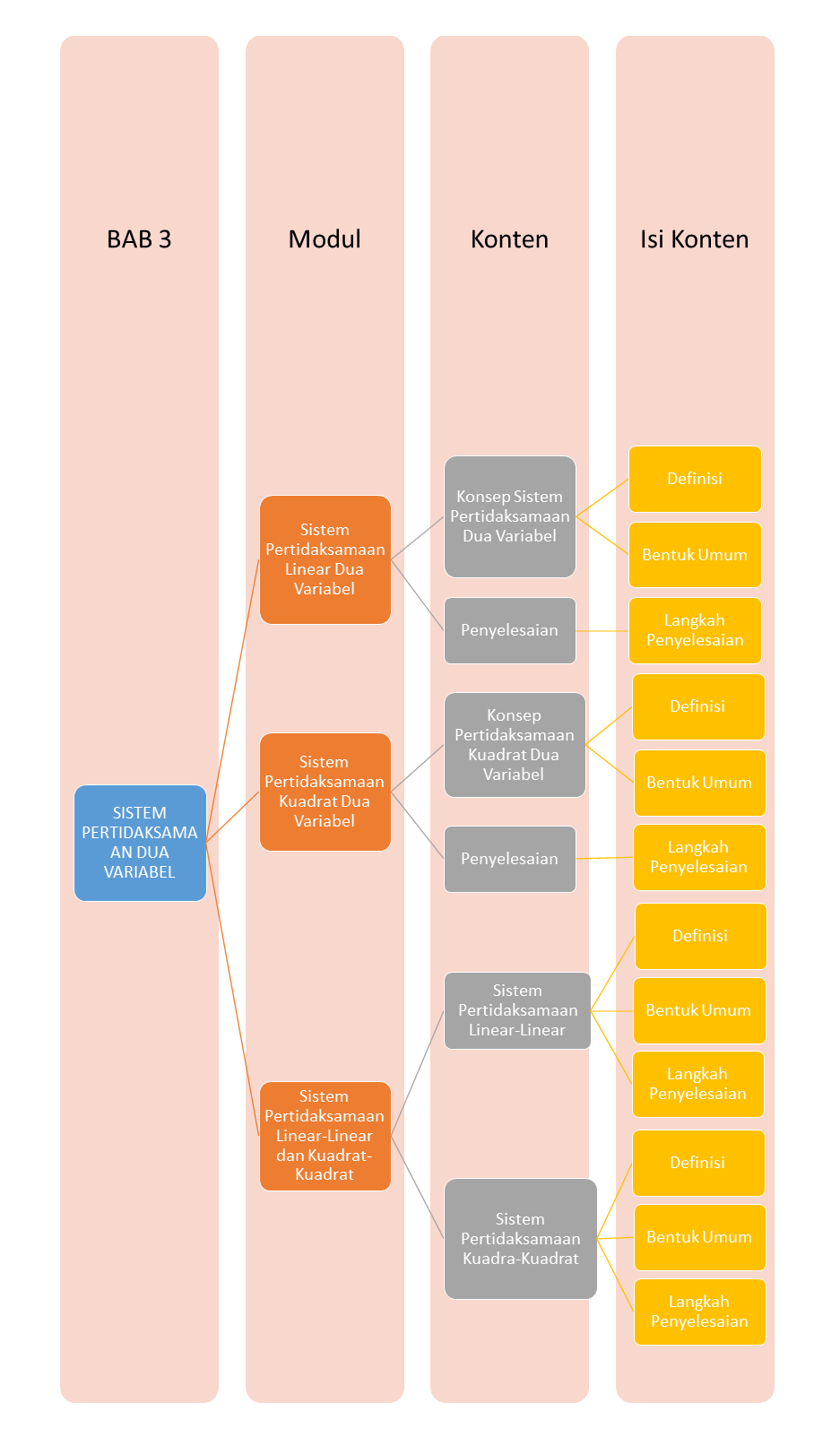
Konsep Sistem Pertidaksamaan Linear Dua Variabel

Sumber : Geogebra.org

Halo Sobat! 
Apakah Sobat Pintar pernah melihat grafik di atas? Unik sekali, bukan? Kira-kira cara membuatnya seperti apa ya?
Nah, sekarang kita akan belajar tentang Sistem Pertidaksamaan untuk membuat grafik-grafik yang unik lho!

Pertidaksamaan Linear Dua Variabel
Pertidaksamaan Linear Dua Variabel merupakan suatu pertidaksamaan yang memuat dua variabel dengan masing-masing variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan.

Bentuk umum Pertidaksamaan Linear Dua Variabel
Bentuk umum dari pertidaksamaan Linear Dua Variabel antara lain:

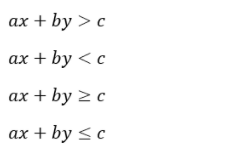
Contoh bentuk sistem pertidaksamaan linear dua variabel :

Konsep Pertidaksamaan Kuadrat Dua Variabel

Pertidaksamaan Kuadrat Dua Variabel

Pertidaksamaan kuadrat dua variabel merupakan suatu pertidaksamaan yang memuat dua variabel dengan salah satu atau kedua variabel maksimal berderajat dua dan dihubungkan dengan tanda ketidaksamaan. Perbedaan pertidaksamaan linear dengan pertidaksamaan kuadrat adalah pada derajat (pangkat) variabelnya.

Bentuk umum Pertidaksamaan Kuadrat Dua Variabel

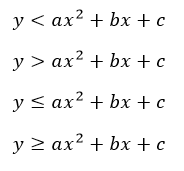
Contoh bentuk sistem pertidaksamaan linear dua variabel :

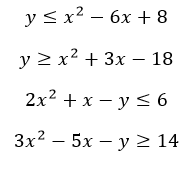
Konsep Sistem Pertidaksamaan Linear Kuadrat

Dalam sistem pertidaksamaan kuadrat dua variabel terdapat 2 macam sistem, yaitu

• Sistem pertidaksamaan linear-kuadrat
• Sistem pertidaksamaan kuadrat-kuadrat

Sistem Pertidaksamaan Linear Kuadrat

Sistem pertidaksamaan linear-kuadrat berarti suatu sistem pertidaksamaan yang terdiri atas pertidaksamaan linear dan pertidaksamaan kuadrat.
Bentuk umum Pertidaksamaan linear Kuadrat

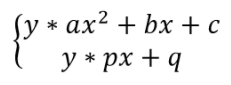
Dengan * merupakan tanda pertidaksamaan

Langkah-langkah membuat sketsa grafik sistem pertidaksamaan linear-kuadrat sebagai berikut: 

1. Sketsa grafik masing-masing persamaan persamaan linear dan persamaan kuadrat 
2. Beri arsiran untuk daerah penyelesaian masing-masing pertidaksamaan. 
3. Tentukan daerah penyelesaian yang merupakan irisan atau perpotongan daerah yang memenuhi sistem pertidaksamaan terkait. 
4. Lakukan pengujian kebenaran dengan memilih titik uji di dalam daerah penyelesaian tersebut