Materi Matematika - Relasi dan Fungsi Kelas 8 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, Ini nih ada Peta Belajar Bersama Matematika di BAB Ketiga
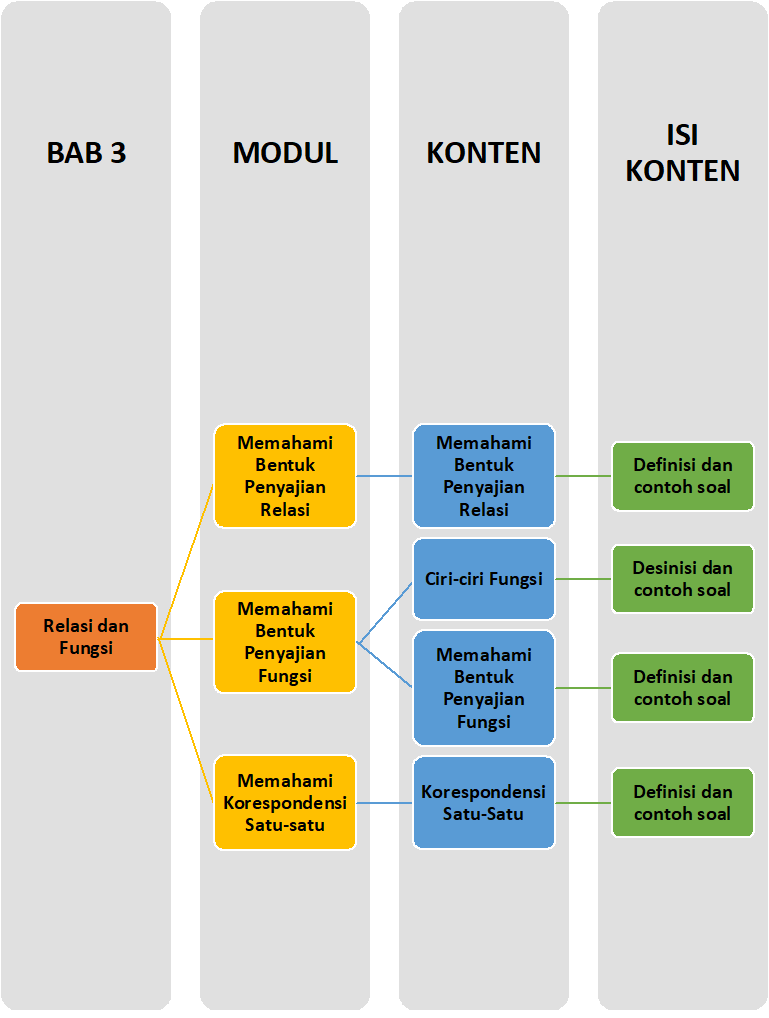
Yuk belajar bersama.....
Memahami Bentuk Penyajian Relasi

Nah, Sobat Pintar. Di bagian ini kita akan bersama memelajari tentang bentuk penyajian relasi.
Perhatikan Contoh berikut ini :
Hasil pengambilan data mengenai pelajaran yang disukai oleh lima siswa kelas VIII diperoleh seperti pada tabel berikut.
Tabel Data pelajaran yang disukai siswa kelas VIII
Permasalahan pada Tabel di atas dapat dinyatakan dengan diagram panah, diagram Kartesius, dan himpunan pasangan berurutan seperti berikut ini.
Misalkan A = {Abdul, Budi, Candra, Dini, Elok}, B = {Matematika, IPA, IPS, Bahasa Inggris, Kesenian, Keterampilan, Olahraga}, dan “pelajaran yang disukai” adalah relasi yang menghubungkan himpunan A ke himpunan B.
Cara 1: Diagram Panah
Gambar dibawah ini menunjukkan relasi “pelajaran yang disukai” dari himpunan A ke himpunan B. Arah panah menunjukkan anggota-anggota himpunan A yang berelasi dengan anggota-anggota tertentu pada himpunan B.
Gambar Diagram panah kesukaan
Cara 2: Diagram Kartesius
Cara yang kedua untuk menyatakan relasi antara himpunan A dan B adalah menggunakan diagram Kartesius. Anggota-anggota himpunan A berada pada sumbu mendatar dan anggota-anggota himpunan B berada pada sumbu tegak. Setiap pasangan anggota himpunan A yang berelasi dengan anggota himpunan B dinyatakan dengan titik atau noktah. Gambar dibawah ini menunjukkan diagram Kartesius dari relasi “pelajaran yang disukai” dari data pada tabel diatas.
Gambar Diagram Kartesius kesukaan
Cara 3: Himpunan Pasangan Berurutan
Apabila data pada Tabel 3.2 dinyatakan dengan pasangan berurutan, maka dapat ditulis sebagai berikut.
Himpunan pasangan berurutan dari himpunan A ke himpunan B adalah
{(Abdul, Matematika), (Abdul, IPA), (Budi, IPA), (Budi, IPS), (Budi, Kesenian), (Candra, Keterampilan), (Candra, Olahraga), (Dini, Bahasa Inggris), (Dini, Kesenian), (Elok, Matematika), (Elok, IPA), (Elok, Keterampilan)}
Uraian di atas menunjukkan macam-macam cara yang bisa digunakan untuk menyatakan relasi dari himpunan A ke himpunan B.
Ciri-ciri Fungsi

Apa yang Sobat Pintar tahu tentang fungsi? Berikut penjelasan tentang fungsi.
Fungsi merupakan salah satu konsep penting dalam matematika. Dengan mengenali fungsi atau hubungan fungsional antar unsur-unsur matematika, kita bisa lebih mudah memahami suatu permasalahan, dan menyelesaikannya. Oleh karena itu, memahami fungsi merupakan hal yang sangat diharapkan dalam belajar matematika.
Pertama kali, mari kita pelajari ciri-ciri dari suatu fungsi, sebelumnya mari kita ketahui apa saja ciri-ciri fungsi:
- Himpunan A dan himpunan B bukan himpunan kosong.
- Pasangan setiap anggota himpunan A tidak boleh lebih dari satu.
- Setiap anggota himpunan A harus mempunyai pasangan di himpunan B.
- Anggota himpunan B boleh tidak mempunyai pasangan di A atau mempunyai pasangan lebih dari satu.
Untuk memahami ciri-ciri dari suatu fungsi, sebaiknya perhatikan uraian berikut. Himpunan pasangan berurutan yang bisa menjadi fungsi dari B = {a, b} ke A = {1, 2, 3} adalah:
{(a, 1), (b, 1)}
{(a, 1), (b, 2)}
{(a, 1), (b, 3)}
{(a, 2), (b, 1)}
{(a, 2), (b, 2)}
{(a, 2), (b, 3)}
{(a, 3), (b, 1)}
{(a, 3), (b, 2)}
{(a, 3), (b, 3)}
Perlu kalian ketahui, dalam konteks fungsi dari himpunan A ke himpunan B, maka himpunan A disebut Daerah Asal atau Domain dan himpunan B disebut dengan daerah Kawan atau Kodomain dari fungsi tersebut. Sedangkan himpunan bagian dari himpunan B yang semua anggotanya mendapat pasangan di anggota himpunan A disebut Daerah Hasil atau Range.
Contoh Soal :
Misalkan A = {2, 4, 6, 8, 10, 12, 14, 16}, B = {1, 5, 9}
Relasi yang didefinisikan adalah "anggota A dua kali anggota B”. Apakah relasi dari A ke B termasuk fungsi?
Penyelesaian :
Untuk mengetahui apakah relasi dari A ke B termasuk fungsi atau bukan, lakukan prosedur berikut.
Diketahui relasi dari A ke B adalah anggota A dua kali anggota B, Maka dapat dituliskan dalam bentuk pasangan berurutan sebagai berikut: {(2, 1), (10, 5)}.
Coba kita perhatikan kembali beberapa anggota A lainnya yang tidak mempunyai pasangan ke B, yakni:
Beberapa anggota A yang tidak mempunyai pasangan di B adalah 4, 6, 8, 12, 14, dan 16.
Hal ini karena tidak ada bilangan x di B demikian sehingga “4 dua kali anggota B”, “6 dua kali anggota B”, “8 dua kali anggota B”, “12 dua kali anggota B”, “14 dua kali anggota B”, dan “16 dua kali anggota B”.
Dengan demikian relasi ini juga bukan fungsi dari A ke B, karena ada beberapa anggota A yang tidak mempunyai pasangan di B.
Korespondensi Satu-Satu

Agar Sobat Pintar memahami pengertian tentang korespondensi satu-satu, perhatikan Gambar di bawah ini. Perhatikan deretan rumah di suatu daerah. Setiap rumah memiliki nomor rumah tertentu yang berbeda dengan nomor rumah di daerah tersebut. Mungkinkah satu rumah memiliki dua nomor rumah? Atau mungkinkah dua rumah memiliki nomor rumah yang sama? Tentu saja jawabannya tidak. Hubungan antara rumah dan nomor rumah merupakan suatu fungsi yang disebut korespondensi satu-satu.

Gambar Deretan rumah
Untuk lebih memahami tentang korespondensi satu-satu, coba perhatikan uraian berikut.
Perhatikan contoh korespondensi satu-satu pada tabel 3.9 nomor 1. Diketahui himpunan A = {1, 2, 3,} dan himpunan B = {a, b, c}. Relasi dari himpunan A ke himpunan B yang merupakan korespondensi satu-satu dapat dijabarkan sebagai berikut.
Tabel Banyak korespondensi satu-satu dari himpunan A ke himpunan B
Berdasarkan uraian pada Tabel diatas, banyaknya korespondensi satu-satu yang mungkin dari himpunan A ke himpunan B adalah sebanyak 6.
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








