Materi Matematika - Teorema Pythagoras Kelas 8 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, Ini nih ada Peta Belajar Bersama Matematika di BAB Keenam
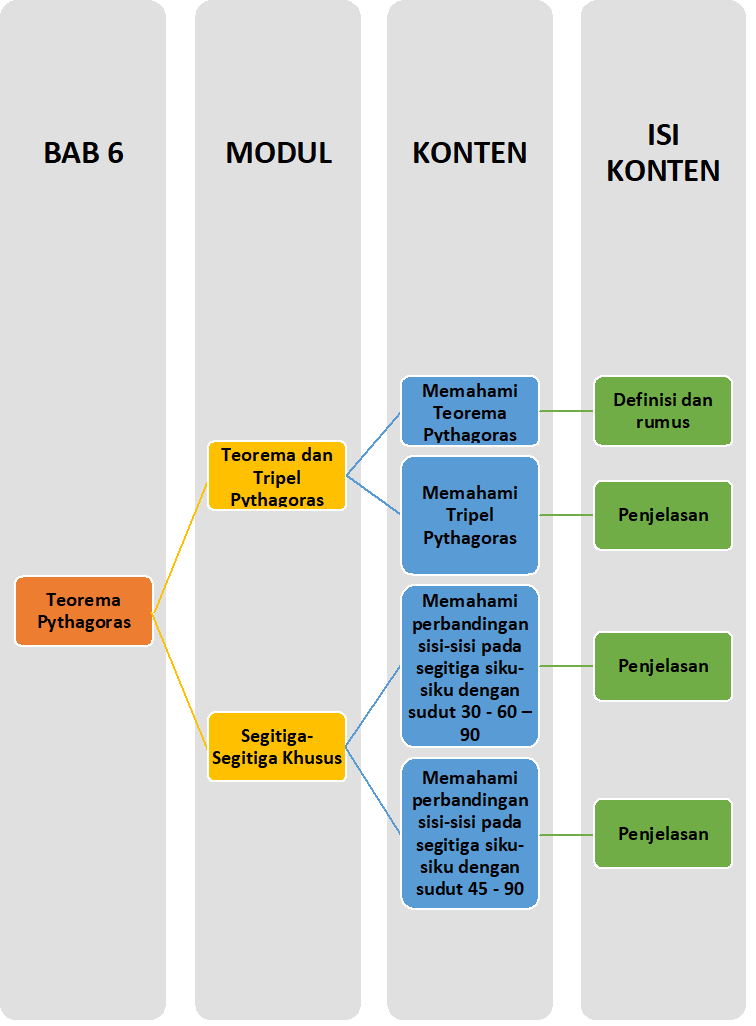
Yuk belajar bersama....
Memahami Teorema Pythagoras

Pythagoras menyatakan bahwa : “Untuk setiap segitiga siku-siku berlaku kuadrat panjang sisi miring (Hipotenusa) sama dengan jumlah kuadrat panjang sisi siku-sikunya.”
Jika c adalah panjang sisi miring/hipotenusa segitiga, a dan b adalah panjang sisi siku-siku. Berdasarkan teorema Pythagoras di atas maka diperoleh hubungan:
c2= a2 + b2
Dalil pythagoras di atas dapat diturunkan menjadi:
a2 = c2 – b2
b2 = c2 – a2
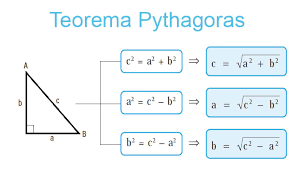
Catatan : Dalam menentukan persamaan Pythagoras yang perlu diperhatikan adalah siapa yang berkedudukan sebagai hipotenusa/sisi miring.
Memahami perbandingan sisi-sisi pada segitiga siku-siku dengan sudut 30 - 60 - 90

Perhatikan gambar di bawah ini!
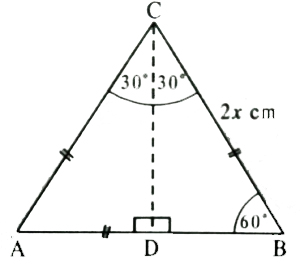
Segitiga ABC diatas merupakan segitiga sama sisi dengan AB = BC = AC = 2x cm dan sudut A = sudut B = sudut C = 60o. Dikarenakan CD tegak lurus AB, maka CD merupakan garis tinggi sekaligus garis bagi sudut C, sehingga
sudut ACD = sudut BCD =30o. Dan diketahui sudut ADC = sudut BDC = 90o. Titik D merupakan titik tengah AB, dimana panjang AB = 2x cm sehingga panjang BD = x cm
Perhatikanlah segitiga CBD. Kita gunakan teorema pythagoras maka diperoleh
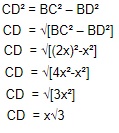
Dengan demikian diperoleh perbandingan sebagai berikut:
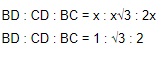
Perbandingan diatas dapat digunakan untuk menyelesaikan soal yang berkaitan dengan segitiga siku-siku khusus. Untuk lebih detailnya, berikut adalah tabel yang berisi tentang panjang sisi-sisi pada segitiga siku-siku 30o - 60o - 90o.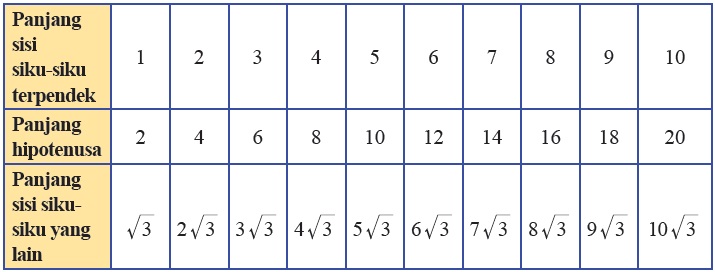
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








