Materi Matematika - Persamaan dan Pertidaksamaan Linear Satu Variabel Kelas 8 - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, ini nih, ada Peta Belajar Bersama Matematika di bab Keempat
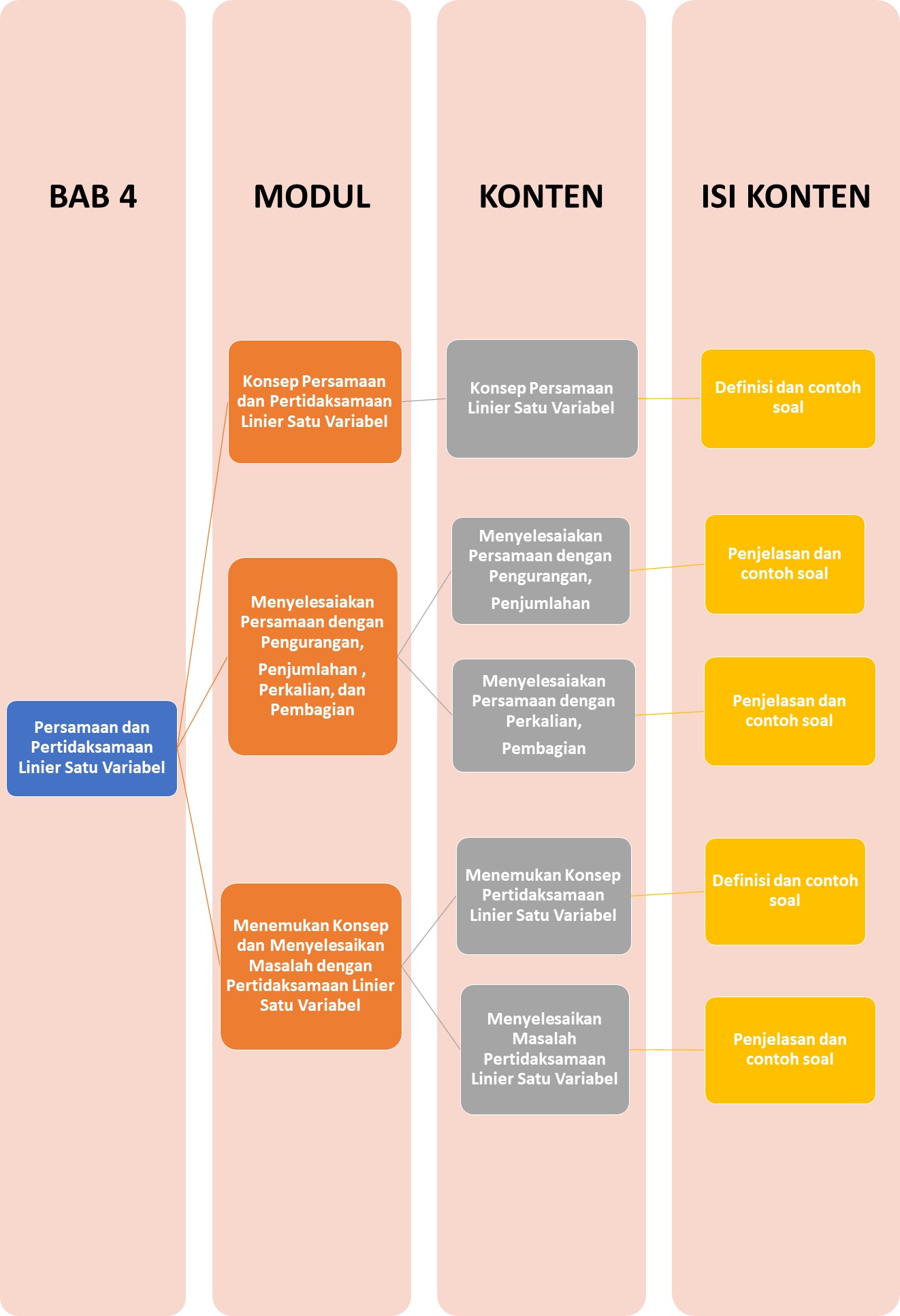
Yuk, mulai belajar bersama!
Persamaan Linear Satu Variabel

Nah, Sobat Pintar. DI bagian ini kita akan bersama memelajari tentang Persamaan Linear Satu Variabel.
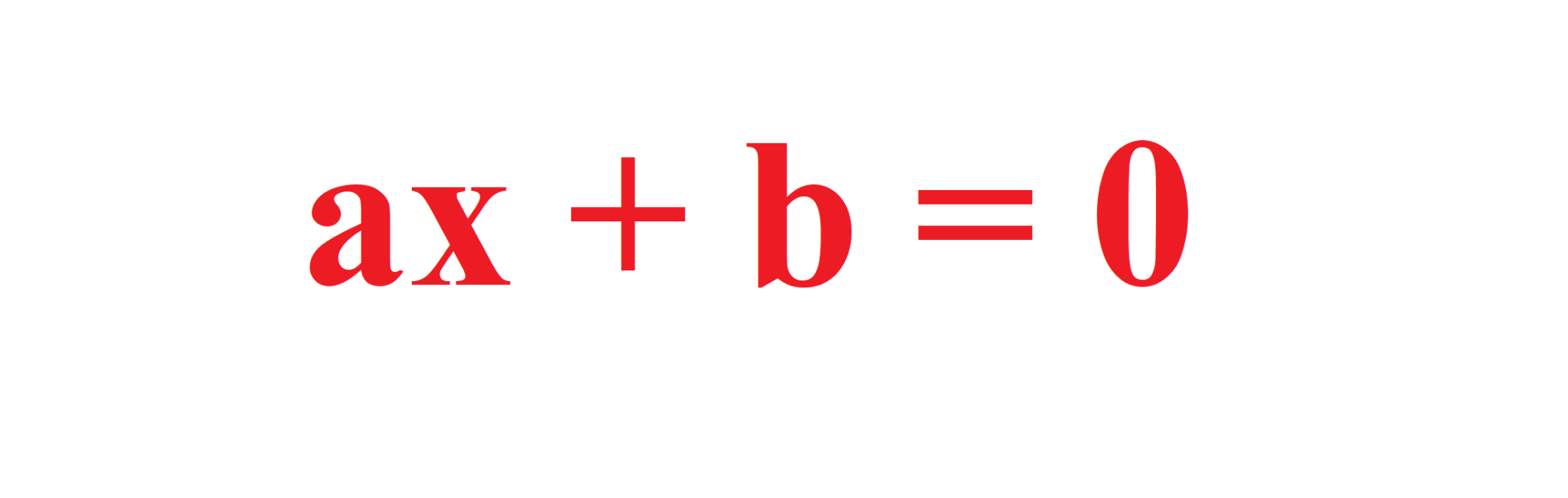
Persamaan Linear Satu Variabel (SPLSV) adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan (=) dan hanya mempunyai satu variabel berpangkat satu. Bentuk umum persamaan linier satu variabel adalah ax + b = 0, dengan a dan b bilangan bulat bukan nol
Kalimat terbuka adalah kalimat yang belum dapat ditentukan nilai kebenarannya, bernilai benar saja atau salah saja karena memiliki unsur yang belum diketahui nilainya.
Variabel adalah simbol/lambang yang mewakili sebarang anggota suatu himpunan semesta. Variabel biasanya dilambangkan dengan huruf kecil.
Contoh :
1. Dua dikurang m sama dengan satu.
Merupakan kalimat terbuka karena memiliki variabel yaitu m.
2. y adalah bilangan prima yang lebih dari empat.
Merupakan kalimat terbuka yang memiliki variabel y.
3. x + 7 = 9.
Merupakan kalimat terbuka karena memiliki variabel x.
4. 4 + b > 10.
Merupakan kalimat terbuka karena memiliki variabel b.
5. 2a - 4 < 31
Merupakan kalimat terbuka karena memiliki variabel a.
Suatu kalimat terbuka yang memiliki variabel harus diganti oleh satu atau lebih anggota dari himpunan semesta yang didefinisikan, sehingga kalimat terbuka yang diberikan akan menjadi benar. Pengganti variabel tersebut dinamakan selesaian. Himpunan semua selesaian dalam kalimat terbuka disebut himpunan selesaian.
Persamaan adalah kalimat terbuka yang terdapat tanda sama dengan (=). Lantas, bagaimana bentuk persamaan linear satu variabel? Untuk mengetahui lebih lanjut, mari kita gali informasi.
Untuk menulis kalimat sebagai suatu persamaan, kalian harus mencari kata kunci seperti adalah atau sama dengan untuk menentukan letak tanda sama dengan. Perhatikan contoh berikut.
Contoh :
1. Tuliskan kalimat berikut menjadi suatu persamaan.
a. Jumlah suatu bilangan n dan 7 adalah 15.
Jumlah suatu bilangan n dan 7 adalah 15.
n + 7 = 15
Jadi, persamaannya adalah n + 7 = 15.
b. Selisih bilangan y dan 7 adalah 3.
y - 7 = 3
Jadi, persamaannya adalah y - 7 = 3.
c. Hasil kali bilangan g dan 5 sama dengan 30.
Hasil kali bilangan g dan 5 sama dengan 30.
5g = 30
Jadi, persamaannya adalah 5g = 30.
Menyelesaikan Persamaan Menggunakan Penjumlahan atau Pengurangan

Hallo Sobat Pintar! Kalian masih bingung gak sih gimana cara menyelesaikan Persamaan Linier satu Variabel? Berikut penjelasannya agar kalian gak bingung lagi yuk kita simak.
Dalam menyelesaikan persamaan linear satu variabel, tujuannya adalah menyederhanakan persamaan untuk menyisakan variabel saja di salah satu sisi. Setiap langkah yang digunakan untuk menyederhanakan persamaan menghasilkan persamaan ekuivalen. Apakah yang dimaksud dengan persamaan ekuivalen?
Perhatikan persamaan-persamaan berikut.
1. x + 1 = 3
2. x + 2 = 4
3. 2x - 2 = 6
Bagaimanakah himpunan selesaian dari ketiga persamaan di atas? Ketiga persamaan tersebut memiliki himpunan selesaian yang sama. Persamaan-persamaan di atas disebut dengan persamaan yang ekuivalen atau persamaan yang setara.
Untuk memahami bagaimana persamaan yang ekuivalen digunakan untuk menentukan himpunan selesaian suatu persamaan mari kita simak contoh soal dibawah ini
Contoh Soal :
1. Tentukan Penyelesaian dari persamaan berikut.
a. x - 4 = 7
b. 8 = x - 7
2. Tentukan himpunan selesaian dari 12 + x = 40
3. Andi memakan 8 kue baruasa dan Nyoman memakan 11 kue baruasa dari kemasan yang baru dibuka. Mereka berdua menyisakan 23 kue baruasa di dalam kemasan. Tulis persamaan dan tentukan selesaiannya untuk mengetahui banyaknya kue baruasa dalam kemasan semula.
Penyelesaian :
1. a. x - 4 = 7
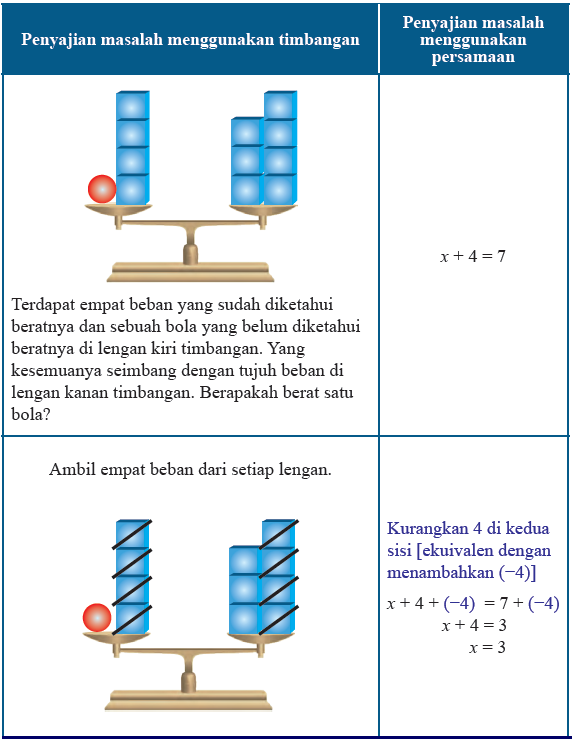
b. 8 = x - 7
2. 12 + x = 40
12 - 12 + x = 40 - 12
x = 28
Periksa
12 + x = 40
12 + (28) = 40
40 = 40 (benar)
Jadi, himpunan Penyelesaiannya adalah {28}.
3. Kata-kata Banyak kue semula dikurangi banyak kue yang dimakan Andi dikurangi banyak kue yang dimakan Nyoman sama dengan
banyak kue yang tersisa.
Variabel Misalkan b adalah banyak kue dalam kemasan semula
Persamaan b - 8 - 11 = 23
b - 8 - 11 = 23
b - 19 = 23
b - 19 + 19 = 23 + 19
b = 42
Jadi, banyak kue dalam kemasan semula adalah 42 kue.
Mengenal Konsep Pertidaksamaan Linear Satu Variabel

Dalam materi sebelumnya, Sobat Pintar telah mempelajari bagaimana menyatakan dan menyelesaikan persamaan linear satu variabel. Di Kegiatan ini, kalian akan mempelajari pertidaksamaan linear satu variabel. Perhatikan tabel berikut.
Tabel Persamaan dan Pertidaksamaan
Amati perbedaan antara kedua kolom. Terlihat bahwa kedua sisi pada pertidaksamaan linear bukan dipisahkan oleh tanda sama dengan, namun dipisahkan oleh tanda pertidaksamaan, <, >, <, atau >.
Selesaian persamaan x = 3 dapat disajikan dalam bentuk titik tunggal pada garis bilangan.
Bagaimana dengan himpunan selesaian dari x < 3? Himpunan selesaian dari pertidaksamaan tersebut merupakan nilai dari variabel sehingga membuat pertidaksamaan menjadi pernyataan yang benar. Dalam beberapa kasus, himpunan selesaian sudah ditentukan terlebih dahulu termasuk anggota himpunan bilangan yang mana.
Dalam kasus jika himpunan selesaian dari pertidaksamaan x < 3 adalah semua bilangan real, kita bisa menyatakan dengan “semua bilangan real yang kurang dari atau sama dengan 3.” Oleh karena anggota himpunan selesaiannya tak terhingga banyaknya, maka x tidak bisa kita sebutkan satu-satu. Sehingga kita bisa membuat grafik berupa garis bilangan. Notasi interval atau notasi pembentuk himpunan sebagai penyajian himpunan selesaian.
Perhatikan beberapa pertidaksamaan dan himpunan selesaiannya dalam bentuk garis bilangan berikut.
Perhatikan titik atau bulatan pada garis bilangan. Jika bilangan pada titik igambarkan dengan bulatan penuh, maka titik tersebut termasuk anggota himpunan selesaian. Jika bilangan pada titik digambarkan dengan bulatan kosong, maka titik tersebut tidak termasuk dalam anggota himpunan selesaian.
Contoh Soal :
Tulislah masalah berikut menjadi sebuah pertidaksamaan linear satu variabel.
Kalian ingin menentukan nilai x, sedemikian sehingga luas jajargenjang di samping tidak kurang dari 40 satuan luas.
Penyelesaian :
Diketahui alas jajargenjang adalah 5 satuan.
Tinggi jajargenjang adalah y + 7 satuan.
Luas jajargenjang yang diminta tidak kurang dari 40 satuan luas.
alas x tinggi < 40
5 x (y + 7) < 40
5y + 35 < 40
Jadi, pertidaksamaan dari masalah di atas adalah 5y + 35 < 40.
Menyelesaikan Masalah Pertidaksamaan Linear Satu Variabel

Perbedaan penting antara persamaan linear satu variabel dengan pertidaksamaan linear satu variabel ditunjukkan ketika kita mengali atau membagi kedua sisi pertidaksamaan dengan bilangan bukan nol.
a. Ketika kalian mengalikan atau membagi kedua sisi dengan bilangan positif, maka tanda ketidaksamaan tidak berubah. Perhatikan tabel berikut.

Sifat ini juga berlaku untuk < dan >
b. Ketika kalian mengalikan atau membagi kedua sisi dengan bilangan negatif, maka tanda ketidaksamaan berubah. Perhatikan tabel berikut..

Sifat ini juga berlaku untuk < dan >
Untuk lebih memahami tentang masalah pertidaksamaan linear satu variabel mari kita simak contoh soal dibawah ini
Contoh Soal :
Selesaikan pertidaksamaan x - 4 < - 2. Gambar selesaiannya dalam garis bilangan dan tuliskan selesaiannya dalam notasi interval.
Penyelesaian :
x - 4 < - 2
x - 4 + 4 < - 2 + 4
x < 2
Jadi, selesaiannya adalah x < 2 atau (-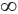 , 2).
, 2).

Contoh Soal :
Tentukan himpunan selesaian dari peridaksamaan linear berikut dengan x adalah bilangan bulat.
-6(x - 3) > 2 - 2 (x - 8)
Penyelesaian :
-6(x - 3) > 2 - 2 (x - 8)
-6x + 18 > 2 - 2x + 16
-6x + 18 > 18 - 2x
-6x + 2x + 18 > 18 - 2x + 2x
-4x + 18 > 18
-4x + 18 -18 > 18 -18
-4x > 0
-4x/-4 < 0/-4
x < 0
Jadi, himpunan selesaian dari pertidaksamaan -6(x - 3) > 2 - 2 (x - 8) adalah
Contoh Soal :
Pak Ferdy memiliki sebuah mobil box pengangkut barang dengan daya angkut tidak lebih dari 800 kg. Berat Pak Fredy adalah 60 kg dan dia akan mengangkut kotak barang yang setiap kotak beratnya 20 kg. Tentukan pertidaksamaan dari situasi di atas. Tentukan banyak kotak paling banyak yang dapat diangkut oleh Pak Fredy dalam sekali pengangkutan.
Penyelesaian :
a. Misalkan: x = banyaknya kotak barang yang diangkut dalam mobil box. Sehingga, pertidaksamaan dari situasi tersebut adalah sebagai berikut.
Banyak kotak dikali berat tiap kotak ditambah berat Pak Ferdy tidak lebih dari daya angkut mobil.
x x 20 + 60 < 800
Jadi, pertidaksamaan dari situasi Pak Ferdy adalah 20 x + 60 < 800
b. Untuk menentukan banyak kotak paling banyak yang dapat diangkut oleh mobil box Pak Ferdy adalah dengan menentukan selesaian pertidaksamaan.
20 x + 60 < 800
20 x + 60 - 60 < 800 - 60
20 x < 740
x < 37
x paling besar yang memenuhi pertidaksamaan x < 37 adalah 37.
Jadi, banyak kotak yang dapat diangkut Pak Fredy dalam sekali pengangkutan paling banyak 37 kotak.
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








