Barisan dan Deret

Konsep Pola Bilangan

^{Sumber : lingkarwarna.com}

Pernahkah Sobat Pintar mengamati urutan nomor rumah di kompleks rumah kalian?

Apakah nomor rumahnya berpola bilangan asli sesuai urutan, atau rumah sebelah kiri menggunakan nomor rumah ganjil dan sebelah kanan menggunakan nomor rumah genap?

Nah! Materi yang akan kita bahas kali ini berhubungan dengan pola pada bilangan.

Pengertian Pola Bilangan

Pola bilangan yaitu aturan yang digunakan untuk membuat suatu kelompok bilangan.

Macam-macam Pola Bilangan

Pola bilangan dapat dikelompokkan menjadi beberapa macam, diantaranya:

Pola Bilangan Ganjil

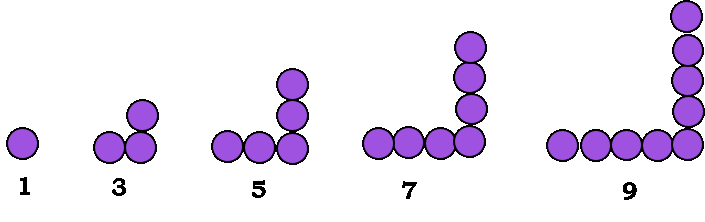
Berdasarkan pola di atas, terbentuk pola bilangan ganjil yaitu: 1, 3, 5, 7, 9.

Rumus bilangan ke-n pada pola bilangan ganjil, yaitu: 2n – 1.

Sedangkan jumlah n bilangan ganjil pertama, yaitu: n².

Pola Bilangan Genap

Berdasarkan pola di atas, terbentuk pola bilangan genap yaitu: 2, 4, 6, 8. 

Rumus bilangan ke-n pada pola bilangan genap, yaitu: 2n. 

Sedangkan jumlah n bilangan genap pertama, yaitu: n(n+1). 

Pola Garis Lurus

Pola garis lurus yaitu suatu bilangan yang digambarkan dengan noktah mengikuti pola garis lurus.

Contoh :

Pola Persegi Panjang

Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: n(n+1). 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Persegi

Berdasarkan pola di atas, terbentuk pola persegi panjang dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: n². 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Segitiga

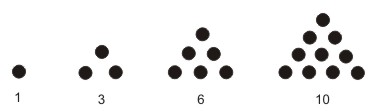
Berdasarkan pola di atas, terbentuk pola segitiga  dengan susunan bilangan 2, 6, 12, 20. 

Rumus bilangan ke-n pada pola persegi panjang, yaitu: 

Sedangkan jumlah n suku pertamanya, yaitu:

Pola Segitiga Pascal

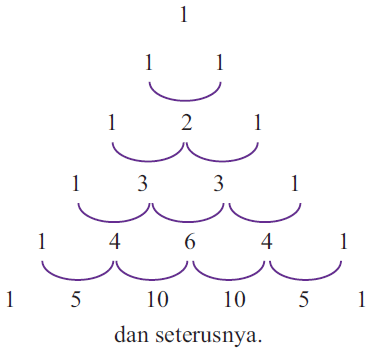
Pola di atas merupakan pola dari segitiga pascal. Segitiga pascal digunakan untuk menentukan koefisien dari polinomial. 

Koefisiennya dapat ditentukan dengan rumus : (a+b)ⁿ. 

Sedangkan jumlah bilangan pada segitiga pascal baris ke-n, yaitu: 2^n-1.

Barisan Aritmetika

^{Sumber: m4th-lab.net}

Barisan dan deret yang sudah kita pelajari sebelumnya akan kita bahas kembali pada materi kali ini.

Seperti yang Sobat Pintar ketahui bahwa suatu barisan ataupun deret terbentuk oleh aturan tertentu yang dikelompokkan menjadi dua, yaitu: Aritmetika dan Geometri.

Kita akan belajar mengenai barisan dan deret aritmetika terlebih dahulu ya, Sobat Pintar.

Barisan Aritmetika adalah barisan bilangan yang memiliki beda atau selisih tetap antara dua suku yang berurutan.

Rumus untuk menentukan suku ke-n dari barisan aritmetika dapat dituliskan:

U_n = a + (n – 1)b

Keterangan:

U_n = Suku ke-n

a = suku pertama

b = beda / selisih

n = banyaknya suku.

Beda atau selisih dari barisan aritmetika dapat dicari dengan cara:

b = U_n – U_n-1

Barisan Geometri

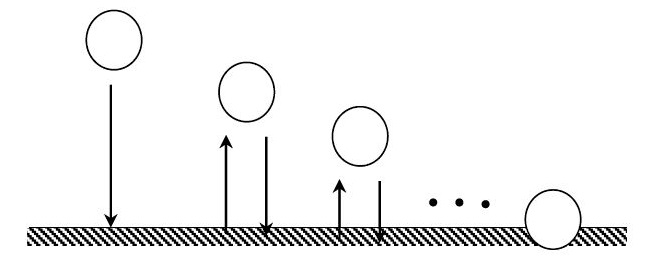
^{Sumber : materimatematika.com}

Bola yang memantul semakin lama tinggi pantulannya akan semakin berkurang, hal ini akan membentuk sebuah pola barisan geometri lho, Sobat Pintar!

Jadi barisan geometri sendiri itu apa sih?

Yuk, langsung simak pembahasannya ya!

Barisan Geometri adalah barisan bilangan dimana dua suku yang berurutan memiliki perbandingan yang bernilai tetap. Perbandingan dalam barisan geometri disebut rasio (r).

Barisan geometri dapat dinyatakan sebagai berikut:

U_n = a.r^n-1

Keterangan :

U_n = suku ke-n

a = suku pertama

r = rasio

n = banyaknya suku

Rasio dari barisan geometri dapat dicari dengan cara:

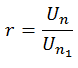
Pertumbuhan dan Peluruhan

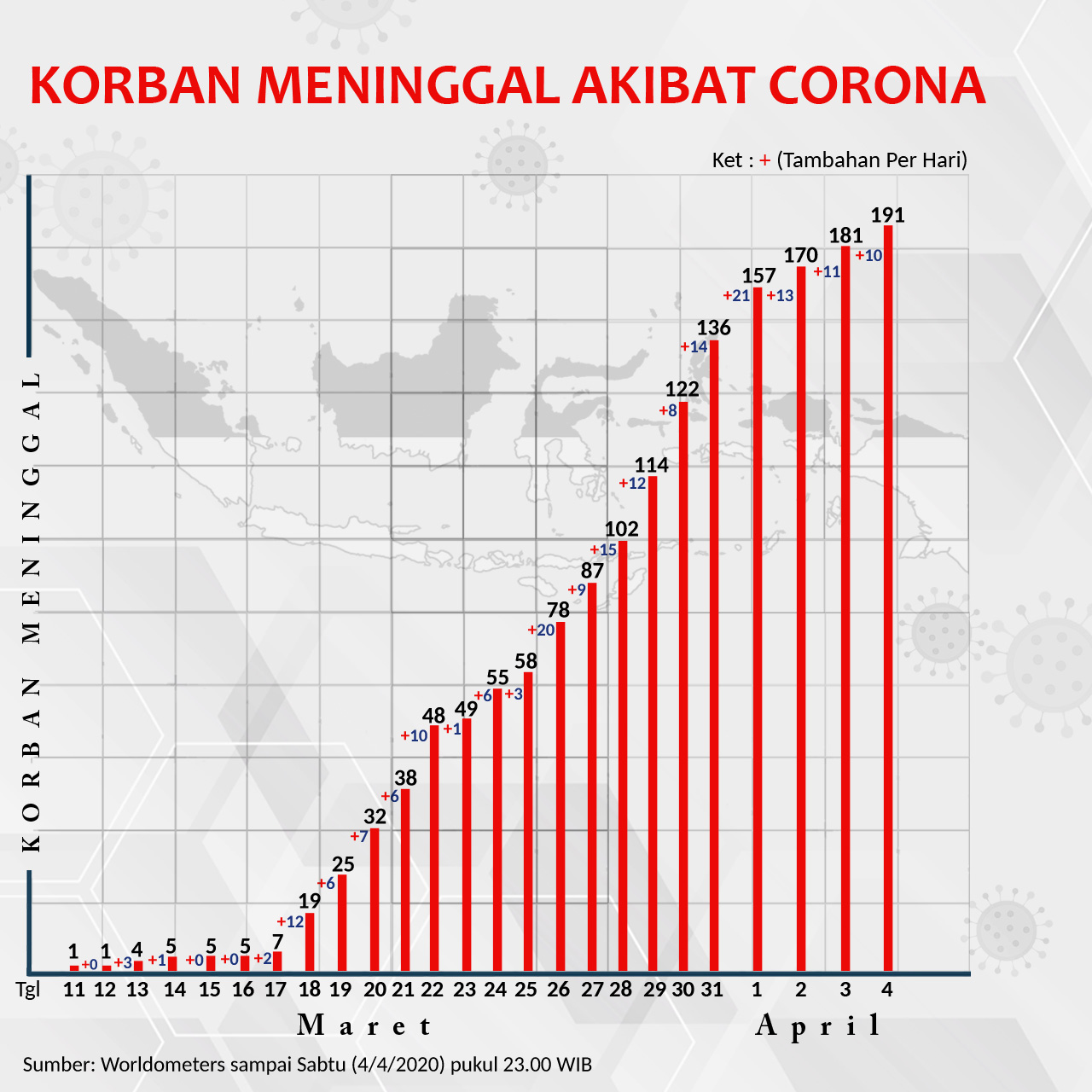
Menurut Sobat Pintar, semenjak adanya pandemi covid-19 membuat tingkat kematian penduduk Indonesia menjadi semakin bertambah atau berkurang ya? Atau bahkan semakin banyak bayi yang lahir saat pandemi ini berlangsung?

Nah suatu barisan sendiri dapat bermanfaat untuk menghitung tingkat kematian maupun kelahiran penduduk Indonesia lho, Sobat!

Kita bisa mengetahui kematian atau kelahiran mengalami pertumbuhan atau peluruhan. Seperti materi yang akan kita bahas kali ini, salah satu aplikasi dari barisan adalah mengenai pertumbuhan dan peluruhan.

Yuk, langsung simak pembahasannya ya!

PERTUMBUHAN

Pertumbuhan merupakan konsep barisan aritmetika maupun geometri yang naik, dapat dituliskan:

U₁ < U₂ < U₃ < U₄ < ... < U_n

Rumus untuk menentukan pertumbuhan setelah tahun ke-n, yaitu:

1. Jika diketahui persentase (i): A_n = A_o (1+i)ⁿ
2. Jika diketahui rasio: A_n = A_o(r)ⁿ  dengan r > 1

Keterangan:

A_o = Jumlah objek awal

A_n = Jumlah objek setelah tahun ke-n

i = persentase pertumbuhan

r = rasio pertumbuhan

n = periode waktu.

PELURUHAN

Peluruhan merupakan konsep barisan aritmetika maupun geometri yang turun, dapat dituliskan:

U₁ > U₂ > U₃ > U₄ > ... > U_n

Rumus untuk menentukan peluruhan setelah tahun ke-n, yaitu:

A_n = A_o ( 1 – i )ⁿ

Khusus untuk menentukan peluruhan dari radioaktif, digunakan rumus:

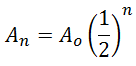
Keterangan

A_n = Jumlah objek setelah periode ke-n

A_o = Jumlah objek awal

i = persentase peluruhan

n = periode waktu.