Matriks

Pengertian Matriks

^{Sumber : desainrumah.modebaca.com}

Halo, sobat pintar! Pernahkah kalian memperhatikan denah ruang kelasmu? Ada berapa baris bangku siswa? Ada berapa kolom bangku siswa?

Materi yang akan kita pelajari hari ini akan berhubungan dengan baris dan kolom lho, Sobat Pintar!

Ya! Kita akan belajar tentang matriks. Apa sih matriks itu? 

Matriks adalah susunan bilangan-bilangan berbentuk persegi panjang yang diatur dalam baris (jajaran) dan kolom (lajur) dengan dibatasi oleh kurung biasa “()” atau kurung siku “[]”.

Bilangan-bilangan yang tersusun dalam matriks disebut elemen (unsur) matriks. Baris sebuah matriks adalah susunan bilangan-bilangan yang mendatar (horizontal), sedangkan kolom adalah susunan bilangan-bilangan yang tegak (vertikal).

Jika suatu matriks diberi nama matriks A, maka secara umum, bentuk matriks A yaitu

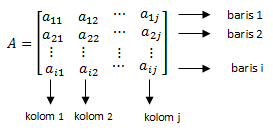
A_ixj artinya matriks A mempunyai baris sebanyak m dan mempunyai kolom sebanyak n.
a₁₁ = elemen baris pertama kolom pertama
a₁₂ = elemen baris pertama kolom kedua
a_1j = elemen baris pertama kolom ke-j
a₂₁ = elemen baris kedua kolom pertama

.

.

.

a_ij = elemen baris ke-i kolom ke-j
 

Penjumlahan dan Pengurangan Matriks

Ternyata matriks juga dapat dioperasikan lho, Sobat. Operasi aljabar pada matriks hanya sebatas penjumlahan, pengurangan, perkalian dan ada juga operasi aljabar khusus yang hanya diterapkan pada matriks. Operasi apa itu? Simak sampai selesai ya!

Penjumlahan Matriks

Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dijumlahkan. Jumlah A dan B dapat dinyatakan dengan A+B.

Contoh :

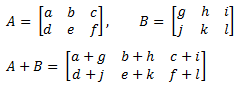
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat penjumlahan, yaitu:

1. Komutatif : A+B = B+A
2. Asosiatif : (A+B)+C = A+(B+C)
3. Identitas : A+O = O+A = A, dengan O adalah matriks nol
4. (A+B)^t = A^t + B^t

Pengurangan Matriks

Jika terdapat dua matriks, misal matriks A dan B, yang memiliki ordo sama, maka elemen-elemen yang seletak dapat dikurangkan. Pengurangan A dan B dapat dinyatakan dengan A – B atau A + (– B).

Contoh :

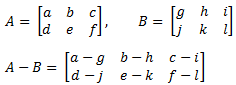
Jika A, B, C merupakan matriks dengan ordo yang sama, maka berlaku sifat pengurangan, yaitu:

1. A – A = O, dengan O adalah matriks nol
2. Identitas : A – O = A
3. (A – B)^t = A^t – B^t 

Determinan Matriks

Apakah Sobat Pintar pernah mendengar istilah determinan dan invers sebelumnya? Kalau belum, berarti inilah saat yang tepat untuk mengetahui apa itu determinan dan invers matriks.

Determinan suatu matriks didefinisikan sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat ditentukan pada matriks persegi. Determinan dari matriks A dapat dituliskan det(A) atau |A|.

Berikut ini sifat-sifat dari determinan matriks:

1. Nilai determinan matriks tidak berubah apabila baris dan kolomnya saling ditukar.
2. Jika semua elemen pada salah satu baris atau kolom sebuah matriks adalah nol, maka determinannya sama dengan nol.
3. Jika dua baris atau dua kolom dari sebuah matriks ditukar, maka tanda determinannya akan berubah.
4. Jika dua baris atau dua kolom dari sebuah matriks elemennya sama atau merupakan kelipatannya, maka determinannya sama dengan nol.
5. Jika setiap elemen pada baris atau kolom dikali oleh bilangan real k, maka determinannya bernilai k kali determinan matriks awal.
6. Jika masing-masing elemen pada baris atau kolom dinyatakan sebagai jumlah dua suku, maka determinan matriks tersebut merupakan jumlah kedua determinan.
7. Nilai sebuah determinan tidak berubah apabila masing-masing elemen pada baris atau kolom dikali dengan bilangan real k dan ditambahkan pada sebarang baris atau kolom.

Determinan Matriks Ordo 2x2

Determinan matriks persegi dengan ordo 2x2 dapat dihitung dengan cara berikut:

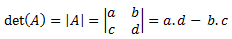
Determinan Matriks Ordo 3x3

Diketahui matriks A dengan ordo 3x3 sebagai berikut:

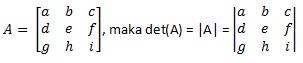
Determinan matriks persegi dengan ordo 3x3 dapat dicari dengan menggunakan 2 cara, yaitu:

Kaidah Sarrus

Langkah-langkah mencari determinan matriks ordo 3x3 dengan kaidah Sarrus:

1. Meletakkan kolom pertama dan kolom kedua di sebelah kanan garis vertikal determinan
2. Jumlahkan hasil kali elemen-elemen yang terletak pada diagonal utama dengan hasil kali elemen-elemen yang sejajar diagonal utama pada arah kanan kemudian kurangi dengan jumlah hasil kali elemen-elemen yang terletak pada diagonal samping dengan elemen-elemen yang sejajar dengan diagonal samping

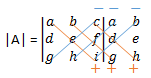
|A| = (a.e.i) + (b.f.g) +( c.d.h) – (c.e.g) – (a.f.h) – (b.d.i)

|A| = (a.e.i + b.f.g + c.d.h) – (c.e.g + a.f.h + b.d.i)

Ekspansi Kofaktor dan Minor

Apabila diketahui sebuah matriks persegi A maka minor elemen a_ij dinyatakan oleh M_ij dan didefinisikan sebagai determinan submatriks yang tinggal setelah baris ke-i dan kolom ke-j dihilangkan dari matriks A

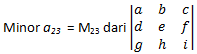
dapat dicari dengan menghilangkan baris kedua dan kolom ketiga sehingga diperoleh:

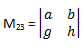
dan nilai determinannya adalah

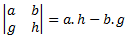
Sedangkan kofaktor dari sebuah elemen adalah nilai minor beserta tandanya. Tanda dari determinan ditentukan dengan memberikan tanda positif (+) pada elemen baris pertama kolom pertama diikuti perubahan tanda ke bawah (vertikal) dan ke kanan (horizontal).

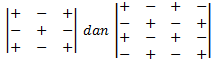
Contoh :

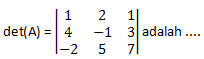
Menggunakan ekspansi kofaktor pada kolom ke 2 diperoleh:

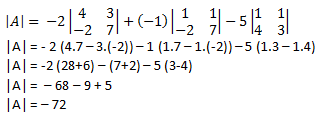
Menyelesaikan Sistem Persamaan Linear dengan Determinan

Menyelesaikan SPLDV dengan Determinan

Loh, kita kan sedang belajar matriks. Kok ada Sistem Persamaan Linear ya?

Eitss.. Kalian belum tahu kalau Sistem Persamaan Linear baik dua variabel ataupun tiga variabel dapat kita selesaikan dengan matriks lho!

Permasalahan SPLDV dapat diselesaikan dengan metode Cramer yaitu menggunakan determinan. 

maka dapat diubah menjadi:

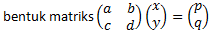
Menyelesaikan SPLTV dengan Determinan