Materi Matematika Wajib - Integral Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo Sobat Pintar, ini nih ada Peta Belajar Bersama materi Matematika bab kedelapan.
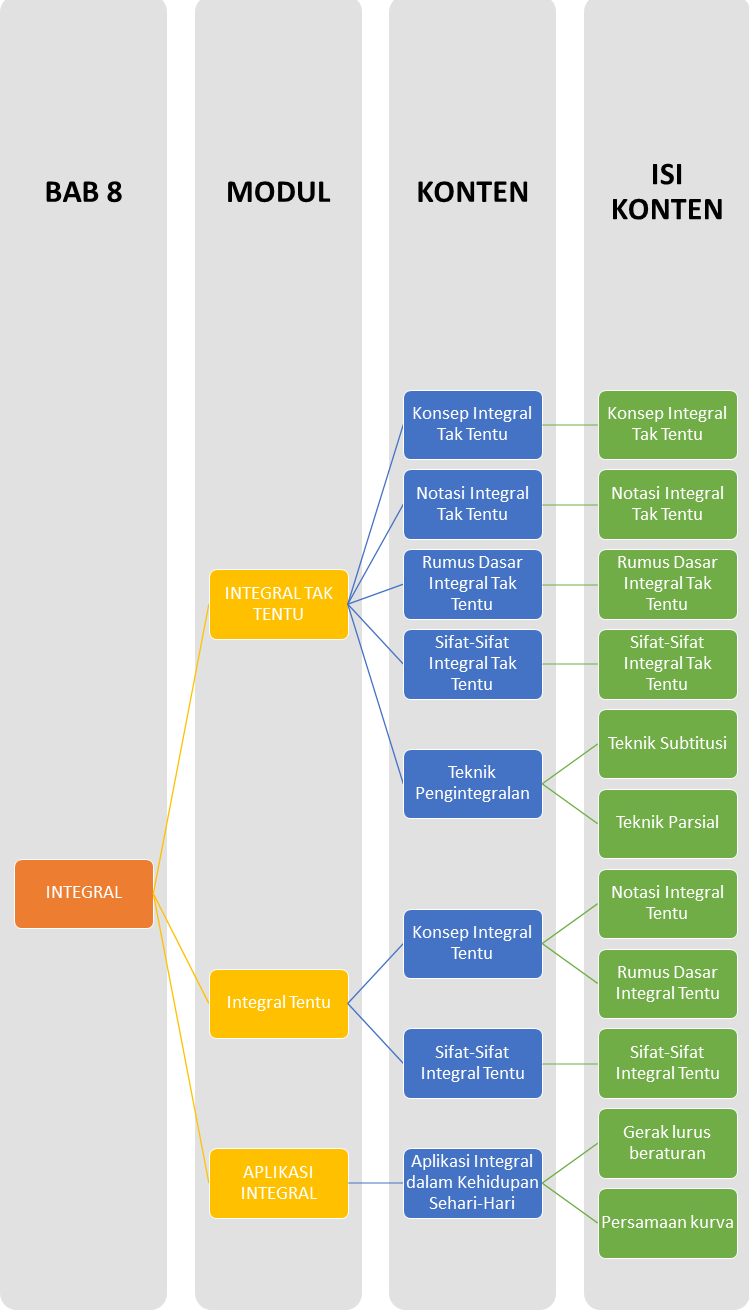
Yuk kita belajar bersama!
Konsep Integral Tak Tentu


Sumber : situsekonomi.com
Sobat Pintar pasti sudah mengetahui luas dari lingkaran, bukan?
Perlu sobat pintar ketahui, bahwa untuk mencari rumus luas lingkaran, kita bisa menggunakan integral lho!
Sebelumnya, apa Sobat Pintar tahu mengenai Integral?
Integral merupakan kebalikan dari turunan fungsi lho, Sobat!
Integral dapat disebut juga dengan antiturunan. Kenapa bisa begitu ya, Sobat?
Karena memang proses menemukan integral suatu fungsi merupakan kebalikan dari proses turunan.

Konsep Integral Tentu

Jika fungsi f terdefinisi pada interval [a,b] maka 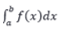 disebut integral tertentu fungsi f dar a ke b. Dimana f(x) disebut integran, a disebut batas bawah, dan b disebut batas atas. Integral Tentu ini memiliki perbedaan dengan integral tak tentu yaitu sudah memiliki nilai tertentu karena sudah ditentukan batasannya.
disebut integral tertentu fungsi f dar a ke b. Dimana f(x) disebut integran, a disebut batas bawah, dan b disebut batas atas. Integral Tentu ini memiliki perbedaan dengan integral tak tentu yaitu sudah memiliki nilai tertentu karena sudah ditentukan batasannya.
Rumus dasar integral tentu :

Aplikasi Integral

Kalau salah satu aplikasi dari turunan adalah kecepatan dan percepatan, menurut kalian aplikasi dari antiturunan atau integral itu apa, Sobat?
Nah, aplikasi dari integral dalam kehidupan sehari-hari antara lain:
PERSAMAAN GERAK LURUS BERATURAN
Konsep integral tak tentu dapat digunakan dalam menentukan persamaan gerak lurus beraturan, yaitu:
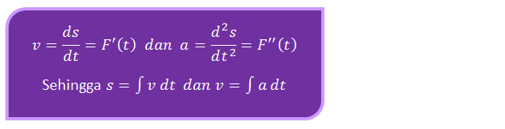
PERSAMAAN KURVA
Diketahui gradien garis singgung dengan kurva y = f(x) adalah m = f’(x), sehingga persamaan kurvanya dapat ditentukan dengan persamaan berikut :

footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








