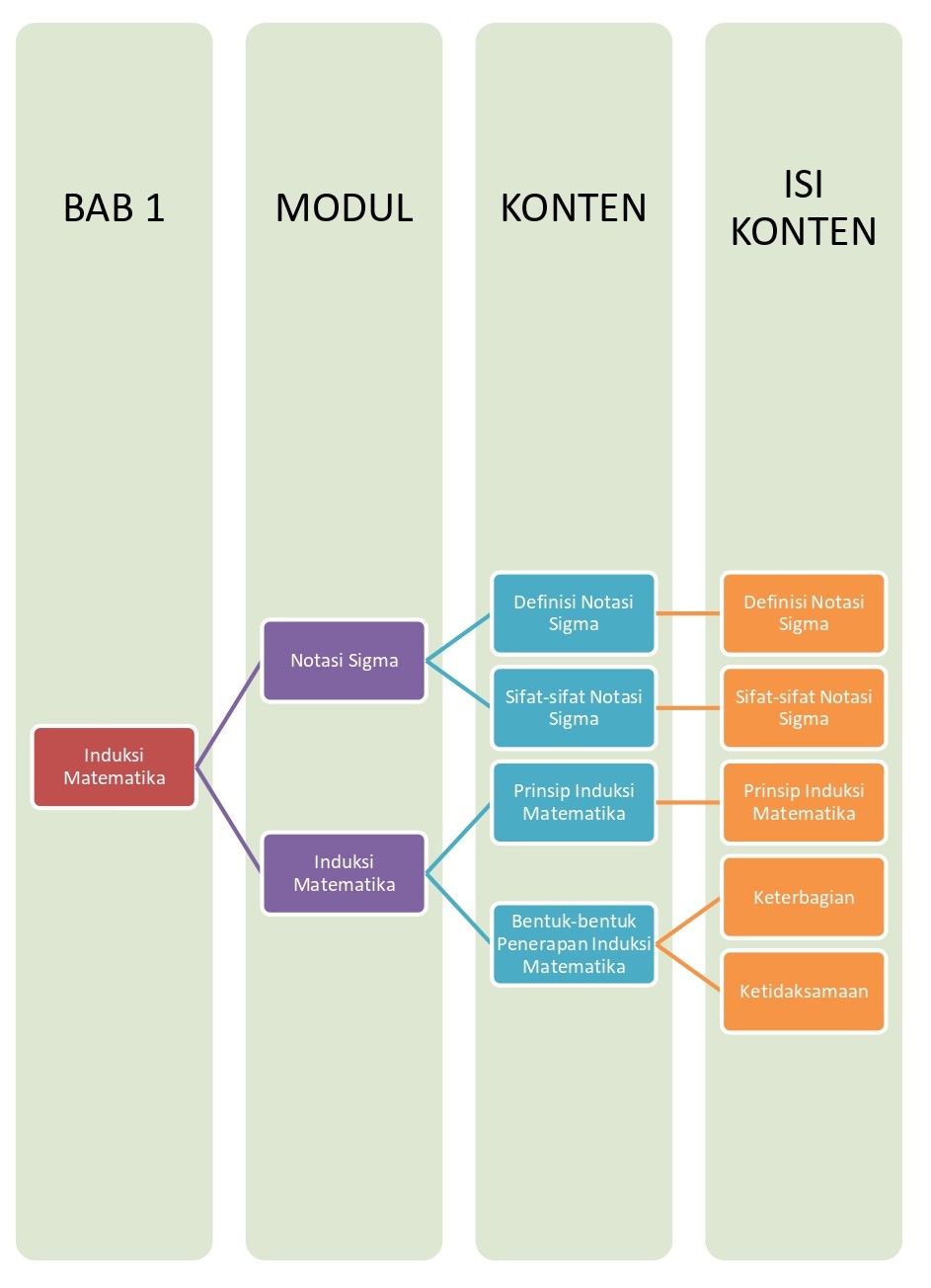
Materi Matematika Wajib - Induksi Matematika Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Notasi Sigma

Sumber : Utusanindo.com
Berapa jumlah siswa dalam kelas kalian, Sobat Pintar?
Apakah jumlahnya sama dengan kelas sebelah atau berbeda? Kalau jumlah seluruh siswa di sekolahmu, berapa Sobat? Pasti banyak sekali! Materi yang akan kita bahas akan berhubungan dengan penjumlahan.
Halo, Sobat Pintar! Kali ini kita akan membahas mengenai notasi sigma. Apa itu notasi sigma?
Notasi sigma merupakan huruf kapital “S” pada bahasa Yunani dari kata “Sum” yang berarti jumlah.

dibaca “Sigma ak dari k = 1 sampai n sama dengan a1 ditambah a2 ditambah a3 dan seterusnya sampai ditambah an”
Keterangan:
a1 = Suku pertama
a2 = Suku kedua, dst
an = Suku ke-n
k=1 merupakan batas bawah notasi sigma
n merupakan batas atas notasi sigma
ak= fungsi yang dijumlahkan dari batas bawah sampai batas atas
Menurut kalian, apa yang akan terjadi jika batas atas atau batas bawahnya digeser?
Jika batas atas k=n digeser menjadi k=n-1 dengan batas bawah tetap k=1, maka banyaknya suku akan berkurang, yaitu terdapat n-1 suku yang dijumlahkan (begitu pula sebaliknya)
Induksi Matematika

Setelah kita mempelajari mengenai notasi sigma, selanjutnya kita akan belajar tentang induksi matematika.
Apakah Sobat Pintar tahu apa itu induksi matematika? Kalau belum tahu, yuk kita belajar bersama!
Induksi matematika merupakan suatu cara pembuktian untuk membuktikan rumus yang memuat variabel dan berlaku untuk setiap bilangan asli. Misalkan P(n) adalah suatu fungsi dalam bilangan bulat positif yang akan dibuktikan kebenarannya untuk setiap n bilangan asli.
Untuk membuktikan fungsi tersebut, kita perlu menunjukkan bahwa :
- P(1) benar (basis Induksi)
- Jika P(n) benar, maka P(n+1) juga benar untuk setiap n bilangan asli, sehingga P(n) bernilai benar ( langkah Induksi)
Implikasi P(n) –> P(n+1) benar untuk setiap bilangan bulat positif dapat ditunjukkan dengan memperlihatkan bahwa berdasarkan hipotesis P(n) benar maka P(n+1) juga harus benar. Langkah pembuktian P(n+1) bernilai benar disebut hipotesis induksi. Secara umum, langkah-langkah dalam induksi matematika dapat dijelaskan sebagai berikut
- Dibuktikan bahwa P(n) benar untuk n=1
- Diasumsikan bahwa P(n) benar untuk n=k
- Akan dibuktikan bahwa P(n) untuk n=k+1
Jika setiap langkah sudah dilakukan dan diuji kebenarannya, maka dapat ditarik kesimpulan bahwa P(n) berlaku untuk setiap n bilangan asli. Prinsip dari induksi matematika dapat diperluas, misalkan P(n) suatu pernyataan yang mana kebenarannya ditentukan oleh nilai n.
Jika P(n) memenuhi dua sifat berikut
- P(n) benar untuk n=m
- untuk setiap bilangan asli k lebih dari sama dengan m, jika P(k) bernilai benar, maka P(k+1) juga bernilai benar, sehingga P(n) bernilai benar untuk semua bilangan asli yang lebih atau sama dengan m
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








