Materi Matematika Wajib - Transformasi Geometri Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo Sobat Pintar, ini nih ada Peta Belajar Bersama materi Matematika bab keempat.
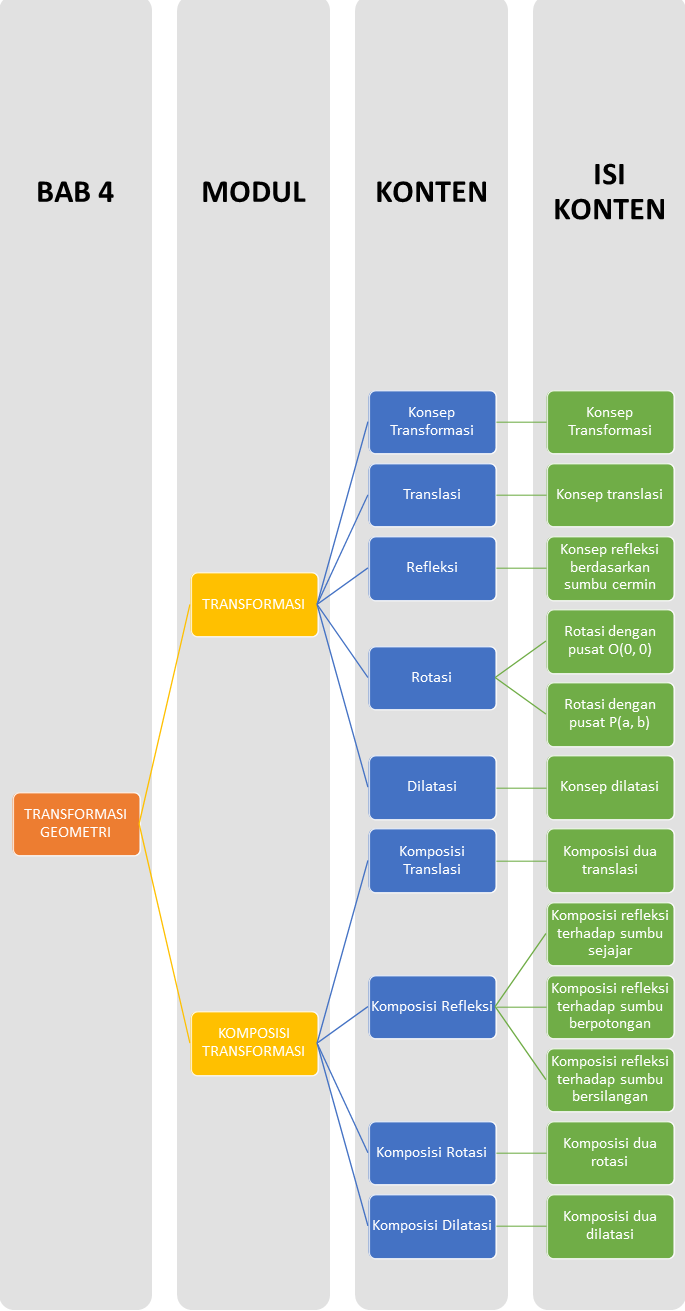
Yuk kita belajar bersama!
Konsep Transformasi


Sumber : Semarangpos.com
Halo Sobat Pintar! Kalian pasti tahu batik, bukan? Apakah kalian pernah mengamati pola pada kain batik yang kalian punya
Apakah kalian menyadari bahwa pola kain batik sebenarnya hanya ada 1 bentuk utama yang kemudian bentuk tersebut digeser atau diperbesar/diperkecil sehingga menghasilkan sebuah pola yang indah. Pembuatan pola batik berhubungan erat dengan transformasi lho!
Yuk, kita belajar bersama mengenai Transformasi!
Transformasi lho yaa.. bukan robot mobil yang suka perang itu, hehe..
Apa itu transformasi?
Transformasi geometri adalah bagian dari geometri yang membahas mengenai perubahan letak maupun bentuk penyajian dari sebuah titik, garis, ataupun bidang. Perlu sobat pintar ketahui, bahwa dalam transformasi terdiri atas:
• Translasi
• Refleksi
• Rotasi
• Dilatasi.
Komposisi Translasi

Berbeda dengan materi sebelumnya yang hanya melewati satu kali transformasi, pada materi kali ini kita akan belajar tentang komposisi transformasi, yaitu hasil dari perubahan letak atau ukuran yang diubah kembali letak atau ukurannya. Komposisi transformasi dilambangkan dengan simbol “o” yang terletak diantara dua transformasi.
Materi komposisi pertama yang akan kita bahas adalah komposisi translasi.
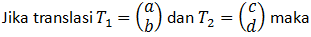
Komposisi dari dua translasi dapat diwakili oleh translasi tunggal
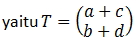
dengan sifat-sifat sebagai berikut:
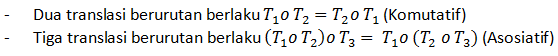
Mudah bukan? Kita lanjut ke komposisi berikutnya, yuk!
Materi Matematika Wajib SMA - 11 MIA Lainnya
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








