Materi Matematika Wajib - Turunan Kelas 11 MIA - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Halo, Sobat Pintar!
Sebelum kita belajar mengenai materi TURUNAN, coba kalian perhatikan Peta Belajar Bersama di bawah ini dulu ya!
Konsep Turunan Fungsi Aljabar


Sumber : androox.com
Sobat pintar pasti sudah sering mendengar istilah kecepatan, bukan?
Perlu kalian tahu nih, Sobat, kalau kecepatan merupakan salah satu aplikasi dari TURUNAN, lho!
Apa itu turunan? Turun dari tangga? Tentu bukan dong, hihi..
Yuk kita belajar bersama mengenai Turunan Fungsi Aljabar
MENENTUKAN GRADIEN GARIS SINGGUNG DENGAN LIMIT
Sebelum kita membahas apa itu turunan serta bagaimana konsepnya, kita akan mengingat materi limit terlebih dahulu, karena
materi turunan berkaitan erat dengan limit suatu fungsi.
Coba perhatikan gambar ini ya, Sobat!
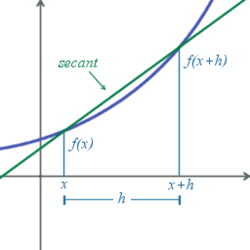
Gradien dari garis sekan yang melalui titik A (x,f(x)) dan titik B(x+h,f(x+h)) dapat dituliskan sebagai berikut:
![]()
Jika nilai x semakin kecil, maka garis akan membentuk garis singgung sehingga diperoleh gradien garis singgungnya di titik A(x,f(x)), yaitu :
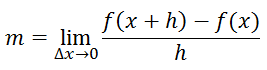
dengan syarat mempunyai limit pada titik tersebut.
Sifat Turunan Fungsi Aljabar

Selain menggunakan definisi turunan dengan limit fungsi, turunan suatu fungsi aljabar juga dapat diselesaikan dengan beberapa aturan berikut.



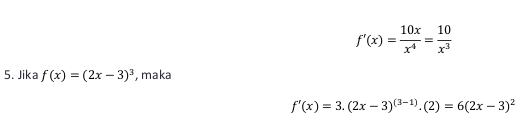
Konsep Kemonotonan Fungsi

Sumber : Jawapos.com
Selain kecepatan, banyak sekali aplikasi dari turunan suatu fungsi lho, Sobat Pintar!
Salah satunya adalah kita dapat menggambarkan kurva yang berbentuk gelombang seperti pada gambar di atas.
Aplikasi turunan yang pertama adalah kemonotonan fungsi, maksudnya kita dapat menentukan suatu fungsi naik atau turun pada suatu interval tertentu.
Konsep kemonotonan fungsi dapat didefinisikan:

Hubungannya dengan turunan suatu fungsi diperlihatkan pada teorema berikut:

footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved








