Materi Matematika - Pola Bilangan Kelas Umum - Belajar Pintar
BelajarPintarV3
Peta Belajar Bersama
Sobat, Ini nih ada Peta Belajar Bersama Matematika di BAB Pertama
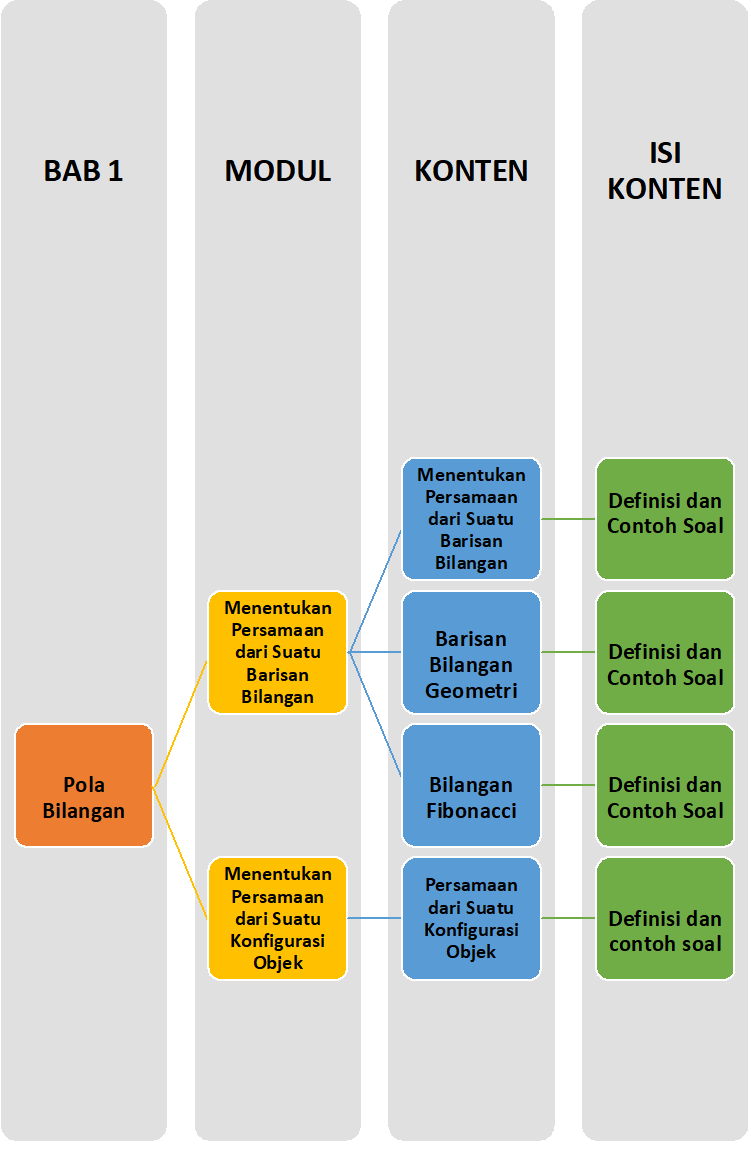
Yuk belajar bersama......
Menentukan Persamaan dari Suatu Barisan Bilangan

Apasih yang dimaksud dengan barisan bilangan? Yuk, Sobat Pintar perhatikan penjelasan dibawah ini.
Barisan bilangan adalah susunan bilangan yang memiliki pola atau aturan tertentu. Untuk menentukan persamaan barisan bilangan, misalnya untuk pola bilangan ganjil yaitu pola bilangan yang terbentuk dari bilangan - bilangan ganjil.
Contoh Soal :
Berikut ini strip dengan tiga warna (merah, putih, biru) seperti yang ditunjukkan pada Gambar dibawah . Pita tersebut diperpanjang dengan pola yang terbentuk.
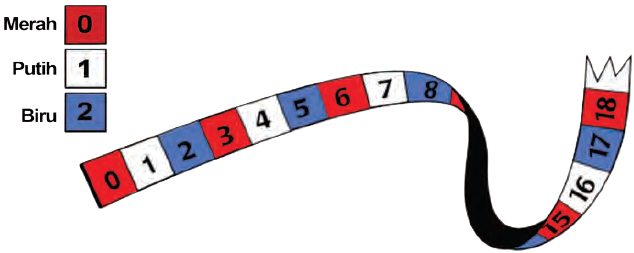
Gambar Pita barisan bilangan tiga warna
Seseorang menyebutkan bilangan 2.345. Dapatkah Sobat Pintar menentukan warna bagian pita bilangan tersebut? Sobat Pintar bisa mengurutkan warna tersebut hingga bertemu dengan urutan ke- 2.345, namun tentu cara tersebut membutuhkan waktu yang lama dan kurang efektif. Sobat Pintar bisa menyelesaikan dengan lebih efektif dengan melihat pola bilangan tersebut.
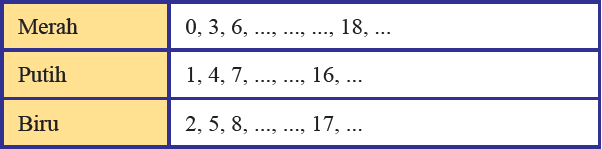
Jika Sobat Pintar kumpulkan sesuai warna bagian pita, Sobat Pintar akan mendapatkan suatu pola. (Isilah titik-titik di tengah pola)
Tabel Barisan bilangan pada pita tiga warna
Jika Sobat Pintar amati, setiap warna tersebut berganti dengan pola yang teratur, yaitu berselisih 3 dengan warna sama terdekat. Pada warna merah, semua bilangannya habis dibagi 3. Sedangkan pada warna putih, semua bilangannya bersisa 1 jika dibagi 3. Kemudian bilangan pada warna biru bersisa 2 jika dibagi 3. Kita rinci barisan bilangan pada pita tiga warna dalam bentuk tabel sebagai berikut.
Tabel Barisan bilangan dengan selisih 3
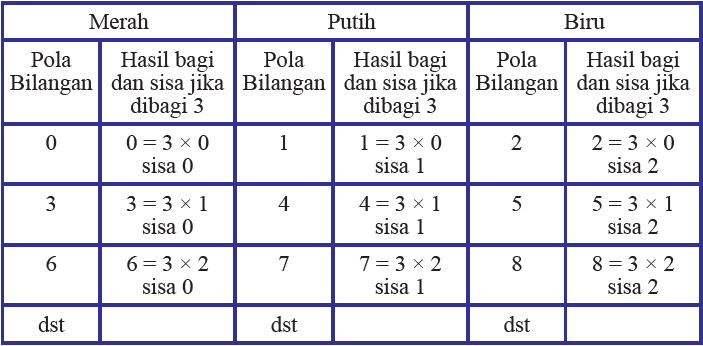
Selanjutnya, kita cek hasil bagi dan sisa jika bilangan 2345 dibagi oleh 3
2.345 = 3 x 781 sisa 2
Perhatikan, sisa pembagiannya adalah 2, yaitu sama dengan sisa pola bilangan pita warna biru. Sehingga dapat kita simpulkan bahwa pita pada urutan ke- 2.345 adalah berwarna biru
Persamaan dari Suatu Konfigurasi Objek

Nah, Sobat Pintar. Berikut ini kalian akan diajak untuk mengamati suatu konfigurasi objek. Setelah mengamati konfigurasi objek tersebut, kalian diajak untuk menggali informasi tentang pola bilangan yang terbentuk, sehingga pada akhirnya kalian bisa membuat persamaan pola bilangan yang kalian temukan.
Contoh Soal :
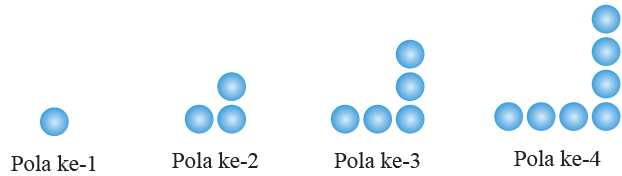
Gambar Pola susunan bola
Dengan memerhatikan pola susunan bola di atas, tentukan:
a. banyak bola pada pola ke-n (Un).
b. jumlah bola hingga pola ke-n (Sn).
Penyelesaian :
a. Pola ke-1: 1 = 2 x 1 - 1
Pola ke-2: 3 = 2 x 2 - 1
Pola ke-3 : 5 = 2 x 3 - 1
Pola ke-4: 7 = 2 x 4 - 1
Dengan memerhatikan pola tersebut, kita bisa simpulkan bahwa
Pola ke-n: Un = 2 x n - 1
b. Perhatikan pola bola-bola yang dijumlahkan pada pola bilangan ganjil. Bola-bola yang dijumlahkan tersebut dapat disusun ulang menjadi bentuk persegi sebagai berikut.
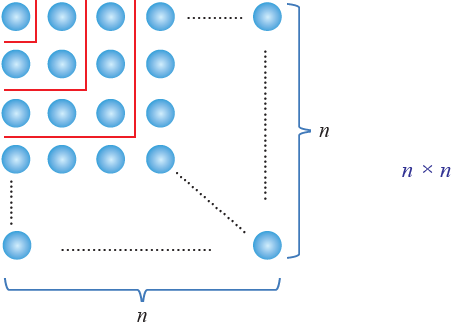
Gambar Pola susunan bola menjadi bentuk persegi
Pola susunan bilangan yang membentuk persegi tersebut dinamakan pola bilangan persegi. Dengan memerhatikan susunan bola tersebut dapat kita simpulkan bahwa penjumlahan hingga pola ke-n adalah
Sn = n2
Dengan kata lain
1 + 3 + 5 + 7 + ... (2 × n - 1) = n2
Materi Matematika Umum - Umum Lainnya

Trigonometri
4 Sub Bab Materi

Fungsi
4 Sub Bab Materi

Sistem Persamaan Linear Dua Variabel
2 Sub Bab Materi

Pola, Barisan, dan Deret
3 Sub Bab Materi

Bidang Kartesius
2 Sub Bab Materi

Perbandingan Bertingkat
1 Sub Bab Materi

Data dan Penyajian Data
3 Sub Bab Materi

Penyajian Data
7 Sub Bab Materi

Segiempat dan Segitiga
8 Sub Bab Materi

Himpunan
4 Sub Bab Materi

Persamaan dan Fungsi Kuadrat
4 Sub Bab Materi

Kekongruenan dan Kesebangunan
3 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







