Materi Matematika - Trigonometri Kelas Umum - Belajar Pintar
BelajarPintarV3
Ukuran Sudut

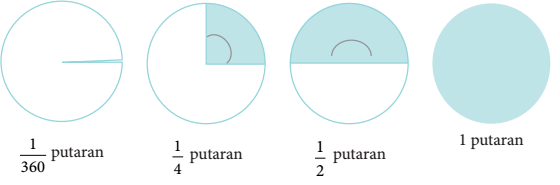
Sebelum Sobatpintar memahami hubungan derajat dengan radian, mari pelajari teori mengenai radian berikut.
Satu radian diartikan sebagai besar ukuran sudut pusat  yang panjang busurnya sama dengan jari-jari
yang panjang busurnya sama dengan jari-jari
Jika 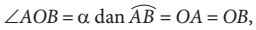 maka
maka 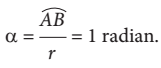
Jika panjang busur tidak sama dengan r, maka cara menentukan besar sudut tersebut dalam satuan radian dapat dihitung menggunakan perbandingan:
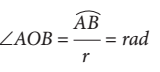
Lebih lanjut, dapat dikatakan bahwa hubungan satuan derajat dengan satuan radian, adalah 1 putaran sama dengan 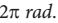 Oleh karena itu, berlaku
Oleh karena itu, berlaku
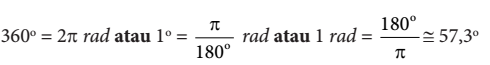
seinggadapat disimpulkan :

bagaimana sobat pintar,udah sekali bukan?
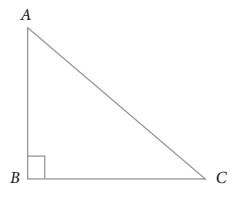
Aturan perbandingan
Hubungan perbandingan sudut (lancip) dengan panjang sisi-sisi suatu segitiga siku-siku dinyatakan dalam definisi berikut.
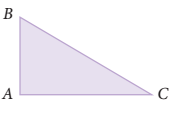
1. Sinus C didefinisikan sebagai perbandingan panjang sisi di depan sudut dengan sisi miring segitiga, ditulis

2. Cosinus C didefinisikan sebagai perbandingan panjang sisi di samping sudut dengan sisi miring segitiga

3. Tangen C didefinisikan sebagai perbandingan panjang sisi di depan sudut dengan sisi di samping sudut, ditulis

4. Cosecan C didefinisikan sebagai perbandingan panjang sisi miring segitiga dengan sisi di depan sudut, ditulis
 atau
atau 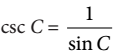
5. Secan C didefinisikan sebagai perbandingan panjang sisi miring segitiga dengan sisi di samping sudut, ditulis
 atau
atau 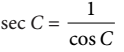
6. Cotangen C didefinisikan sebagai perbandingan sisi di samping sudut dengan sisi di depan sudut, ditulis
 atau
atau 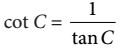
Relasi 2 Sudut Lancip
Untuk memudahkan sobat pintar menyelidiki relasi nilai perbandingan trigonometri tersebut, perhatikan gambar dan penjelasan berikut ini
karena 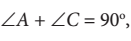 sehingga
sehingga 
sehingga dapat diperoleh
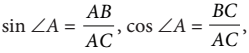
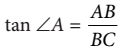
selain itu, sobat pintar juga dapat menuliskan
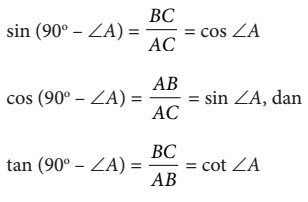
Relasi dua sudut yang lancip dapat dituliskan sebagai berikut

Kemudian jika relasi sudut  pada kuadaran II, dapat ditulis
pada kuadaran II, dapat ditulis
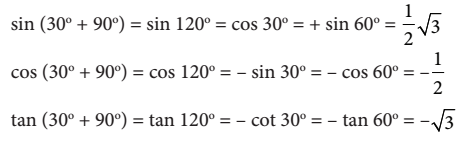
Kemudian jika relasi sudut  pada kuadran III, dapat ditulis
pada kuadran III, dapat ditulis
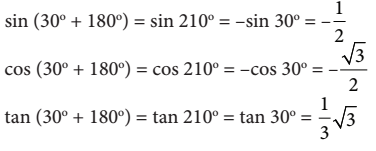
Jika relasi sudut  pada kuadran IV, dapat ditulis
pada kuadran IV, dapat ditulis

Jika relasi sudut  pada kuadran I, dapat ditulis
pada kuadran I, dapat ditulis
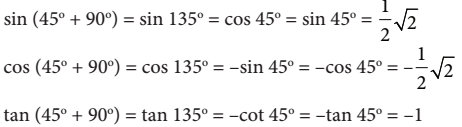
jika relasi sudut  pada kuadran III, dapat ditulis
pada kuadran III, dapat ditulis
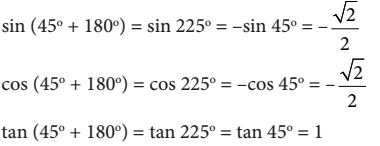
Dengan demikian, diperoleh bahwa
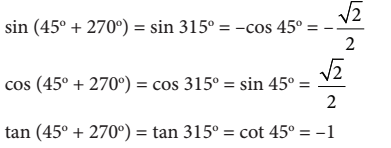
Untuk  dengan cara yang sama dapat diperoleh kesimpulan bahwa
dengan cara yang sama dapat diperoleh kesimpulan bahwa
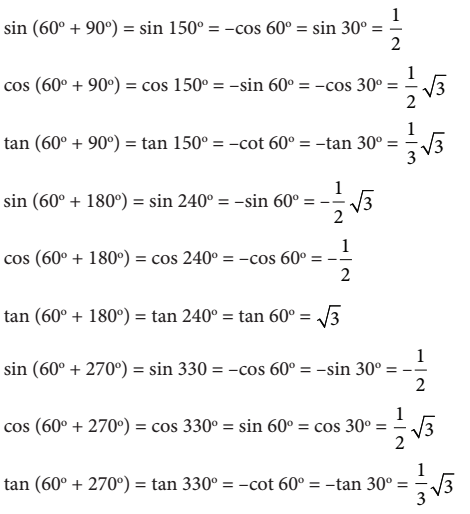
Aturan Sinus
Aturan sinus adalah sebuah aturan yang diturunkan berdasarkan hubungan perbandingan nilai sin dari suatu sudut dengan panjang sisi-sisi pada segitiga. Aturan sinus memperlihatkan perbandingan panjang sisi dengan sinus sudut yang berhadapan dengan sisi tersebut. Dimana aturan sinus ini berlaku pada segitiga lancip dan segitiga tumpul.
1. Penggunaan Aturan Sinus
Menurut aturan sinus, dalam setiap segitiga ABC, perbandingan panjang sisi dengan sinus sudut yang berhadapan dengan sisi tersebut mempunyai nilai yang sama.
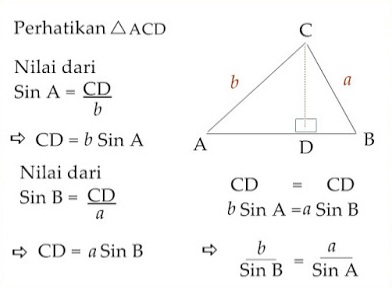
Sehingga untuk segitiga sembarang berlaku Aturan Sinus sebagai berikut :
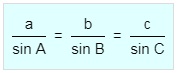
Keterangan :
a = panjang sisi a
A = besar sudut di hadapan sisi a
b = panjang sisi b
B = besar sudut di hadapan sisi b
c = panjang sisi c
C = besar sudut di hadapan sisi c
Contoh soal :
Diketahui segitiga ABC dengan besar <A = 37o, <B = 53o. Jika diketahui panjang sisi b = 10 cm, tentukanlah :
a. Besar <B
b. Panjang sisi a dan sisi c
Jawab :
Karena jumlah total sudut dalam segitiga adalah 180o, maka berlaku :
<A + <B + <C = 180o
<B = 180o - ( <A + <B )
<B = 180o - (37o + 53o)
<B = 180o - 90o
<B = 90o
berdasarkan aturan sinus, maka berlaku :

berdasarkan aturan sinus juga berlaku :

jadi panjang a = 6 cm dan panjang c = 8 cm.
Materi Matematika Umum - Umum Lainnya

Fungsi
4 Sub Bab Materi

Sistem Persamaan Linear Dua Variabel
2 Sub Bab Materi

Pola, Barisan, dan Deret
3 Sub Bab Materi

Bidang Kartesius
2 Sub Bab Materi

Perbandingan Bertingkat
1 Sub Bab Materi

Data dan Penyajian Data
3 Sub Bab Materi

Penyajian Data
7 Sub Bab Materi

Segiempat dan Segitiga
8 Sub Bab Materi

Himpunan
4 Sub Bab Materi

Persamaan dan Fungsi Kuadrat
4 Sub Bab Materi

Pola Bilangan
3 Sub Bab Materi

Kekongruenan dan Kesebangunan
3 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







