APSiswaNavbarV2

redesain-navbar Portlet

BelajarPintarV3

Pola Bilangan

Pola bilangan sendiri memiliki arti suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola . Dan pola bilanga juga memiliki banyak jenisnya atau macamnya .

A. Pola Bilangan Ganjil

Bilangan 1, 3, 5, 7, ... adalah susunan bilangan yang memiliki suatu pola yang dinamakan dengan pola bilangan ganjil. Urutan pertama adalah 1, urutan kedua adalah 3, urutan ketiga adalah 5, dan seterusnya. Bilangan berikutnya diperoleh dengan menambahkan 2 pada bilangan sebelumnya.

B. Pola Bilangan Genap

Bilangan 2, 4, 6, 8, ... adalah susunan bilangan yang memiliki suatu pola yang dinamakan dengan pola bilangan genap. Urutan pertama adalah 2, urutan kedua adalah 4, urutan ketiga adalah 6, dan seterusnya. Bilangan berikutnya diperoleh dengan menambahkan 2 pada bilangan sebelumnya.

C. Pola Bilangan Segitiga

Bilangan 1, 3, 6, 10, ... adalh susunan bilangan yang memiliki suatu pola yang dinamakan dengan pola bilangan segitiga. Urutan pertama adalah 1, urutan kedua adalah 3, urutan ketiga adalah 6, dan seterusnya. Bilangan-bilangan tersebut berasal dari penjumlahan bilangan cacah, yaitu 0 +1 = 1, 0 + 1 + 2 = 3, 0 + 1 + 2 + 3 = 6, dan seterusnya

D. Pola Bilangan Persegi

Bilangan 1, 4, 9, 16, … adalah susunan bilangan yang memiliki suatu pola yang dinamakan dengan pola bilangan persegi. Urutan pertama adalah 1, urutan kedua adalah 4, urutan ketiga adalah 9, dan seterusnya.Pola bilangan tersebut dinamakan pola bilangan persegi atau disebut juga pola bilangan kuadrat, karena untuk mendapatkannya berasal dari kuadrat bilangan asli, yaitu 12 = 1, 22 = 2 32 = 9, dan seterusnya

E. Pola Bilangan Persegi Panjang

Bilangan 2, 6, 12, 20, … adalah susunan bilangan yang memiliki suatu pola yang dinamakan dengan pola bilangan persegi panjang. Urutan pertama adalah 2, urutan kedua adalah 6, urutan ketiga adalah 12, dan seterusnya. Bilangan-bilangan tersebut diperoleh dengan cara mengalikan bilangan yang menunjukan baris dengan bilangan yang menunjukkan kolom sebagai berikut:

Aturannya adalah bilangan yang menunjukkan kolom nilainya selalu satu lebih banyak dari bilangan yang menunjukkan baris

F. Pola Bilangan Segitiga Pascal

Bilangan-bilangan pada segitiga Pascal memiliki suatu pola tertentu, yaitu apabila dua bilangan yang saling berdekatan dijumlahkan, maka akan menghasilkan bilangan-bilangan pada baris selanjutnya, kecuali 1. Sedangkan hasil penjumlahan bilangan pada tiap-tiap baris segitiga Pascal juga memiliki suatu pola dengan rumus 2n – 1, dengan n menunjukkan posisi baris pada segitiga pascal

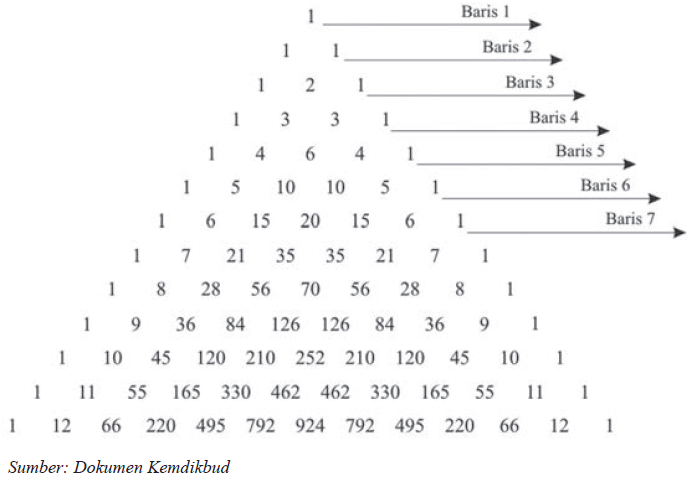
Gambar Segitiga Pascal

Barisan Bilangan

Susunan bilangan yang menyatakan tinggi badan kesepuluh siswa tersebut membentuk suatu barisan bilangan dengan aturan/pola tertentu. Bilangan.bilangan yang terdapat dalam barisan bilangan tersebut dikenal dengan nama suku. Secara umum suku-suku pada barisan bilangan dapat dituliskan sebagai U1, U2, U3, …, Un .

A. Barisan Aritmetika

Coba perhatikan gambar dibawah ini.

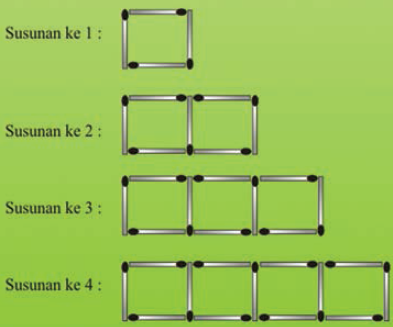
Gambar Susunan batang korek api

Dari gambar diatas diketahui pada susunan ke-1 banyak korek api nya adalah 4, susunan ke-2 sebanyak 7, dan seterusnya. Suku-suku pada barisan bilangan tersebut ditulis secara berurutan seperti di bawah ini.

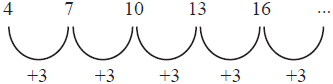
Terlihat bahwa selisih antara dua suku berurutan adalah 3, atau bisa dituiskan sebagai berikut

U2 - U1 = 3

U3 - U2 = 3

U4 - U3 = 3

.

.

.

Un - Un-1 = 3

Suku berikutnya diperoleh dengan cara menambahkan 3 pada suku sebelumnya. Angka 3 ini selanjutnya disebut dengan beda

Pada barisan aritmetika tersebut, diketahui bahwa suku pertama adalah 4, dan beda barisan aritmetika tersebut adalah 3, sehingga rumus suku ke-n adalh Un = 4 + (n-1) x 3.

Barisan bilangan U1, U2, U3, ..., Un disebut barisan aritmetika jika selisih antara dua suku yang berurutan selalu tetap. Selisih antara dua suku yang berurutan disebut dengan beda.

Secara umum, suatu barisan aritmetika dengan suku pertama U1 = a, dan beda antara dua suku yang berurutan adalah b, maka suku ke-n barisan aritmetika tersebut adalah Un = a + (n - 1) x b

B. Barisan Geometri

Coba kamu amati jumlah potongan kertas yang ada setiap kali kamu melakukan kegiatan melipat dan menggunting kertas. Setelah melakukan kegiatan ini sebanyak 1 dan 2 kali, diperoleh banyak potongan kertas yang ada masing-masing sebanyak 2 dan 4 dan seterusnya. Maka dapat ditulis potongan 1 = 2, potongan 2 = 4, potongan = 8, dan seterusnya Suku-suku pada barisan bilangan tersebut ditulis secara berurutan seperti di bawah ini.

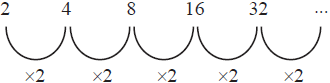
Terlihat bahwa perbandingan antara dua suku berurutan adalah 2, atau bisa dituiskan sebagai berikut:

 

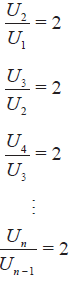
Suku berikutnya diperoleh dengan cara mengalihkan suku sebelumnya dengan 2. Angka 2 ini selanjutnya disebut dengan pembanding/rasio

Pada barisan geometri tersebut, diketahui bahwa suku pertama adalah 2, dan rasio dari barisan geometri tersebut adalah 2, sehingga rumus suku ke-n adalah Un = 2 x 2n-1.

Barisan bilangan U1, U2, U3, ..., Un disebut barisan geometri jika perbandingan antara dua suku yang berurutan selalu tetap. Nilai perbandingan antara dua suku yang berurutan pada barisan geometri disebut dengan pembanding/rasio.

Secara umum, suatu barisan geometri dengan suku pertama U1 = a, dan perbandingan/rasio antara dua suku yang berurutan adalah r, maka suku ke-n barisan aritmetika tersebut adalah Un = a x rn-1

Deret Bilangan

Seperti yang telah dijelaskan pada pembahasan sebelumnya, kita dapat menuliskan suku-suku pada barisan bilangan sebagai U1, U2, U3, ..., Un. Jika suku-suku pada barisan tersebut kita jumlahkan, maka bentuk penjumlahannya disebut dengan deret bilangan, dan dapat dituliskan sebagai U1 + U2 + U3 + ... + Un.

A. Deret Aritmetika

Coba kamu perhatikan tabel dibawah ini.

Tabel Jumlah beberapa suku pertama pada barisan bilangan genap

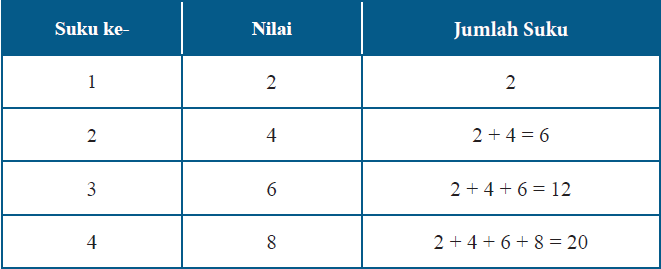
Deret bilangan genap tersebut dapat kita tuliskan dalam bentuk sebagai berikut:

2 + 4 + 6 + 8 + ...

Jika jumlah n suku pertama dinotasikan dengan Sn, maka S4 dari deret di atas adalah

Perhatikan jumlah 4 suku pertama pada deret bilangan genap, yang disimbolkan dengan S4. Angka 2 pada perhitungan tersebut menyatakan suku pertama dari barisan bilangan tersebut, sedangkan angka 8 merupakan suku ke-4. Deret bilangan genap termasuk ke dalam aritmetika.
Secara umun jumlah n suku pertama pada barisan aritmetika adalah:

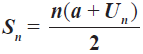
dengan n adalah banyak suku, a adalah suku pertama, dan Un adalah suku ke-n

B. Deret Geometri

Coba kamu perhatikan tabel dibawah ini

Tabel Jumlah kelereng yang dibeli serta total kelerengnya

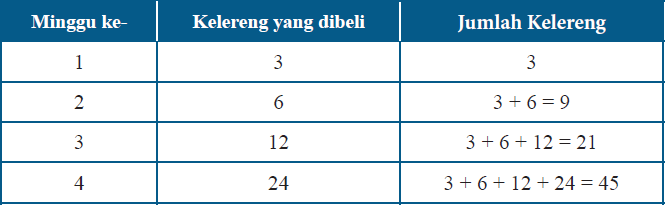
Jumlah dari kelereng pada akhir minggu ke-n dapat dituliskan dalam bentuk deret sebagai berikut:

3 + 6 + 12 + 24 + ...

Deret bilangan tersebut termasuk ke dalam deret geometri. Suku pertama dari deret tersebut adalah 3, dan rasionya adalah 2. Jika jumlah n suku pertama dinotasikan dengan Sn, maka S5 dari deret diatas adalah:

S5 = 3 + 6 + 12 + 24 + 48      (i)

Berikutnya kalikan (i) dengan 2 pada masing-masing ruas sehingga kita peroleh hasil sebagai berikut:

2S5 = 6 + 12 + 24 + 48 + 96      (ii)

Selanjutnya kurangkan (ii) terhadap (i) sehingga didapatkan :

2S5 = 6 + 12 + 24 + 48 + 96
S5 = 3 + 6 + 12 + 24 + 48

2S5 - S5 = 96-3

S5 (2-1) = 3 x 25 - 3
S5 (2-1) = 3 x (25 - 1)
S5 =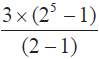

Perhatikan jumlah 5 suku pertama pada deret bilangan diatas, yang disimbolkan dengan S5. Angka 3 di bagian depan dari pembilang pada perhitungan tersebut merupakan suku pertama deret geometri, sedangkan angka 2 pada perpangkatan di dalam tanda kurung dan pada penyebut merupakan rasio dari deret geometri tersebut. Angka 5 menunjukkan penjumlahan pada 5 suku pertama.
Secara umum jumlah n suku pertama pada barisan geometri adalah:

dengan n adalah banyak suku, a adalah suku pertama, dan r adalah rasio dari deret geometri.

Materi Matematika Umum - Umum Lainnya

redesain-navbar Portlet