Materi Matematika - Kekongruenan dan Kesebangunan Kelas Umum - Belajar Pintar
BelajarPintarV3
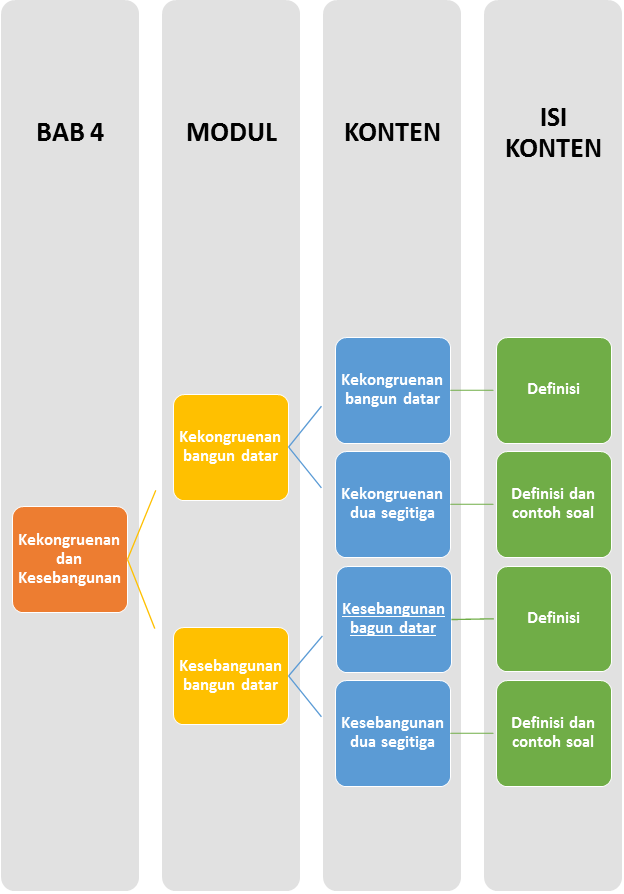
Peta Belajar Bersama
Halo, Sobat!
Sebelum kita belajar tentang Kekongruenan dan Kesebangunan, coba kalian perhatikan Peta Belajar Bersama ini dulu, ya!
Kekongruenan Bangun Datar

Kongruen adalah keadaan dimana dua bangun datar memiliki ukuran yang sama dan dikatakan sebangun.
Dari pengertian tersebut dapat diketahui bahwa semua bangun datar yang kongruen sudah pasti sebangun, namun bangun datar yang sebangun belum tentu kongruen.
Jadi, ciri-ciri bangun datar yang kongruen adalah :
– Memiliki panjang sisi yang sama.
– Memiliki bentuk yang sama.
– Memiliki besar sudut yang sama.
– Sebangun
Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu :
(i) sisi-sisi yang bersesuaian sama panjang
(ii) sudut-sudut yang bersesuaian sama besar
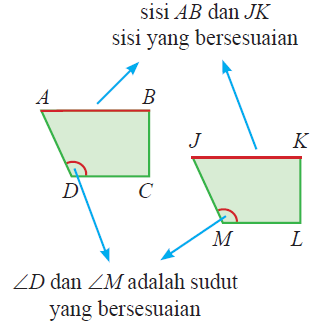
Sudut-sudut yang bersesuaian:
sudut A dan sudut J ---> sudut A = sudut J
sudut B dan sudut K ---> sudut B = sudut K
sudut C dan sudut M ---> sudut D = sudut M
Sisi-sisi yang bersesuaian:
AB dan JK ---> AB = JK
BC dan KL ---> BC = KL
CD dan LM ---> CD = LM
DA dan MJ ---> DA = MJ
Jika bangun ABCD dan JKLM memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ![]()
Jika bangun ABCD dan JKLM tidak memenuhi kedua syarat tersebut, maka bangun ABCD dan JKLM kongruen, dinotasikan dengan ![]()
Catatan:
Ketika menyatakan dua bangun sebangun dinyatakan berdasarkan titik-titik sudut yang bersesuaian dan berurutan, contohnya:
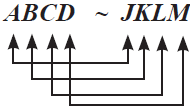 atau
atau 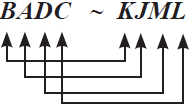 atau
atau 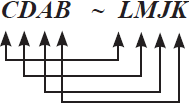
Kesebangunan Bangun Datar

Kesebangunan bangun datar digunakan untuk membandingkan dua buah bangun datar (atau lebih) dengan bentuk yang sama. Dua buah bangun datar dapat dikatakan sebangun apabila panjang setiap sisi pada kedua bangun datar tersebut memiliki nilai perbandingan yang sama.
Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan.
Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat:
(i) perbandingan panjang sisi yang bersesuaian senilai
![]()
(ii) sudut yang bersesuaian besarnya sama
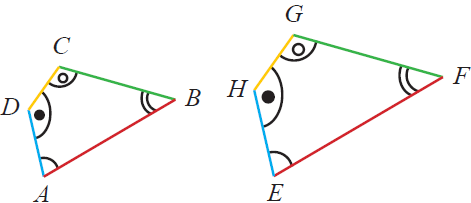
sudut mA = sudut mE
sudut mB = sudut mF
sudut mC = sudut mG
sudut mD = sudut mH
Jika bangun ABC dan DEF memenuhi kedua syarat tersebut, maka bangun ABCD dan EFGH sebangun, dinotasikan dengan ![]()
Jika bangun ABC dan DEF tidak memenuhi kedua syarat tersebut, maka bangun ABCD dan EFGH tidak sebangun, dinotasikan dengan ![]()
Catatan:
Ketika menyatakan dua bangun kongruen sebaiknya dinyatakan berdasarkan titik-titik sudut yang bersesuaian dan berurutan, contohnya:
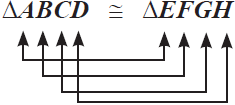 atau
atau 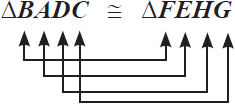 atau
atau 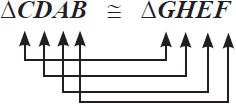
Materi Matematika Umum - Umum Lainnya

Trigonometri
4 Sub Bab Materi

Fungsi
4 Sub Bab Materi

Sistem Persamaan Linear Dua Variabel
2 Sub Bab Materi

Pola, Barisan, dan Deret
3 Sub Bab Materi

Bidang Kartesius
2 Sub Bab Materi

Perbandingan Bertingkat
1 Sub Bab Materi

Data dan Penyajian Data
3 Sub Bab Materi

Penyajian Data
7 Sub Bab Materi

Segiempat dan Segitiga
8 Sub Bab Materi

Himpunan
4 Sub Bab Materi

Persamaan dan Fungsi Kuadrat
4 Sub Bab Materi

Pola Bilangan
3 Sub Bab Materi
footer_v3
Bersama Aku Pintar temukan jurusan kuliah yang tepat
sesuai minat dan bakatmu.
Aku Pintar memiliki visi membuat pendidikan merata, mudah dijangkau, dan terjangkau dengan Program Journey Pintar yang merupakan sebuah program persiapan lengkap bagi siswa SMA/SMK/sederajat yang ingin masuk ke perguruan tinggi impiannya.
Kontak Kami
Grand Slipi Tower Lt. 42
Jl. S. Parman Kav 22-24
Jakarta Barat
© 2024 Aku Pintar. All Rights Reserved







