Persamaan dan Fungsi Kuadrat

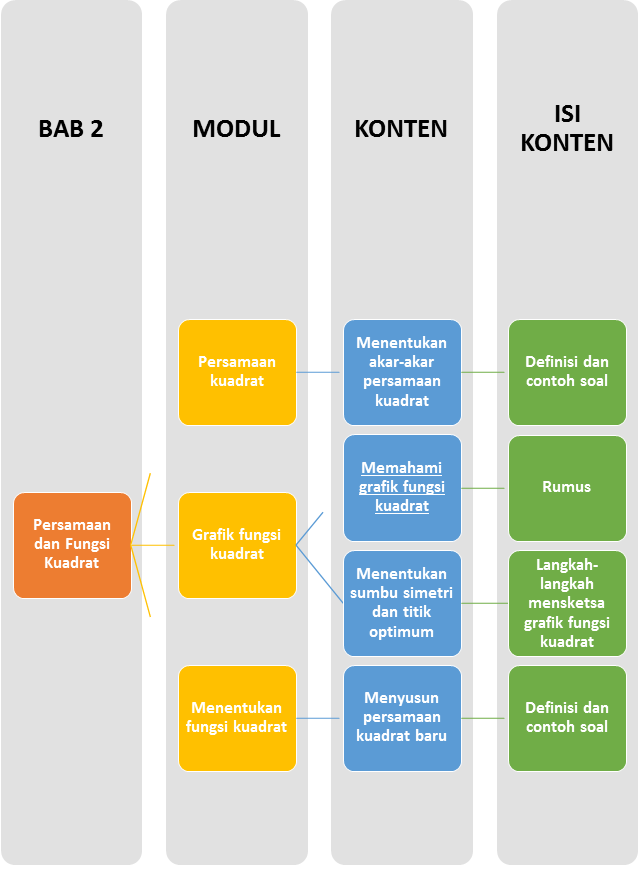
Menentukan Akar-akar Persamaan Kuadrat

Persamaan kuadrat adalah persamaan polinom berderajat dua. Bentuk umum persamaan kuadrat dituliskan sebagai ax² + bx + c = 0 atau dalam bentuk fungsi kuadrat adalah y = ax² + bx + c.

Keterangan:
x = variabel
a = koefisien kuadrat dari x²
b = koefisien linear dari x
c = konstanta

Akar-akar persamaan kuadrat ax² + bx + c = 0 merupakan nilai variabel x sehingga persamaan kuadrat bernilai benar. Akar-akar suatu persamaan kuadrat maskimal ada dua.

Pada grafik fungsi kuadrat, jika x₁ dan x₂ adalah akar-akar persamaan kuadrat, maka titik-titik dengan koordinat (x₁, 0) dan (x₂, 0) merupakan titik potong kurva persamaan kuadrat dengan sumbu x.

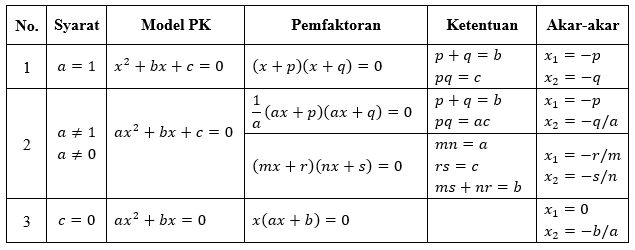
Mencari akar-akar dalam menyelesaikan persamaan kuadrat dilakukan dengan 3 cara sebagai berikut.

1.  Faktorisasi

Faktorisasi atau pemfaktoran merupakan cara mencari akar-akar persamaan kuadrat dengan mencari nilai yang jika dikalikan akan menghasilkan nilai lain. Ada tiga bentuk persamaan kuadrat dengan faktorisasi akar-akar yang berbeda seperti berikut:

 

Contoh Soal :

Tentukan akar-akar persamaan kuadrat x² – 6x + 8 = 0!

Pembahasan :

x² – 6x + 8 = 0
(x – 2)(x – 4) = 0
x – 2 = 0 atau x – 4 = 0
x = 2 x = 4
Jadi, akar-akar persamaan kuadrat x_² – 6x + 8 = 0 adalah x₁ = 2 dan x₂ = 4

2. Kuadrat Sempurna

Tidak semua persamaan kuadrat bisa diselesaikan dengan cara faktorisasi, cara lain untuk menyelesaikan persamaan kuadrat dengan cara melengkapkan kuadrat sempurna.

Bentuk persamaan kuadrat sempurna adalah bentuk persamaan yang menghasilkan bilangan rasional. Penyelesaian persamaan kuadrat dengan melengkapkan kuadrat menggunakan rumus:

(x + p)² = x² + 2px + p²

Ubah menjadi bentuk persamaan dalam (x+p)² = q

Pembahasan :

(x + p)² = q

x + p = + q

x = -p + q

Contoh Soal :

Tentukan akar-akar persamaan kuadrat x² – 6x + 8 = 0!

Pembahasan :

x² – 6x + 8 = 0
x² – 6x = –8
x² – 6x +... = –8 + ...
x² – 6x + 9 = –8 + 9 
(x – 3)² = 1
x – 3) =+ 1
Jika x – 3 = –1       dan jika     x – 3 = 1
                 x = –1 + 3                            x = 1 + 3
                 x = 2                                      x = 4
Jadi, akar-akar persamaan kuadrat x² – 6x + 8 = 0 adalah x₁ = 2 dan x₂ = 4

3. Rumus Kuadrat (Rumus abc)

Selain menggunakan faktorisasi dan dengan melengkapi kuadrat sempurna, persamaan kuadrat dapat diselesaikan dengan menggunakan rumus kuadrat atau biasa dikenal dengan rumus abc.

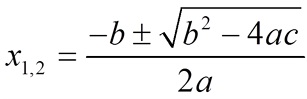
Bentuk b² - 4ac dinamakan dengan Deskriminan (D)

Contoh soal :

Tentukan akar-akar persamaan x² – 6x + 8 = 0!

Pembahasan :

Diketahui a = 1, b = –6, c = 8

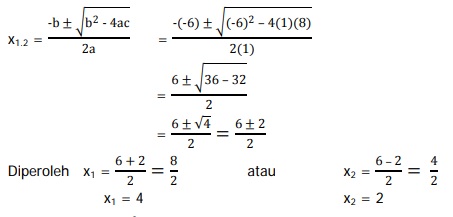
Jadi, akar-akar persamaan kuadrat x² – 6x + 8 = 0 adalah x₁ = 4 dan x₂ = 2

Memahami grafik fungsi kuadrat

Fungsi kuadrat merupakan fungsi yang berbentuk y = ax² + bx + c, dengan a tidak sama dengan 0.

Grafik dari fungsi kuadrat menyerupai parabola, sehingga dapat dikatakan juga sebagai fungsi parabola. 

Berikut merupakan gambar perbandingan grafik fungsi kuadrat y=x² , y = -x², dan y = 2x².

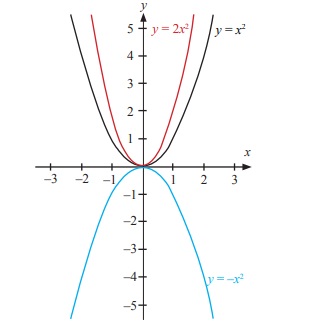
Nilai a pada fungsi y = ax² + bx + c akan mempengaruhi bentuk grafiknya.

Jika a positif maka grafiknya akan terbuka ke atas. Sebaliknya jika a negatif maka grafiknya akan terbuka ke bawah. Jika nilai a semakin besar maka grafiknya menjadi lebih “kurus”.

Berikut merupakan perbandingan grafik fungsi kuadrat y = x² + 2x, y = x² – 3x + 2 dan y = –x² – 5x – 4.

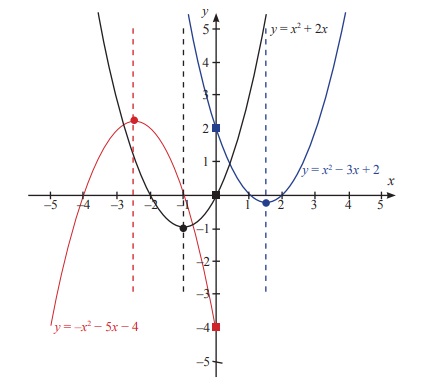
Garis putus-putus pada gambar di atas menerupakan sumbu simetri. Koordinat yang ditandai dengan bulatan merupakan titik puncak sedangkan koordinat yang ditandai dengan persegi merupakan titik potong dengan sumbu-y.

Nilai b pada grafik y = ax² + bx + c menunjukkan letak koordinat titik puncak dan sumbu simetri (titik puncak dan sumbu simetri dibahas lebih lanjut pada subbab selanjutnya).

Jika a > 0, grafik y = ax² + bx + c memiliki titik puncak minimum.

Jika a < 0, grafik y = ax² + bx + c memiliki titik puncak maksimum.

Nilai c pada grafik y = ax² + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu-y, yakni pada koordinat (0, c).

Menyusun Persamaan Kuadrat Baru

Suatu persamaan kuadrat baru dapat dibentuk jika diketahui nilai dari akar-akarnya. Hal tersebut dapat dilakukan dengan memasukan atau mensubstitusi nilai dari akar-akar yang telah diketahui ke dalam persamaan

(x - x₁)(x - x₂)

atau 

x² - (x₁ + x₂) x + (x₁ . x₂)

Suatu persamaan kuadrat baru juga dapat dibentuk walaupun tidak ada diketahui nilai dari akar-akarnya. Dengan syarat, akar-akar tersebut memiliki hubungan atau relasi dengan akar-akar dari persamaan kuadrat yang lain.

Berikut merupakan hubungan akar-akar dari persamaan kuadrat.

x₁ + x₂ = - ^b/a

x₁ . x₂ = ^c/a